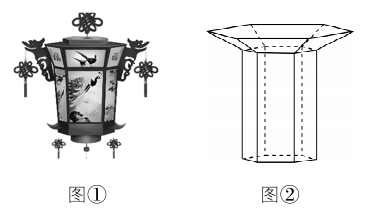
7.如图①所示,宫灯又称宫廷花灯,是中国传统手工艺品之一.图②是小明为自家设计的一个花灯的示意图,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为 $ 4\mathrm{d}\mathrm{m} $ 和 $ 2\mathrm{d}\mathrm{m} $ ,正六棱台与正六棱柱的高分别为 $ 1\mathrm{d}\mathrm{m} $ 和 $ 6\mathrm{d}\mathrm{m} $ ,则该花灯的表面积为( )
解析:正六棱柱的六个侧面面积之和为 $ 2×6×6=72({\mathrm{d}\mathrm{m}}^{2}) $ ,正六棱柱的底面面积为 $ \dfrac{\sqrt{3}}{4}×{2}^{2}×6=6\sqrt{3}({\mathrm{d}\mathrm{m}}^{2}) $ .
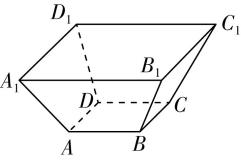
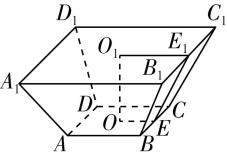
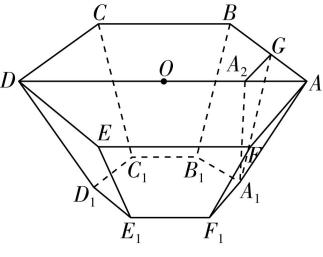
如图所示,正六棱台 $ ABCDEF-{A}_{1}{B}_{1}{C}_{1}{D}_{1}{E}_{1}{F}_{1} $ 中, $ {A}_{1}{B}_{1}=2\mathrm{d}\mathrm{m} $ , $ AB=4\mathrm{d}\mathrm{m} $ .
过点 $ {A}_{1} $ 作 $ {A}_{1}{A}_{2} $ 垂直底面 $ ABCDEF $ 于点 $ {A}_{2} $ ,连接 $ AD $ ,取 $ AD $ 的中点为 $ O $ ,则 $ {A}_{2} $ 为 $ OA $ 的中点,
过点 $ {A}_{2} $ 作 $ {A}_{2}G\perp AB $ 于点 $ G $ ,连接 $ {A}_{1}G $ ,则 $ {A}_{1}G $ 为正六棱台的斜高,
其中 $ {A}_{1}{A}_{2}=1\mathrm{d}\mathrm{m} $ , $ AG=\dfrac{AB-{A}_{1}{B}_{1}}{2}=1\mathrm{d}\mathrm{m} $ , $ A{A}_{2}=\dfrac{1}{2}AO=2\mathrm{d}\mathrm{m} $ ,
由勾股定理得 $ {A}_{2}G=\sqrt{{A}_{2}{A}^{2}-A{G}^{2}}=\sqrt{3}\mathrm{d}\mathrm{m} $ ,故 $ {A}_{1}G=\sqrt{{A}_{2}{G}^{2}+{A}_{1}{\rm A}_{2}^{2}}=2\mathrm{d}\mathrm{m} $ ,
所以正六棱台的斜高为 $ 2\mathrm{d}\mathrm{m} $ ,
故正六棱台的侧面积为 $ \dfrac{1}{2}×(4+2)×2×6=36({\mathrm{d}\mathrm{m}}^{2}) $ .
又正六棱台的下底面 $ ABCDEF $ 的面积为 $ \dfrac{\sqrt{3}}{4}×{4}^{2}×6=24\sqrt{3}({\mathrm{d}\mathrm{m}}^{2}) $ ,
所以该花灯的表面积为 $ 72+6\sqrt{3}+36+24\sqrt{3}=108+30\sqrt{3}({\mathrm{d}\mathrm{m}}^{2}) $ .
故选 $ \mathrm{A} $ .
 (多选)
(多选)