8.3.2 圆柱、圆锥、圆台、球的表面积和体积
一、刷基础
1.已知圆柱的底面直径和高均为2,则该圆柱的侧面积为( )
A. $ 3\mathrm{\pi } $
B. $ 4\mathrm{\pi } $
C. $ 5\mathrm{\pi } $
D. $ 6\mathrm{\pi } $
答案:B
解析:由题意,圆柱的底面半径为1,母线长为2,故圆柱的侧面积为 $ 2\mathrm{\pi }×1×2=4\mathrm{\pi } $ .故选 $ \mathrm{B} $ .
2.已知一个圆柱和一个圆锥的底面半径和高分别相等,圆柱的轴截面是一个正方形,则这个圆柱的侧面积和圆锥的侧面积的比值是( )
A. $ \dfrac{\sqrt{5}}{4} $
B. $ \dfrac{4\sqrt{5}}{5} $
C. $ \dfrac{5}{16} $
D. $ \dfrac{16}{5} $
答案:B
解析:设圆柱和圆锥的底面半径为 $ r $ ,由圆柱的轴截面是一个正方形,得其高 $ h=2r $ ,
则圆柱的侧面积 $ {S}_{1}=2\mathrm{\pi }r×2r=4\mathrm{\pi }{r}^{2} $ ,圆锥的侧面积 $ {S}_{2}=\mathrm{\pi }r\sqrt{(2r)^{2}+{r}^{2}}=\sqrt{5}\mathrm{\pi }{r}^{2} $ ,则 $ \dfrac{{S}_{1}}{{S}_{2}}=\dfrac{4\mathrm{\pi }{r}^{2}}{\sqrt{5}\mathrm{\pi }{r}^{2}}=\dfrac{4\sqrt{5}}{5} $ ,故选 $ \mathrm{B} $ .
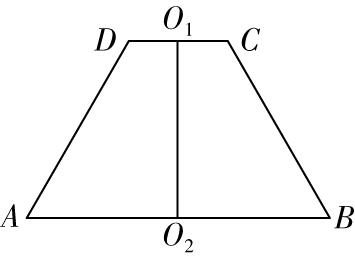
3.已知圆台 $ {O}_{1}{O}_{2} $ 的母线长为4,下底面圆的半径是上底面圆的半径的3倍,轴截面周长为16,则该圆台的表面积为( )
A. $ 24\mathrm{\pi } $
B. $ 25\mathrm{\pi } $
C. $ 26\mathrm{\pi } $
D. $ 27\mathrm{\pi } $
答案:C
解析:如图,作出圆台的轴截面 $ ABCD $ ,设上底面圆 $ {O}_{1} $ 的半径为 $ r $ ,则下底面圆 $ {O}_{2} $ 的半径为 $ 3r $ ,
故轴截面 $ ABCD $ 的周长为 $ 16=4+4+2r+6r $ ,解得 $ r=1 $ ,所以上、下底面圆的面积分别为 $ \mathrm{\pi } $ , $ 9\mathrm{\pi } $ ,圆台侧面积 $ {S}_{侧}=\mathrm{\pi }(1+3)×4=16\mathrm{\pi } $ ,所以圆台的表面积为 $ \mathrm{\pi }+9\mathrm{\pi }+16\mathrm{\pi }=26\mathrm{\pi } $ .故选 $ \mathrm{C} $ .
4.若轴截面为正方形的圆柱的侧面积是 $ S $ ,则圆柱的体积为( )
A. $ \dfrac{S}{2}\sqrt{S} $
B. $ \dfrac{S}{2\mathrm{\pi }}\sqrt{\mathrm{\pi }S} $
C. $ \dfrac{S}{4}\sqrt{S} $
D. $ \dfrac{S}{4\mathrm{\pi }}\sqrt{\mathrm{\pi }S} $
答案:D
解析:设圆柱的高为 $ 2a $ .因为轴截面为正方形,所以底面半径为 $ a $ ,则 $ S=4\mathrm{\pi }{a}^{2} $ ,解得 $ a=\dfrac{\sqrt{\mathrm{\pi }S}}{2\mathrm{\pi }} $ ,故可得圆柱体积 $ V=\mathrm{\pi }{a}^{2}\cdot 2a=2\mathrm{\pi }×\dfrac{S}{4\mathrm{\pi }}×\dfrac{\sqrt{\mathrm{\pi }S}}{2\mathrm{\pi }}=\dfrac{S}{4\mathrm{\pi }}\sqrt{\mathrm{\pi }S} $ .故选 $ \mathrm{D} $ .
5.已知圆锥的表面积为 $ 9\mathrm{\pi } $ ,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A. $ 3\mathrm{\pi } $
B. $ 9\mathrm{\pi } $
C. $ \sqrt{3}\mathrm{\pi } $
D. $ \sqrt{3} $
答案:A
解析:设圆锥的底面半径为 $ r $ ,母线长为 $ l $ ,高为 $ h $ ,
则 $ \begin{cases}\mathrm{\pi }{r}^{2}+\mathrm{\pi }rl=9\mathrm{\pi },\\ \mathrm{\pi }l=2\mathrm{\pi }r,\end{cases} $ 解得 $ \begin{cases}r=\sqrt{3},\\ l=2\sqrt{3}\end{cases} $ (负值舍去),
所以 $ h=\sqrt{{l}^{2}-{r}^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=3 $ ,
所以圆锥的体积 $ V=\dfrac{1}{3}\mathrm{\pi }{r}^{2}h=\dfrac{1}{3}\mathrm{\pi }×(\sqrt{3})^{2}×3=3\mathrm{\pi } $ .故选 $ \mathrm{A} $ .
6.(多选)已知某圆锥的高为2,轴截面面积为4,则( )(多选)
A.该圆锥的母线长为 $ 2\sqrt{2} $
B.该圆锥的体积为 $ 4\mathrm{\pi } $
C.该圆锥的侧面积为 $ 8\sqrt{2}\mathrm{\pi } $
D.与该圆锥同底等高的圆柱的体积为 $ 8\mathrm{\pi } $
答案:AD
解析:设该圆锥的底面半径为 $ r $ ,则轴截面面积为 $ \dfrac{1}{2}×2r×2=4 $ ,解得 $ r=2 $ ,
则该圆锥的母线长为 $ \sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2} $ , $ \mathrm{A} $ 正确;
该圆锥的体积为 $ \dfrac{1}{3}×\mathrm{\pi }{r}^{2}×2=\dfrac{8\mathrm{\pi }}{3} $ , $ \mathrm{B} $ 错误;
该圆锥的侧面积为 $ \mathrm{\pi }×2×2\sqrt{2}=4\sqrt{2}\mathrm{\pi } $ , $ \mathrm{C} $ 错误;
与该圆锥同底等高的圆柱的体积为 $ \mathrm{\pi }{r}^{2}×2=8\mathrm{\pi } $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{D} $ .
7.(多选)折扇是我国古老文化的延续,在我国已有四千年左右的历史,它常以字画的形式体现我国的传统文化(如图①),图②是一个圆台的侧面展开图(扇形的一部分),若两个圆弧 $ \stackrel{⌢}{DE} $ , $ \stackrel{⌢}{AC} $ 所在圆的半径分别是3和6,且 $ \mathrm{\angle }ABC={120}^{\circ } $ ,则下列关于该圆台的说法正确的是( )
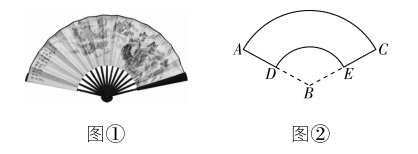 (多选)
(多选)
A.高为 $ 2\sqrt{2} $
B.母线长为3
C.表面积为 $ 14\mathrm{\pi } $
D.体积为 $ \dfrac{16\sqrt{2}}{3}\mathrm{\pi } $
答案:ABC
解析:设圆台的上、下底面半径分别为 $ r $ , $ R $ ,
依题意, $ 2\mathrm{\pi }r=\dfrac{2\mathrm{\pi }}{3}×3 $ ,解得 $ r=1 $ , $ 2\mathrm{\pi }R=\dfrac{2\mathrm{\pi }}{3}×6 $ ,解得 $ R=2 $ ,
又圆台的母线长为 $ l=6-3=3 $ ,
故圆台的高 $ h=\sqrt{{l}^{2}-(R-r)^{2}}=\sqrt{9-1}=2\sqrt{2} $ ,故 $ \mathrm{A} $ , $ \mathrm{B} $ 正确;
圆台的侧面积 $ {S}_{圆台侧}=\mathrm{\pi }×3×(1+2)=9\mathrm{\pi } $ ,
所以圆台的表面积为 $ 9\mathrm{\pi }+\mathrm{\pi }+\mathrm{\pi }×{2}^{2}=14\mathrm{\pi } $ ,故 $ \mathrm{C} $ 正确;
圆台的体积 $ {V}_{圆台}=\dfrac{1}{3}×2\sqrt{2}×\mathrm{\pi }×({1}^{2}+{2}^{2}+1×2)=\dfrac{14\sqrt{2}}{3}\mathrm{\pi } $ ,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
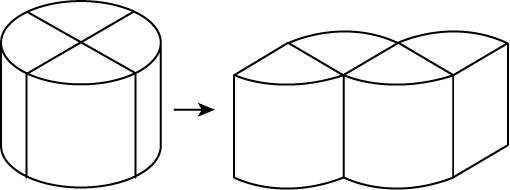
8.如图,将一个圆柱4等分切割,再将其重新组合成一个与圆柱等底等高的几何体,若新几何体的表面积比原圆柱的表面积增加了10,则原圆柱的侧面积是( )
A. $ 10\mathrm{\pi } $
B. $ 20\mathrm{\pi } $
C. $ 100\mathrm{\pi } $
D. $ 200\mathrm{\pi } $
答案:A
解析:设原圆柱的底面圆半径为 $ r $ ,高为 $ h $ ,则原圆柱的表面积为 $ 2\mathrm{\pi }{r}^{2}+2\mathrm{\pi }rh $ ,新几何体的表面积为 $ 2\mathrm{\pi }{r}^{2}+2\mathrm{\pi }rh+2rh $ ,故 $ 2rh=10 $ ,故原圆柱的侧面积为 $ 2\mathrm{\pi }rh=10\mathrm{\pi } $ .故选 $ \mathrm{A} $ .
9.图①为宋代的影青瓷花口盏及盏托,我们不妨将该花口盏及盏托看作是两个圆台与一个圆柱的组合体,三个部分的高相同均为 $ 6\mathrm{c}\mathrm{m} $ ,上面的花口盏是底面直径分别为 $ 8\mathrm{c}\mathrm{m} $ 和 $ 10\mathrm{c}\mathrm{m} $ 的圆台,下面的盏托由底面直径为 $ 8\mathrm{c}\mathrm{m} $ 的圆柱和底面直径分别为 $ 12\mathrm{c}\mathrm{m} $ 和 $ 8\mathrm{c}\mathrm{m} $ 的圆台组合构成,示意图如图②所示,则该花口盏及盏托构成的组合体的体积为( )
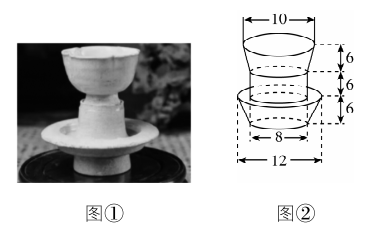
A. $ 248\mathrm{\pi }{\mathrm{c}\mathrm{m}}^{3} $
B. $ 274\mathrm{\pi }{\mathrm{c}\mathrm{m}}^{3} $
C. $ 354\mathrm{\pi }{\mathrm{c}\mathrm{m}}^{3} $
D. $ 370\mathrm{\pi }{\mathrm{c}\mathrm{m}}^{3} $
答案:D
解析:花口盏体积 $ {V}_{1}=\dfrac{1}{3}\mathrm{\pi }×6×({4}^{2}+{5}^{2}+4×5)=122\mathrm{\pi }({\mathrm{c}\mathrm{m}}^{3}) $ ,
盏托体积 $ {V}_{2}=\mathrm{\pi }×{4}^{2}×6+\dfrac{1}{3}\mathrm{\pi }×6×({4}^{2}+{6}^{2}+4×6)=248\mathrm{\pi }({\mathrm{c}\mathrm{m}}^{3}) $ ,
所以组合体的体积 $ V={V}_{1}+{V}_{2}=370\mathrm{\pi }({\mathrm{c}\mathrm{m}}^{3}) $ .
故选 $ \mathrm{D} $ .
10.如图①所示,一个普通的蒙古包可视为一个圆锥与一个圆柱的组合,如图②所示,已知该圆锥的高为2米,圆柱的高为3米,底面直径为6米.

(1) 求该蒙古包的侧面积;
(2) 求该蒙古包的体积.
答案:(1) 【解】依题意得 $ BC=DE=3 $ 米, $ CD=BE=3 $ 米, $ AE=2 $ 米,所以 $ AD=\sqrt{A{E}^{2}+D{E}^{2}}=\sqrt{4+9}=\sqrt{13} $ (米),
所以圆锥的侧面积为 $ \mathrm{\pi }\cdot AD\cdot DE=\mathrm{\pi }×\sqrt{13}×3=3\sqrt{13}\mathrm{\pi } $ (平方米),
圆柱的侧面积为 $ 2\mathrm{\pi }\cdot BC\cdot CD=2\mathrm{\pi }×3×3=18\mathrm{\pi } $ (平方米),
所以该蒙古包的侧面积为 $ (3\sqrt{13}+18)\mathrm{\pi } $ 平方米.
(2) 圆锥的体积为 $ \dfrac{1}{3}\cdot AE\cdot \mathrm{\pi }\cdot D{E}^{2}=\dfrac{1}{3}×2\mathrm{\pi }×{3}^{2}=6\mathrm{\pi } $ (立方米),
圆柱的体积为 $ \mathrm{\pi }\cdot B{C}^{2}\cdot CD=\mathrm{\pi }×{3}^{2}×3=27\mathrm{\pi } $ (立方米),
所以该蒙古包的体积为 $ 6\mathrm{\pi }+27\mathrm{\pi }=33\mathrm{\pi } $ (立方米).
解析:
11.若球的表面积扩大到原来的9倍,那么该球的体积扩大到原来的( )
A.9倍
B.27倍
C.81倍
D.729倍
答案:B
解析:设扩大前后球的半径分别为 $ {r}_{1} $ , $ {r}_{2} $ ,
由表面积之比为 $ \dfrac{4\mathrm{\pi }{r}_{1}^{2}}{4\mathrm{\pi }{r}_{2}^{2}}=\dfrac{{r}_{1}^{2}}{{r}_{2}^{2}}={\left(\dfrac{{r}_{1}}{{r}_{2}}\right) ^ {2}}=\dfrac{1}{9} $ ,得 $ \dfrac{{r}_{1}}{{r}_{2}}=\dfrac{1}{3} $ ,则体积之比为 $ \dfrac{\dfrac{4}{3}\mathrm{\pi }{r}_{2}^{3}}{\dfrac{4}{3}\mathrm{\pi }{r}_{1}^{3}}=\dfrac{{r}_{2}^{3}}{{r}_{1}^{3}}={\left(\dfrac{{r}_{2}}{{r}_{1}}\right) ^ {3}}={3}^{3}=27 $ .故选 $ \mathrm{B} $ .
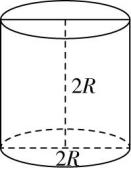
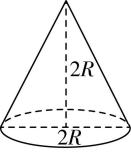
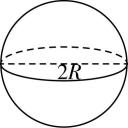
12.(多选)如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径(球的直径为 $ 2R $ )相等,则下列结论正确的是( )
 (多选)
(多选)
A.圆锥的侧面积为 $ 2\mathrm{\pi }{R}^{2} $
B.圆柱与球的表面积之比为 $ 3:2 $
C.圆柱的侧面积与球的表面积相等
D.圆柱、圆锥、球的体积之比为 $ 3:1:2 $
答案:BCD
解析:对于 $ \mathrm{A} $ ,圆锥的母线长 $ l=\sqrt{{\left(2R\right) ^ {2}}+{R}^{2}}=\sqrt{5}R $ ,所以圆锥的侧面积 $ {S}_{1}=\mathrm{\pi }Rl=\sqrt{5}\mathrm{\pi }{R}^{2} $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ \mathrm{C} $ ,圆柱的侧面积 $ {S}_{2}=2\mathrm{\pi }R×2R=4\mathrm{\pi }{R}^{2} $ ,则圆柱的表面积 $ {S}_{3}={S}_{2}+2\mathrm{\pi }{R}^{2}=6\mathrm{\pi }{R}^{2} $ ,
球的表面积 $ {S}_{4}=4\mathrm{\pi }{R}^{2} $ ,所以圆柱与球的表面积之比为 $ 6\mathrm{\pi }{R}^{2}:4\mathrm{\pi }{R}^{2}=3:2 $ ,圆柱的侧面积与球的表面积相等,故 $ \mathrm{B} $ , $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,圆柱的体积 $ {V}_{1}=\mathrm{\pi }{R}^{2}×2R=2\mathrm{\pi }{R}^{3} $ ,圆锥的体积 $ {V}_{2}=\dfrac{1}{3}\mathrm{\pi }{R}^{2}×2R=\dfrac{2}{3}\mathrm{\pi }{R}^{3} $ ,球的体积 $ {V}_{3}=\dfrac{4}{3}\mathrm{\pi }{R}^{3} $ ,所以圆柱、圆锥、球的体积之比为 $ {V}_{1}:{V}_{2}:{V}_{3}=(2\mathrm{\pi }{R}^{3}):(\dfrac{2}{3}\mathrm{\pi }{R}^{3}):(\dfrac{4}{3}\mathrm{\pi }{R}^{3})=3:1:2 $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
13.体积相等的球、正四面体和正方体,它们的表面积的大小关系为( )
A. $ {S}_{球} < {S}_{正四面体} < {S}_{正方体} $
B. $ {S}_{球} < {S}_{正方体} < {S}_{正四面体} $
C. $ {S}_{正四面体} < {S}_{球} < {S}_{正方体} $
D. $ {S}_{正方体} < {S}_{球} < {S}_{正四面体} $
答案:B
解析:设球、正四面体和正方体的体积都为 $ V $ .若球的半径为 $ R $ ,则 $ V=\dfrac{4}{3}\mathrm{\pi }{R}^{3} $ ,可得其表面积 $ {S}_{1}=4\mathrm{\pi }{R}^{2}=\sqrt[3]{36\mathrm{\pi }{V}^{2}} $ .若正四面体的棱长为 $ m $ ,则 $ V=\dfrac{1}{3}\cdot \dfrac{\sqrt{3}}{4}{m}^{2}\cdot \dfrac{\sqrt{6}}{3}m=\dfrac{\sqrt{2}}{12}{m}^{3} $ ,可得 $ m=\sqrt[3]{6\sqrt{2}V} $ ,所以其表面积 $ {S}_{2}=4×\dfrac{\sqrt{3}}{4}{m}^{2}=\sqrt{3}{m}^{2}=\sqrt[3]{216\sqrt{3}{V}^{2}} $ .若正方体的棱长为 $ a $ ,可得 $ V={a}^{3} $ ,所以正方体的表面积 $ {S}_{3}=6{a}^{2}=6\sqrt[3]{{V}^{2}} $ ,可得 $ {S}_{1} < {S}_{3} < {S}_{2} $ ,即 $ {S}_{球} < {S}_{正方体} < {S}_{正四面体} $ .故选 $ \mathrm{B} $ .
14.17世纪30年代,意大利数学家卡瓦列利在《不可分量几何学》一书中介绍了利用平面图形旋转计算球体体积的方法.如图, $ \stackrel{⌢}{AEB} $ 是一个半圆,圆心为 $ O $ , $ ABCD $ 是半圆的外切矩形.以直线 $ OE $ 为轴将该平面图形旋转一周,记 $ △OCD $ 、阴影部分、半圆 $ \stackrel{⌢}{AEB} $ 所形成的几何体的体积分别为 $ {V}_{1} $ , $ {V}_{2} $ , $ {V}_{3} $ ,则下列说法正确的是( )
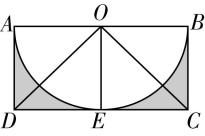
A. $ {V}_{1}+{V}_{2} < {V}_{3} $
B. $ 3{V}_{1}-{V}_{2} > {V}_{3} $
C. $ {V}_{1} > {V}_{2} $
D. $ {V}_{1}={V}_{2} $
答案:D
解析:以直线 $ OE $ 为轴将该平面图形旋转一周, $ △OCD $ 所形成的几何体为一个圆锥,其底面直径为 $ DC=2r(r $ 为半圆半径 $ ) $ ,则 $ {S}_{底}=\mathrm{\pi }{r}^{2} $ , $ h=OE=r $ ,则 $ {V}_{1}=\dfrac{1}{3}{S}_{底}h=\dfrac{1}{3}\mathrm{\pi }{r}^{3} $ .
半圆 $ \stackrel{⌢}{AEB} $ 所形成的几何体为一个半球,设整个球的体积 $ V=\dfrac{4}{3}\mathrm{\pi }{r}^{3} $ ,则 $ {V}_{3}=\dfrac{1}{2}V=\dfrac{2}{3}\mathrm{\pi }{r}^{3} $ .
以直线 $ OE $ 为轴将该平面图形旋转一周,长方形 $ ABCD $ 形成的几何体为圆柱,
设体积为 $ {V}_{4}=Sh=\mathrm{\pi }{r}^{3} $ ,则阴影部分所形成的几何体体积 $ {V}_{2} $ 等于圆柱体体积减去半球体积,则 $ {V}_{2}=\mathrm{\pi }{r}^{3}-\dfrac{2}{3}\mathrm{\pi }{r}^{3}=\dfrac{1}{3}\mathrm{\pi }{r}^{3} $ .
故 $ {V}_{1}={V}_{2} $ , $ {V}_{1}+{V}_{2}={V}_{3} $ , $ 3{V}_{1}-{V}_{2}={V}_{3} $ .故选 $ \mathrm{D} $ .
15.球面被平面所截得的一部分叫做球冠,截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高.球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高,球缺是旋转体,可以看作是球冠和其底所在的圆面所围成的几何体.如图①,一个球面的半径为 $ R $ ,球冠的高是 $ h $ ,球冠的表面积公式是 $ S=2\mathrm{\pi }Rh $ .如图②,已知 $ C $ , $ D $ 是以 $ AB $ 为直径的圆上的两点, $ \mathrm{\angle }AOC=\mathrm{\angle }BOD=\dfrac{\mathrm{\pi }}{3} $ , $ {S}_{扇形COD}=6\mathrm{\pi } $ ,则扇形 $ COD $ 绕直线 $ AB $ 旋转一周形成的几何体的表面积为 .
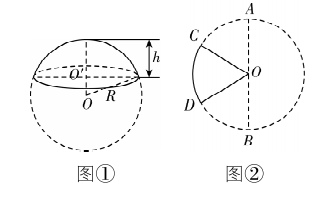
答案: $ 72\mathrm{\pi }+36\sqrt{3}\mathrm{\pi } $
解析:因为 $ \mathrm{\angle }AOC=\mathrm{\angle }BOD=\dfrac{\mathrm{\pi }}{3} $ ,所以 $ \mathrm{\angle }DOC=\mathrm{\pi }-2×\dfrac{\mathrm{\pi }}{3}=\dfrac{\mathrm{\pi }}{3} $ .设圆 $ O $ 的半径为 $ R $ ,又 $ {S}_{扇形COD}=\dfrac{1}{2}×\dfrac{\mathrm{\pi }}{3}{R}^{2}=6\mathrm{\pi } $ ,解得 $ R=6 $ (负值舍去).
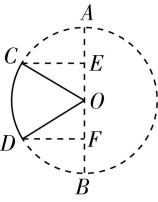
如图,过点 $ C $ 作 $ CE\perp AB $ 交 $ AB $ 于点 $ E $ ,过点 $ D $ 作 $ DF\perp AB $ 交 $ AB $ 于点 $ F $ ,
则 $ CE=OC \sin \dfrac{\mathrm{\pi }}{3}=3\sqrt{3} $ , $ OE=OC \cos \dfrac{\mathrm{\pi }}{3}=3 $ ,所以 $ AE=R-OE=3 $ ,同理可得 $ DF=3\sqrt{3} $ , $ OF=BF=3 $ .
将扇形 $ DOC $ 绕直线 $ AB $ 旋转一周形成的几何体为在一个半径 $ R=6 $ 的球中上下截去两个相同的球冠所剩余部分再挖去两个相同的圆锥,其中球冠的高 $ h=3 $ ,圆锥的高 $ {h}_{1}=3 $ ,底面半径 $ r=3\sqrt{3} $ ,则其中一个球冠的表面积 $ {S}_{1}=2\mathrm{\pi }Rh=2\mathrm{\pi }×6×3=36\mathrm{\pi } $ ,球的表面积 $ {S}_{2}=4\mathrm{\pi }{R}^{2}=4\mathrm{\pi }×{6}^{2}=144\mathrm{\pi } $ ,圆锥的侧面积 $ {S}_{3}=3\sqrt{3}×6\mathrm{\pi }=18\sqrt{3}\mathrm{\pi } $ ,所以所求几何体的表面积 $ S={S}_{2}-2{S}_{1}+2{S}_{3}=144\mathrm{\pi }-2×36\mathrm{\pi }+2×18\sqrt{3}\mathrm{\pi }=72\mathrm{\pi }+36\sqrt{3}\mathrm{\pi } $ .
16.如图,已知在圆锥 $ SO $ 中,底面 $ \odot O $ 的直径 $ AB=12 $ , $ △SAB $ 的面积为48.
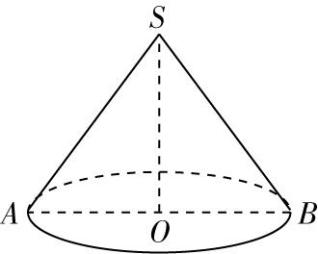
(1) 求圆锥 $ SO $ 的表面积;
(2) 一个球刚好能放进该圆锥体中,求这个球的半径以及此时圆锥体剩余空间的体积.
答案:(1) 【解】设圆锥 $ SO $ 的母线长为 $ l $ ,底面 $ \odot O $ 的直径为 $ 2r $ ,所以 $ 2r=12 $ ,得 $ r=6 $ .
因为 $ △SAB $ 的面积为48,所以 $ {S}_{△SAB}=\dfrac{1}{2}\cdot 2r\cdot SO=48 $ ,解得 $ SO=8 $ .
由勾股定理,可得母线 $ l=\sqrt{S{O}^{2}+{r}^{2}}=10 $ .
由圆锥的表面积公式得 $ {S}_{表}={S}_{侧}+{S}_{底}=\mathrm{\pi }rl+{\mathrm{\pi }r}^{2}=60\mathrm{\pi }+36\mathrm{\pi }=96\mathrm{\pi } $ .
(2) 球与圆锥的侧面相切,如图,作出圆锥的轴截面,设球心为 $ D $ ,球与圆锥轴截面 $ SAB $ 的边 $ SB $ 相切于点 $ E $ ,连接 $ DE $ ,则 $ DE\perp SB $ , $ DE=OD=R $ (其中 $ R $ 为球的半径),
则 $ △SED\sim △SOB $ ,可得 $ DE:BO=SD:SB $ ,即 $ \dfrac{R}{6}=\dfrac{8-R}{10} $ ,解得 $ R=3 $ ,
所以球的体积 $ {V}_{1}=\dfrac{4}{3}\mathrm{\pi }{R}^{3}=36\mathrm{\pi } $ ,圆锥的体积 $ {V}_{2}=\dfrac{1}{3}\mathrm{\pi }{r}^{2}\cdot SO=96\mathrm{\pi } $ ,
故圆锥体剩余空间的体积 $ V={V}_{2}-{V}_{1}=60\mathrm{\pi } $ .

解析:
17.已知长方体的长、宽、高分别为1,1,2,并且其顶点都在球 $ O $ 的球面上,则球 $ O $ 的体积是( )
A. $ \sqrt{2}\mathrm{\pi } $
B. $ \sqrt{6}\mathrm{\pi } $
C. $ 2\sqrt{2}\mathrm{\pi } $
D. $ 6\mathrm{\pi } $
答案:B
解析:长方体的体对角线即为其外接球的直径,
故外接球的半径 $ R=\dfrac{\sqrt{{1}^{2}+{1}^{2}+{2}^{2}}}{2}=\dfrac{\sqrt{6}}{2} $ ,
因此外接球的体积为 $ \dfrac{4\mathrm{\pi }{R}^{3}}{3}=\dfrac{4×6\sqrt{6}}{3×8}\mathrm{\pi }=\sqrt{6}\mathrm{\pi } $ .故选 $ \mathrm{B} $ .
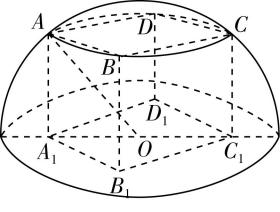
18.已知棱长为4的正方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 的一个面 $ {A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 在一半球的底面上,且 $ A $ , $ B $ , $ C $ , $ D $ 四个顶点都在此半球面上,则此半球的体积为( )
A. $ 32\sqrt{6}\mathrm{\pi } $
B. $ 4\sqrt{6}\mathrm{\pi } $
C. $ 16\sqrt{3}\mathrm{\pi } $
D. $ 8\sqrt{6}\mathrm{\pi } $
答案:A
解析:如图,设半球的球心为 $ O $ ,半径为 $ R $ ,连接 $ OA $ .
由题易知半球的球心是底面正方形 $ {A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 的中心,且 $ O{A}_{1}=\dfrac{\sqrt{2}}{2}×4=2\sqrt{2} $ , $ A{A}_{1}=4. $
在 $ \mathrm{R}\mathrm{t}△OA{A}_{1} $ 中, $ {R}^{2}=O{A}^{2}={4}^{2}+(2\sqrt{2})^{2}=24 $ ,解得 $ R=2\sqrt{6} $ ,
故半球的体积 $ V=\dfrac{1}{2}×\dfrac{4}{3}\mathrm{\pi }(2\sqrt{6})^{3}=32\sqrt{6}\mathrm{\pi } $ ,故选 $ \mathrm{A} $ .
19.已知一个圆锥的顶点和底面的圆周在同一个球面上,若球的体积为 $ 36\mathrm{\pi } $ ,圆锥的体积为 $ \dfrac{5\mathrm{\pi }}{3} $ ,且圆锥的高为正整数,则该圆锥的侧面积为( )
A. $ \sqrt{10}\mathrm{\pi } $
B. $ 2\sqrt{5}\mathrm{\pi } $
C. $ \sqrt{30}\mathrm{\pi } $
D. $ 2\sqrt{10}\mathrm{\pi } $
答案:C
解析:设球的半径为 $ R $ ,则 $ 36\mathrm{\pi }=\dfrac{4}{3}\mathrm{\pi }{R}^{3} $ ,解得 $ R=3 $ .
设圆锥的底面圆半径为 $ r $ ,高为 $ h(h\in {\boldsymbol{N}}^{\ast } $ 且 $ 0 < h < 6) $ .
因为圆锥的体积为 $ \dfrac{5\mathrm{\pi }}{3}=\dfrac{1}{3}\mathrm{\pi }{r}^{2}h $ ,所以 $ h{r}^{2}=5① $ .
又由题意可得, $ (R-h)^{2}+{r}^{2}={R}^{2}② $ ,
由①②解得 $ h=1 $ , $ r=\sqrt{5} $ ,
所以该圆锥的侧面积 $ S=\dfrac{1}{2}\cdot 2\mathrm{\pi }r\sqrt{{r}^{2}+{h}^{2}}=\sqrt{30}\mathrm{\pi } $ .故选 $ \mathrm{C} $ .
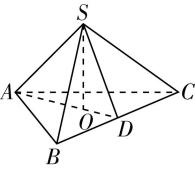
20.某工艺品加工厂收到一块底面棱长为 $ 2\sqrt{3} $ 厘米,侧棱长为 $ 2\sqrt{7} $ 厘米的正三棱锥形状的珍贵木材,现用这块木材制作一个独特的球形饰品,则这个球形饰品的表面积的最大值是( )
A. $ \dfrac{4\mathrm{\pi }}{3} $ 平方厘米
B. $ \dfrac{8\mathrm{\pi }}{3} $ 平方厘米
C. $ 4\mathrm{\pi } $ 平方厘米
D. $ 8\mathrm{\pi } $ 平方厘米
答案:B
解析:如图,设正三棱锥底面的中心为 $ O $ ,在正三棱锥的底面 $ ABC $ 中, $ AB=2\sqrt{3} $ , $ AD=\sqrt{ (2\sqrt{3})^{2}-{\left(\dfrac{2\sqrt{3}}{2} \right) ^ {2}}}=3 $ ,
所以 $ {S}_{△ABC}=\dfrac{1}{2}×2\sqrt{3}×3=3\sqrt{3} $ .
在 $ △SBC $ 中, $ SB=2\sqrt{7} $ , $ SD=\sqrt{ (2\sqrt{7})^{2}-{\left(\dfrac{2\sqrt{3}}{2} \right) ^ {2}}}=5 $ ,所以 $ {S}_{△SBC}=\dfrac{1}{2}×2\sqrt{3}×5=5\sqrt{3} $ .
所以该木材的表面积 $ S={S}_{△ABC}+3{S}_{△SBC}=3\sqrt{3}+3×5\sqrt{3}=18\sqrt{3} $ ,
又 $ AO=\dfrac{2}{3}AD=2 $ ,所以 $ SO=\sqrt{(2\sqrt{7})^{2}-{2}^{2}}=2\sqrt{6} $ ,
所以 $ {V}_{S-ABC}=\dfrac{1}{3}×3\sqrt{3}×2\sqrt{6}=6\sqrt{2} $ .
要使这个球形饰品的表面积最大,则这个球形饰品是该木材的内切球.
设内切球的半径为 $ r $ 厘米,则 $ \dfrac{1}{3}Sr={V}_{S-ABC} $ ,所以 $ r=\dfrac{3{V}_{S-ABC}}{S}=\dfrac{18\sqrt{2}}{18\sqrt{3}}=\dfrac{\sqrt{6}}{3} $ ,
所以内切球的表面积为 $ 4\mathrm{\pi }{r}^{2}=\dfrac{8\mathrm{\pi }}{3} $ ,故这个球形饰品的表面积的最大值为 $ \dfrac{8\mathrm{\pi }}{3} $ 平方厘米.故选 $ \mathrm{B} $ .
21.甲球与某正方体的各个面都相切,乙球与这个正方体的各条棱都相切,丙球过这个正方体的所有顶点,则甲、乙、丙三球的半径的平方之比为( )
A. $ 1:2:3 $
B. $ 1:\sqrt{2}:\sqrt{3} $
C. $ 1:\sqrt[3]{4}:\sqrt[3]{9} $
D. $ 1:2\sqrt{2}:3\sqrt{3} $
答案:A
解析:设正方体的棱长为 $ a $ .
如图①,对于正方体的内切球,取其中截面,则球的直径等于正方体的棱长,即 $ 2{R}_{甲}=a $ ,所以 $ {R}_{甲}=\dfrac{a}{2} $ .
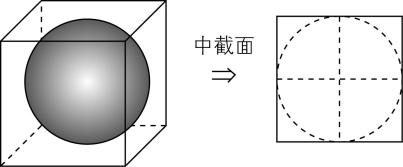
图①
如图②,对于正方体的棱切球,取其中截面,则球的直径等于正方体的面对角线,即 $ 2{R}_{乙}=\sqrt{2}a $ ,所以 $ {R}_{乙}=\dfrac{\sqrt{2}a}{2} $ .
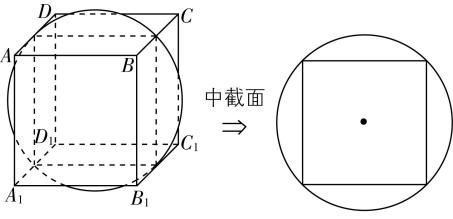
图②
如图③,对于正方体的外接球,取其对角面,则球的直径等于正方体的体对角线,即 $ 2{R}_{丙}=\sqrt{3}a $ ,所以 $ {R}_{丙}=\dfrac{\sqrt{3}a}{2} $ .
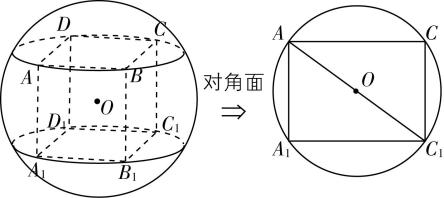
图③
所以甲、乙、丙三球的半径的平方之比为 $ 1:2:3 $ .故选 $ \mathrm{A} $ .
22.水平桌面上放置了4个完全相同的半径为1的小球(不叠起),四个小球的球心构成正方形,且相邻的两个小球相切.用一个半球形容器(容器壁厚度不计)罩住这四个小球,则这个半球形容器表面积(不包含底面圆)的最小值为( )
A. $ (6+4\sqrt{2})\mathrm{\pi } $
B. $ (8+4\sqrt{3})\mathrm{\pi } $
C. $ (3+2\sqrt{2})\mathrm{\pi } $
D. $ (4+2\sqrt{3})\mathrm{\pi } $
答案:B
解析:如图①,4个小球球心构成的正方形为 $ {O}_{1}{O}_{2}{O}_{3}{O}_{4} $ ,中心为 $ N $ .
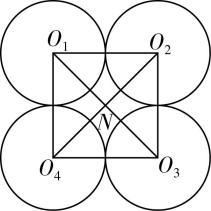
图①
由题意知 $ {O}_{1}{O}_{2}=2 $ , $ N{O}_{1}=\sqrt{2} $ ,设半球形容器的球心为 $ O $ ,显然当半球形容器与4个小球都相切时球 $ O $ 的半径最小.设半球形容器与球 $ {O}_{1} $ 的切点为 $ A $ ,且球心 $ {O}_{1} $ , $ {O}_{2} $ , $ {O}_{3} $ , $ {O}_{4} $ 在半球底面上的射影分别为 $ {A}_{1} $ , $ {B}_{1} $ , $ {C}_{1} $ , $ {D}_{1} $ ,则 $ {O}_{1}{O}_{2}{O}_{3}{O}_{4}-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 为长方体.连接 $ ON $ ,如图②,则 $ ON= $ 小球的半径 $ =1 $ ,
球 $ O $ 的半径 $ =OA={O}_{1}A+O{O}_{1}=1+\sqrt{O{N}^{2}+{O}_{1}{N}^{2}}=1+\sqrt{3} $ ,所以半球形容器表面积(不包含底面圆)的最小值为 $ 2\mathrm{\pi } (1+\sqrt{3})^{2}= (8+4\sqrt{3} )\mathrm{\pi } $ ,故选 $ \mathrm{B} $ .
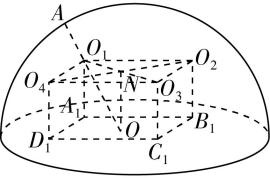
图②
23.已知圆锥的底面圆半径为2,且内切球球心与外接球球心重合,则圆锥外接球的表面积为 .
答案: $ \dfrac{64\mathrm{\pi }}{3} $
解析:如图,作圆锥的轴截面为 $ PAB $ ,由题可知等腰三角形 $ PAB $ 的内切圆与外接圆圆心相同,设为 $ O $ ,所以 $ △PAB $ 为等边三角形.
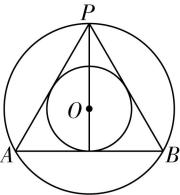
又 $ AB=4 $ ,所以 $ OP=\dfrac{2}{3}×4×\dfrac{\sqrt{3}}{2}=\dfrac{4\sqrt{3}}{3} $ ,即圆锥外接球的半径为 $ \dfrac{4\sqrt{3}}{3} $ ,
所以圆锥外接球表面积为 $ 4\mathrm{\pi }×{\left(\dfrac{4\sqrt{3}}{3}\right) ^ {2}}=\dfrac{64\mathrm{\pi }}{3} $ .
24.如图,圆锥 $ PO $ 的底面半径和高均是 $ a $ .
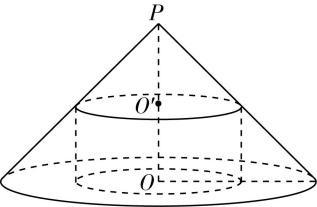
(1) 过线段 $ PO $ 的中点 $ O^\prime $ 作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的体积;
(2) 若过线段 $ PO $ 上的任意一点作平行于底面的截面,并以该截面为底面挖去一个圆柱,求剩下几何体的最大表面积.
答案:(1) 【解】如图,设圆锥母线 $ PB $ 与圆柱的交点为 $ A $ ,连接 $ O^\prime A $ .

又 $ O^\prime $ 为 $ PO $ 的中点,设圆柱的高为 $ h $ ,则 $ h=\dfrac{1}{2}PO=\dfrac{1}{2}a $ .
设圆柱底面的半径为 $ r $ ,则 $ r=O^\prime A=\dfrac{1}{2}OB=\dfrac{1}{2}a. $
因为圆锥内部挖去一个圆柱,故剩下几何体的体积 $ V=\dfrac{1}{3}\mathrm{\pi }{a}^{2}×a-\mathrm{\pi }×{\left(\dfrac{1}{2}a\right) ^ {2}}×\dfrac{1}{2}a=\dfrac{5}{24}\mathrm{\pi }{a}^{3} $ .
(2) 设圆柱的半径为 $ r $ , $ 0 < r < a $ ,高为 $ h $ ,
则依题意,有 $ \dfrac{PO-h}{PO}=\dfrac{r}{a} $ ,即 $ \dfrac{a-h}{a}=\dfrac{r}{a} $ ,所以 $ h=a-r $ .
依题意, $ \mathrm{\angle }POB=\dfrac{\mathrm{\pi }}{2} $ ,则有 $ PB=\sqrt{{a}^{2}+{a}^{2}}=\sqrt{2}a $ .
又圆锥内部挖去一个圆柱,所以剩下几何体的表面积 $ S=\mathrm{\pi }{a}^{2}+\mathrm{\pi }a×\sqrt{2}a+2\mathrm{\pi }×r×h=\mathrm{\pi }{a}^{2}+\mathrm{\pi }a×\sqrt{2}a+2\mathrm{\pi }×r×(a-r)=-2\mathrm{\pi }×{\left(r-\dfrac{a}{2}\right) ^ {2}}+\dfrac{3\mathrm{\pi }}{2}{a}^{2}+\sqrt{2}\mathrm{\pi }{a}^{2} $ ,
所以当 $ r=\dfrac{a}{2} $ 时, $ S $ 取到最大值 $ \dfrac{3+2\sqrt{2}}{2}\mathrm{\pi }{a}^{2} $ .
解析:

 (多选)
(多选)




 (多选)
(多选)













