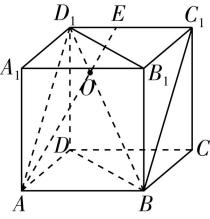
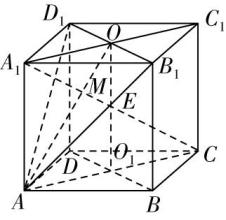
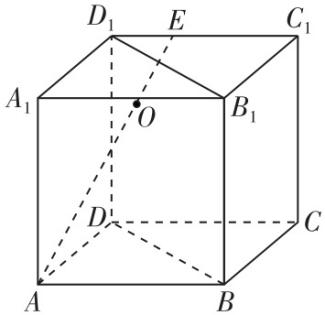
3.如图,在正方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中, $ E $ 为棱 $ {D}_{1}{C}_{1} $ 上靠近点 $ {D}_{1} $ 的三等分点.设 $ AE $ 与平面 $ B{B}_{1}{D}_{1}D $ 的交点为 $ O $ ,则( )
A.三点 $ {D}_{1} $ , $ O $ , $ B $ 共线,且 $ OB=2O{D}_{1} $
B.三点 $ {D}_{1} $ , $ O $ , $ B $ 共线,且 $ OB=3O{D}_{1} $
C.三点 $ {D}_{1} $ , $ O $ , $ B $ 不共线,且 $ OB=2O{D}_{1} $
D.三点 $ {D}_{1} $ , $ O $ , $ B $ 不共线,且 $ OB=3O{D}_{1} $
如图,连接 $ A{D}_{1} $ , $ B{C}_{1} $ , $ B{D}_{1} $ ,
$ \because O\in $ 直线 $ AE $ , $ AE\subset $ 平面 $ AB{C}_{1}{D}_{1} $ ,
$ \therefore O\in $ 平面 $ AB{C}_{1}{D}_{1} $ .
又 $ \because O\in $ 平面 $ B{B}_{1}{D}_{1}D $ ,平面 $ AB{C}_{1}{D}_{1}\cap $ 平面 $ B{B}_{1}{D}_{1}D=B{D}_{1} $ , $ \therefore O\in $ 直线 $ B{D}_{1} $ , $ \therefore {D}_{1} $ , $ O $ , $ B $ 三点共线.
$ \because AB//{C}_{1}{D}_{1} $ , $ \therefore △ABO\sim △E{D}_{1}O $ , $ \therefore OB:O{D}_{1}=AB:E{D}_{1}=3:1 $ , $ \therefore OB=3O{D}_{1} $ .
故选 $ \mathrm{B} $ .