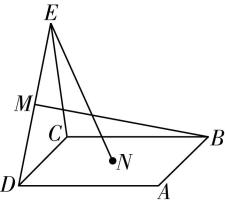
1.如图,点 $ N $ 为正方形 $ ABCD $ 的中心,点 $ E $ 在平面 $ ABCD $ 外, $ M $ 是线段 $ ED $ 的中点,则下列各选项中两条直线不是异面直线的为( )
A. $ AB $ 与 $ DE $
B. $ BC $ 与 $ EN $
C. $ CD $ 与 $ BM $
D. $ BM $ 与 $ EN $
在正方形 $ ABCD $ 中, $ AB//CD $ ,所以 $ D $ 在平面 $ ABCD $ 内, $ D $ 不在直线 $ AB $ 上,又 $ E $ 不在平面 $ ABCD $ 内,所以 $ AB $ 与 $ DE $ 异面;
因为 $ BC\subset $ 平面 $ ABCD $ , $ N $ 在平面 $ ABCD $ 内, $ N $ 不在直线 $ BC $ 上,又 $ E $ 不在平面 $ ABCD $ 内,所以 $ BC $ 与 $ EN $ 异面;
因为 $ CD\subset $ 平面 $ ABCD $ , $ B $ 在平面 $ ABCD $ 内, $ B $ 不在直线 $ CD $ 上,又 $ M $ 不在平面 $ ABCD $ 内,所以 $ CD $ 与 $ BM $ 异面;
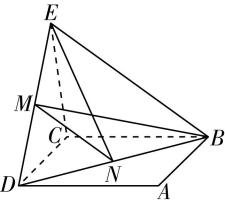
连接 $ BD $ , $ BE $ , $ MN $ ,因为点 $ N $ 为正方形 $ ABCD $ 的中心,又 $ M $ 是线段 $ ED $ 的中点,
所以 $ MN//BE $ ,所以 $ B $ , $ M $ , $ N $ , $ E $ 在平面 $ BDE $ 内,所以 $ BM $ 与 $ EN $ 不是异面直线.
故选 $ \mathrm{D} $ .
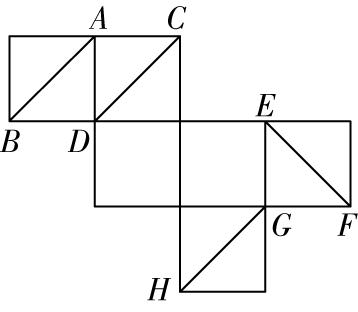 (多选)
(多选)