第8.4节综合训练

平面五边形的五个顶点中任意三点和四点均不共线，但这五点共面，故 $ \mathrm{A} $ ， $ \mathrm{B} $ 错误；

若空间五点中有三点共线，则这五点不一定共面，故 $ \mathrm{C} $ 错误；

若空间五点中有四点共线，则由推论1可知，直线与直线外一点可确定唯一一个平面，即这五点一定共面，故 $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .

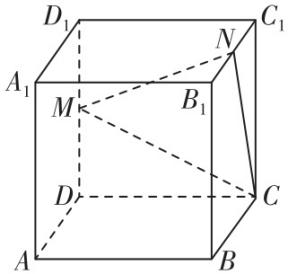
如图,在正方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中,

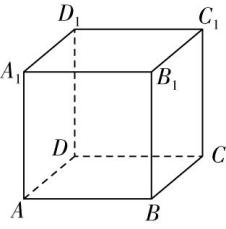
若 $ \alpha $ 是平面 $ ABCD $ , $ {A}_{1}{B}_{1} $ 为 $ m $ , $ AB $ 为 $ n $ ,此时 $ m $ 与 $ n $ 平行,故 $ \mathrm{A} $ 正确；

若 $ \alpha $ 是平面 $ ABCD $ , $ {A}_{1}{D}_{1} $ 为 $ m $ , $ AB $ 为 $ n $ ,此时 $ m\perp n $ ,且 $ m $ 与 $ n $ 异面,故 $ \mathrm{B} $ , $ \mathrm{D} $ 正确；

若 $ m//\alpha $ ,则 $ m $ 与平面 $ \alpha $ 无交点,又 $ n\subset \alpha $ ,则 $ m $ 与 $ n $ 无交点,即 $ m $ 与 $ n $ 不可能相交,故 $ \mathrm{C} $ 错误.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .

对于 $ \mathrm{A} $ , $ \because CD\subset $ 平面 $ BCD $ , $ B\in $ 平面 $ BCD $ , $ B\notin CD $ , $ A\notin $ 平面 $ BCD $ ,由异面直线的定义可知,直线 $ AB $ 与 $ CD $ 是异面直线,故 $ \mathrm{A} $ 正确；

对于 $ \mathrm{B} $ ,如图①, $ \because C $ , $ D $ 分别为所在棱的中点, $ \therefore CD//EF $ ,又 $ AB//EF $ , $ \therefore $ 由平行的传递性可得 $ AB//CD $ ,故 $ \mathrm{B} $ 错误；

图①

对于 $ \mathrm{C} $ ,如图②,取 $ HG $ 的中点 $ F $ ,连接 $ DF $ , $ AF $ ,则 $ DF//GE $ 且 $ DF=\dfrac{1}{2}GE $ ,又 $ AC//GE $ 且 $ AC=\dfrac{1}{2}GE $ , $ \therefore DF//AC $ 且 $ DF=AC $ , $ \therefore A $ , $ C $ , $ D $ 三点确定平面 $ ACDF $ , $ \because B\notin $ 平面 $ ACDF $ , $ A\notin CD $ , $ \therefore AB $ 与 $ CD $ 异面,故 $ \mathrm{C} $ 正确；

图②

对于 $ \mathrm{D} $ , $ \because AB\subset $ 平面 $ ABC $ , $ C\in $ 平面 $ ABC $ , $ C\notin AB $ , $ D\notin $ 平面 $ ABC $ , $ \therefore $ 由异面直线的定义可知,直线 $ AB $ 与 $ CD $ 是异面直线,故 $ \mathrm{D} $ 正确．故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ ．

在平面 $ CD{D}_{1}{C}_{1} $ 中，延长 $ CM $ 交 $ {C}_{1}{D}_{1} $ 的延长线于点 $ P $ ，由点 $ P\in CM $ ,得 $ P\in $ 平面 $ MNC $ ,所以平面 $ MNC $ 即平面 $ PNC $ ,连接 $ PN $ ，则 $ PN $ 与 $ {A}_{1}{D}_{1} $ 的交点即直线 $ {A}_{1}{D}_{1} $ 与平面 $ MNC $ 的交点 $ Q $ .

在 $ △PC{C}_{1} $ 中， $ {D}_{1}M//C{C}_{1} $ , $ {D}_{1}M=\dfrac{1}{2}C{C}_{1} $ ,则 $ {D}_{1}P={C}_{1}{D}_{1} $ ,又在 $ △P{C}_{1}N $ 中， $ {D}_{1}Q//N{C}_{1} $ , $ {D}_{1}P={C}_{1}{D}_{1} $ ,则 $ {D}_{1}Q=\dfrac{1}{2}N{C}_{1}=\dfrac{1}{4}{B}_{1}{C}_{1}=1 $ .故选 $ \mathrm{C} $ .

对于①,连接 $ AC $ , $ PM $ , $ {A}_{1}{C}_{1} $ ,如图①所示,

图①

由 $ M $ , $ P $ 分别是 $ {C}_{1}{D}_{1} $ , $ {A}_{1}{D}_{1} $ 的中点,可得 $ PM//{A}_{1}{C}_{1}//AC $ ,可得 $ AP $ 与 $ CM $ 共面,故①错误；

对于②,因为 $ AP\subset $ 平面 $ ACMP $ , $ M\in $ 平面 $ ACMP $ , $ M\notin AP $ , $ \mathbf{N}\notin $ 平面 $ ACMP $ ,所以由异面直线的定义可得, $ AP $ 与 $ MN $ 是异面直线,则 $ AP $ , $ MN $ , $ D{D}_{1} $ 不会相交于一点,故②错误；

对于③,由①知,过 $ A $ , $ M $ , $ P $ 的平面截正方体所得的图形为四边形 $ ACMP $ ,而 $ PM//AC $ , $ PM=\dfrac{1}{2}AC $ ,故四边形 $ ACMP $ 不是平行四边形,是梯形,故③错误；

对于④,如图②,连接 $ AN $ 并延长交 $ DC $ 的延长线于点 $ E $ ,则 $ CE=CD $ ,连接 $ EM $ 并延长交 $ D{D}_{1} $ 的延长线于点 $ F $ ,交 $ C{C}_{1} $ 于点 $ H $ ,连接 $ NH $ ,则 $ CH=\dfrac{2}{3}C{C}_{1}=\dfrac{2}{3}D{D}_{1} $ , $ {D}_{1}F=\dfrac{1}{3}D{D}_{1} $ ,连接 $ AF $ 交 $ {A}_{1}{D}_{1} $ 于点 $ G $ ,连接 $ GM $ ,则 $ G{D}_{1}=\dfrac{1}{4}AD=\dfrac{1}{4}{A}_{1}{D}_{1} $ ,此时所得的五边形 $ ANHMG $ 即过点 $ A $ , $ M $ , $ N $ 的平面截正方体所得的图形,故④正确.

图②

故选 $ \mathrm{C} $ .