1.(多选)下列说法中,正确的结论有( )(多选)
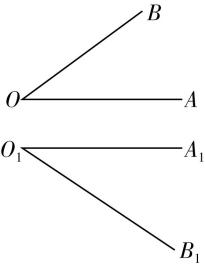
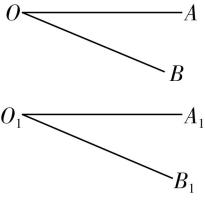
A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等
B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等
C.如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行
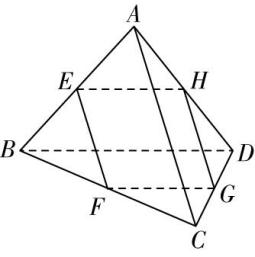
对于选项 $ \mathrm{A} $ ,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,故 $ \mathrm{A} $ 错误;对于选项 $ \mathrm{B} $ ,如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等,故 $ \mathrm{B} $ 正确;对于选项 $ \mathrm{C} $ ,如果一个角的两边和另一个角的两边分别垂直,这两个角的大小关系不确定,既可能相等也可能互补,也可能既不相等,也不互补,如图,在正方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中, $ \mathrm{\angle }{A}_{1}{D}_{1}{C}_{1} $ 与 $ \mathrm{\angle }{A}_{1}B{C}_{1} $ 满足 $ {A}_{1}{D}_{1}\perp {A}_{1}B $ , $ {C}_{1}{D}_{1}\perp {C}_{1}B $ ,但是 $ \mathrm{\angle }{A}_{1}{D}_{1}{C}_{1}=\dfrac{\mathrm{\pi }}{2} $ , $ \mathrm{\angle }{A}_{1}B{C}_{1}=\dfrac{\mathrm{\pi }}{3} $ ,二者既不相等也不互补,故 $ \mathrm{C} $ 错误;
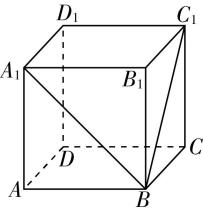
对于选项 $ \mathrm{D} $ ,如果两条直线同时平行于第三条直线,那么这两条直线平行,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .