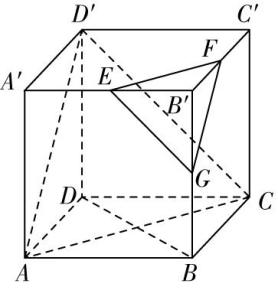
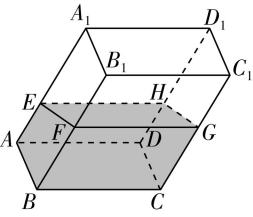
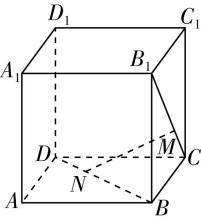
5.如图所示,正方体 $ ABCD-A^\prime B^\prime C^\prime D^\prime $ 的棱长为 $ {\rm 2,} E $ , $ F $ 分别为 $ A^\prime B^\prime $ , $ B^\prime C^\prime $ 的中点,点 $ G $ 满足 $ \overrightarrow {B^\prime G}=\lambda \overrightarrow {B^\prime B} $ .
(2) 连接 $ BD $ ,点 $ M $ 在线段 $ BD $ 上,且满足 $ D^\prime M// $ 平面 $ EFG $ ,当 $ \lambda \in [\dfrac{1}{2},1] $ 时,求 $ D^\prime M $ 长度的取值范围.
答案:(1) 【证明】连接 $ A^\prime B $ ,如图①所示.
当 $ \lambda =\dfrac{1}{2} $ 时, $ \overrightarrow {B^\prime G}=\dfrac{1}{2}\overrightarrow {B^\prime B} $ ,所以 $ G $ 为 $ BB\prime $ 的中点,又因为 $ E $ 为 $ A^\prime B^\prime $ 的中点,所以 $ EG//A^\prime B $ .
因为 $ A^\prime D^\prime //BC $ 且 $ A^\prime D^\prime =BC $ ,所以四边形 $ A^\prime D^\prime CB $ 为平行四边形,所以 $ A^\prime B//D^\prime C $ ,故 $ EG//D^\prime C $ .
又 $ EG\not\subset $ 平面 $ D^\prime AC $ , $ D^\prime C\subset $ 平面 $ D^\prime AC $ ,
所以 $ EG// $ 平面 $ D^\prime AC $ .

图①
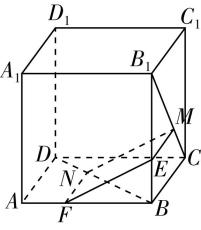
(2) 【解】连接 $ B^\prime D^\prime $ 交 $ EF $ 于点 $ H $ ,连接 $ HG $ ,连接 $ A^\prime C^\prime $ ,交 $ B^\prime D^\prime $ 于点 $ {O}_{1} $ .
当 $ \lambda =\dfrac{1}{2} $ 时, $ G $ 为 $ BB\prime $ 的中点,取 $ BD $ 与 $ AC $ 的交点为 $ {O}_{2} $ ,连接 $ B{O}_{1} $ , $ D^\prime {O}_{2} $ ,如图②所示,

图②
因为 $ E $ , $ F $ 分别为 $ A^\prime B^\prime $ , $ B^\prime C^\prime $ 的中点,所以 $ EF//A^\prime C^\prime $ ,
则 $ H $ 为 $ B^\prime {O}_{1} $ 的中点,又 $ G $ 为 $ BB\prime $ 的中点,所以 $ HG//B{O}_{1} $ .
又 $ B{O}_{2}//D^\prime {O}_{1} $ 且 $ B{O}_{2}=D^\prime {O}_{1} $ ,
所以四边形 $ B{O}_{2}D^\prime {O}_{1} $ 为平行四边形,
所以 $ B{O}_{1}//D^\prime {O}_{2} $ ,故 $ GH//D^\prime {O}_{2} $ .
又 $ D^\prime M// $ 平面 $ EFG $ ,平面 $ D^\prime DBB\prime \cap $ 平面 $ EFG=GH $ , $ D^\prime M\subset $ 平面 $ D^\prime DBB\prime $ ,
所以 $ D^\prime M//GH $ ,即 $ M $ 和 $ {O}_{2} $ 重合.
又 $ BD=\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2} $ ,此时 $ D^\prime M=\sqrt{{2}^{2}+{\left(\sqrt{2}\right) ^ {2}}}=\sqrt{6} $ .
当 $ \lambda =1 $ 时,点 $ G $ 与点 $ B $ 重合,在 $ DB $ 上取点 $ M $ 使得 $ \overrightarrow {DM}=\dfrac{1}{4}\overrightarrow {DB} $ ,连接 $ D^\prime M $ ,如图③所示,

图③
由前述可知 $ H $ 为 $ B^\prime {O}_{1} $ 的中点,则 $ D^\prime H=\dfrac{3}{4}D^\prime B^\prime $ .又 $ BM=\dfrac{3}{4}DB $ ,所以 $ D^\prime H=BM $ ,又 $ D^\prime B^\prime //BD $ ,所以四边形 $ D^\prime HBM $ 为平行四边形,
所以 $ D^\prime M//HB $ .
又 $ HB\subset $ 平面 $ EFG $ , $ D^\prime M\not\subset $ 平面 $ EFG $ ,所以 $ D^\prime M// $ 平面 $ EFG $ ,
所以 $ D^\prime M=\sqrt{{2}^{2}+{\left(\dfrac{\sqrt{2}}{2}\right) ^ {2}}}=\dfrac{3\sqrt{2}}{2} $ .
综上可得,当 $ \lambda $ 从 $ \dfrac{1}{2} $ 增大至1时,点 $ M $ 从 $ BD $ 的中点逐渐移动到 $ BD $ 上靠近点 $ D $ 的四等分点处,则当 $ \lambda \in [\dfrac{1}{2},1] $ 时, $ D^\prime M $ 长度的取值范围为 $ [\dfrac{3\sqrt{2}}{2},\sqrt{6}] $ .






 (多选)
(多选)