1.平面 $ \alpha $ 与平面 $ \beta $ 平行的充分条件可以是( )
A.平面 $ \alpha $ 内的任意一条直线都与平面 $ \beta $ 平行
B.直线 $ n// $ 平面 $ \alpha $ ,直线 $ n// $ 平面 $ \beta $ ,且直线 $ n $ 不在平面 $ \alpha $ 内,也不在平面 $ \beta $ 内
C.直线 $ a\subset $ 平面 $ \alpha $ ,直线 $ b\subset $ 平面 $ \beta $ ,且 $ a// $ 平面 $ \beta $ ,直线 $ b// $ 平面 $ \alpha $
D.平面 $ \alpha $ 内有无穷多条直线都与平面 $ \beta $ 平行
对于选项 $ \mathrm{A} $ :由任意一条直线都与平面 $ \beta $ 平行,一定能找到两条相交的直线 $ a $ , $ b $ 使得直线 $ a// $ 平面 $ \beta $ ,直线 $ b// $ 平面 $ \beta $ ,又两条相交直线在平面 $ \alpha $ 内,由面面平行的判定定理即可得到 $ \alpha //\beta $ ,故 $ \mathrm{A} $ 正确;
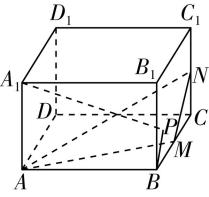
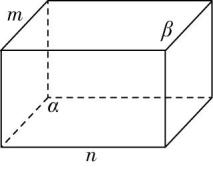
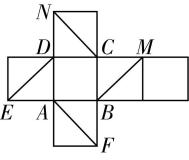
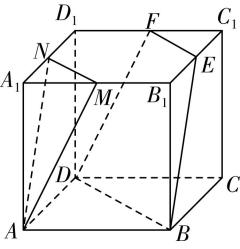
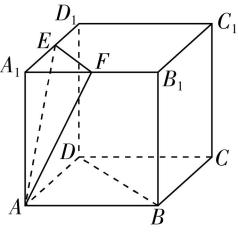
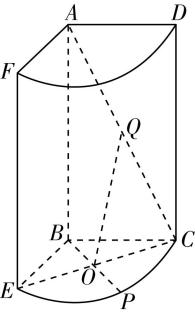
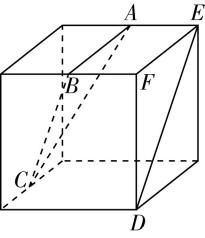
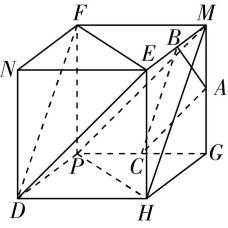
对于选项 $ \mathrm{B} $ :由图①可知直线 $ n// $ 平面 $ \alpha $ ,直线 $ n// $ 平面 $ \beta $ ,且直线 $ n $ 不在平面 $ \alpha $ 内,也不在平面 $ \beta $ 内,但平面 $ \alpha $ 与平面 $ \beta $ 相交,故 $ \mathrm{B} $ 错误;
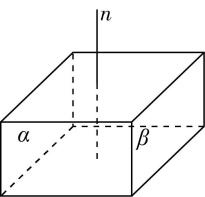
图①
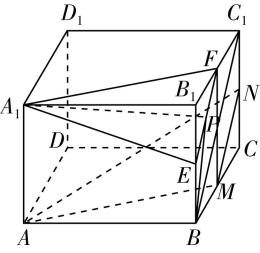
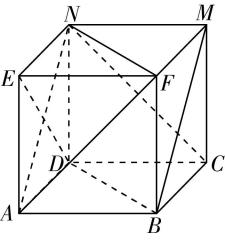
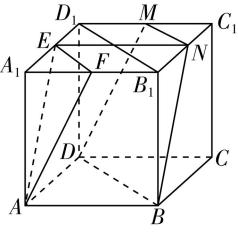
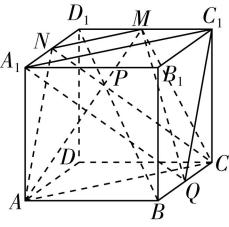
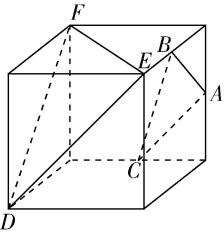
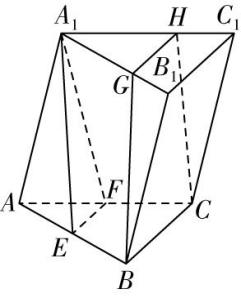
对于选项 $ \mathrm{C} $ :由图②可知,直线 $ a\subset $ 平面 $ \alpha $ ,直线 $ b\subset $ 平面 $ \beta $ ,且直线 $ a// $ 平面 $ \beta $ ,直线 $ b// $ 平面 $ \alpha $ ,但平面 $ \alpha $ 与平面 $ \beta $ 相交,故 $ \mathrm{C} $ 错误;
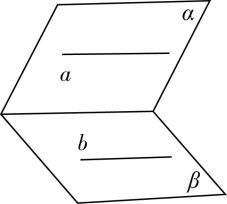
图②
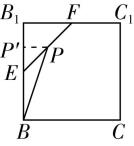
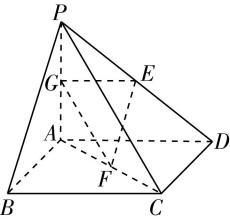
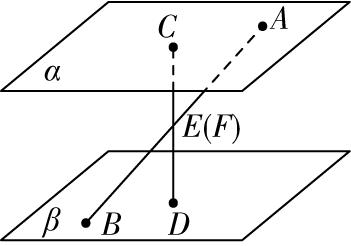
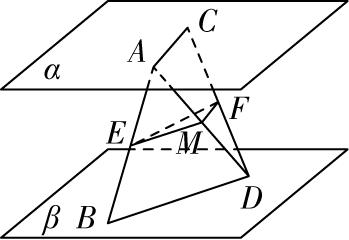
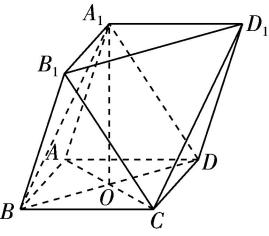
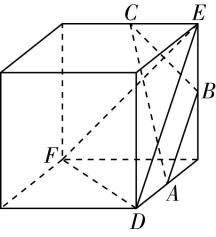
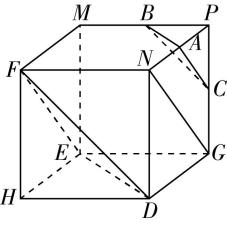
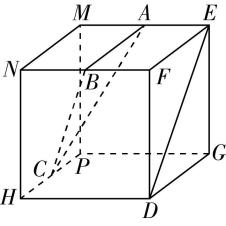
对于选项 $ \mathrm{D} $ :由图③可知,直线 $ a\subset $ 平面 $ \alpha $ ,且 $ a//\beta $ ,则平面 $ \alpha $ 内只要与直线 $ a $ 平行且不与平面 $ \alpha $ 和平面 $ \beta $ 的交线重合的直线都与平面 $ \beta $ 平行,这样的直线有无数条,但是平面 $ \alpha $ 与平面 $ \beta $ 相交,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A} $ .
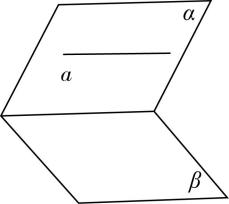
图③

 (多选)
(多选)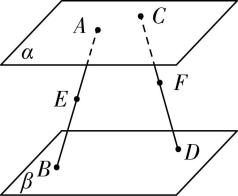




 (多选)
(多选)