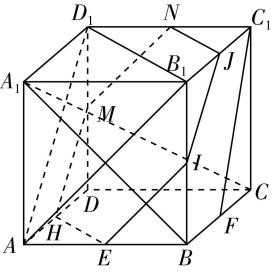
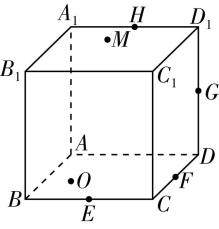
6.在长方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中, $ AB=2 $ , $ AD=1 $ , $ A{A}_{1}=1 $ , $ E $ , $ F $ , $ G $ , $ H $ 分别为 $ BC $ , $ CD $ , $ D{D}_{1} $ , $ {D}_{1}{A}_{1} $ 的中点.
(2) 点 $ M $ 在矩形 $ {A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 内(不含边界)运动,若 $ M\in $ 平面 $ EFH $ ,求点 $ M $ 运动轨迹的长度;
(3) 点 $ O $ 在矩形 $ ABCD $ 内(不含边界)运动,若直线 $ {A}_{1}O// $ 平面 $ EFH $ ,求 $ {A}_{1}O+OC $ 的最小值.
答案:(1) 【证明】如图①,连接 $ FG $ , $ C{D}_{1} $ ,

图①
因为 $ F $ , $ G $ 分别为 $ CD $ , $ D{D}_{1} $ 的中点,
所以 $ FG//C{D}_{1} $ .
在长方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中, $ H $ , $ E $ 分别为 $ {A}_{1}{D}_{1} $ , $ BC $ 的中点,所以 $ H{D}_{1}//EC $ 且 $ H{D}_{1}=EC $ ,
所以四边形 $ EC{D}_{1}H $ 是平行四边形,所以 $ C{D}_{1}//EH $ ,所以 $ FG//EH $ ,
所以 $ E $ , $ F $ , $ G $ , $ H $ 四点共面,即 $ G\in $ 平面 $ EFH $ .
(2) 【解】如图①,取线段 $ {A}_{1}{B}_{1} $ 的中点 $ T $ ,连接 $ TH $ , $ {B}_{1}{D}_{1} $ , $ BD $ .
在 $ △{A}_{1}{B}_{1}{D}_{1} $ 中, $ T $ , $ H $ 分别是 $ {A}_{1}{B}_{1} $ , $ {A}_{1}{D}_{1} $ 的中点,
所以 $ TH//{B}_{1}{D}_{1} $ ,同理可证 $ EF//BD $ ,
在长方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中,因为 $ {B}_{1}{D}_{1}//BD $ ,所以 $ TH//EF $ ,即 $ E $ , $ F $ , $ H $ , $ T $ 四点共面.
所以点 $ M $ 的轨迹是线段 $ TH $ (不含两个端点),
由 $ TH=\sqrt{1+\dfrac{1}{4}}=\dfrac{\sqrt{5}}{2} $ ,得点 $ M $ 运动轨迹的长度为 $ \dfrac{\sqrt{5}}{2} $ .
(3) 【解】连接 $ {A}_{1}B $ , $ {A}_{1}D $ ,如图①,
由 $ E $ , $ F $ 分别为 $ BC $ , $ CD $ 的中点,得 $ BD//EF $ ,
因为 $ BD\not\subset $ 平面 $ EFH $ , $ EF\subset $ 平面 $ EFH $ ,所以 $ BD// $ 平面 $ EFH $ .
在长方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中, $ {A}_{1}H//BE $ , $ {A}_{1}H=BE $ ,
所以四边形 $ {A}_{1}BEH $ 是平行四边形,所以 $ {A}_{1}B//HE $ ,
因为 $ {A}_{1}B\not\subset $ 平面 $ EFH $ , $ HE\subset $ 平面 $ EFH $ ,所以 $ {A}_{1}B// $ 平面 $ EFH $ ,
因为 $ {A}_{1}B $ , $ BD\subset $ 平面 $ {A}_{1}BD $ , $ {A}_{1}B\cap BD=B $ ,所以平面 $ {A}_{1}BD// $ 平面 $ EFH $ ,
所以当 $ O\in BD $ 时,由 $ {A}_{1}O\subset $ 平面 $ {A}_{1}BD $ ,得 $ {A}_{1}O// $ 平面 $ EFH $ ,
即点 $ O $ 的轨迹是线段 $ BD $ (不含两个端点).
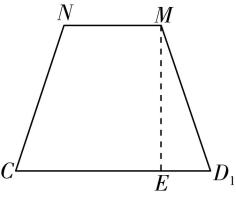
如图②所示,将 $ △{A}_{1}BD $ 沿 $ BD $ 翻折,使 $ △{A}_{1}BD $ 与 $ △BCD $ 在同一平面,

图②
要使 $ {A}_{1}O+OC $ 最小,只需 $ {A}_{1} $ , $ O $ , $ C $ 三点共线,此时最小值为线段 $ {A}_{1}C $ 的长度.
在长方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中,
$ {A}_{1}B=\sqrt{4+1}=\sqrt{5} $ , $ {A}_{1}D=\sqrt{1+1}=\sqrt{2} $ , $ BD=\sqrt{4+1}=\sqrt{5} $ , $ BC=1 $ , $ CD=2 $ ,
设 $ \mathrm{\angle }{A}_{1}BD=\alpha $ , $ \mathrm{\angle }DBC=\beta $ ,
在 $ △{A}_{1}BD $ 中,由余弦定理得 $ \cos \alpha =\dfrac{5+5-2}{2×\sqrt{5}×\sqrt{5}}=\dfrac{4}{5} $ ,
由 $ \alpha \in (0,\mathrm{\pi }) $ 得 $ \sin \alpha =\sqrt{1-\dfrac{16}{25}}=\dfrac{3}{5} $ ,
在 $ \mathrm{R}\mathrm{t}△BCD $ 中, $ \cos \beta =\dfrac{\sqrt{5}}{5} $ , $ \sin \beta =\dfrac{2\sqrt{5}}{5} $ ,
所以 $ \cos (\alpha +\beta )= \cos \alpha \cos \beta - \sin \alpha \sin \beta =\dfrac{4}{5}×\dfrac{\sqrt{5}}{5}-\dfrac{3}{5}×\dfrac{2\sqrt{5}}{5}=-\dfrac{2\sqrt{5}}{25} $ ,
在 $ △{A}_{1}BC $ 中,由余弦定理得 $ {A}_{1}C=\sqrt{5+1-2\sqrt{5}×(-\dfrac{2\sqrt{5}}{25})}=\dfrac{\sqrt{170}}{5} $ ,
所以 $ {A}_{1}O+OC $ 的最小值为 $ \dfrac{\sqrt{170}}{5} $ .
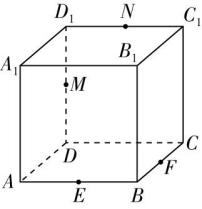 (多选)
(多选)