8.6.1 直线与直线垂直+8.6.2 直线与平面垂直

如图,取棱 $ AP $ 的中点为 $ F $ ,连接 $ EF $ , $ BF $ .

因为 $ E $ 为 $ PC $ 的中点,所以 $ EF//AC $ , $ EF=\dfrac{1}{2}AC $ ,

所以异面直线 $ BE $ 与 $ AC $ 所成角为 $ \mathrm{\angle }BEF $ （或其补角）.

不妨设正四棱锥 $ P-ABCD $ 的所有棱长均为2,

则 $ BE=BF=\sqrt{3} $ , $ EF=\dfrac{1}{2}AC=\sqrt{2} $ ,

所以 $ \cos \mathrm{\angle }BEF=\dfrac{\dfrac{1}{2}EF}{BE}=\dfrac{\dfrac{\sqrt{2}}{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{6} $ .

故选 $ \mathrm{D} $ .

如图,取 $ D{D}_{1} $ 的中点 $ G $ ,连接 $ EG $ , $ FG $ ,

在 $ △BD{D}_{1} $ 中, $ G $ 为 $ D{D}_{1} $ 的中点, $ E $ 为 $ B{D}_{1} $ 的中点,所以 $ EG//BD $ ,

则 $ \mathrm{\angle }GEF $ 为异面直线 $ EF $ 与 $ BD $ 所成的角或其补角.

设正方体的棱长为2,则 $ EG=\dfrac{1}{2}BD=\dfrac{1}{2}\sqrt{A{B}^{2}+A{D}^{2}}=\sqrt{2} $ ,

连接 $ A{C}_{1} $ , $ DF $ , $ B{C}_{1} $ ,易知 $ E $ 为 $ A{C}_{1} $ 的中点,又 $ F $ 为 $ AB $ 的中点,

所以在 $ △AB{C}_{1} $ 中, $ EF=\dfrac{1}{2}B{C}_{1}=\dfrac{1}{2}\sqrt{B{C}^{2}+{C}_{1}{C}^{2}}=\sqrt{2} $ .

又 $ DF=\sqrt{A{D}^{2}+A{F}^{2}}=\sqrt{5} $ , $ GF=\sqrt{D{F}^{2}+D{G}^{2}}=\sqrt{6} $ ,

在 $ △GEF $ 中, $ \cos \mathrm{\angle }GEF=\dfrac{E{G}^{2}+E{F}^{2}-G{F}^{2}}{2EG\cdot EF}=-\dfrac{1}{2} $ ,

所以 $ \mathrm{\angle }GEF={120}^{\circ } $ ,则异面直线 $ EF $ 与 $ BD $ 所成的角为 $ {60}^{\circ } $ .故选 $ \mathrm{C} $ .

充分性：只有当 $ l $ 垂直于 $ \alpha $ 内的两条相交直线时,才可推出 $ l\perp \alpha $ ,由题可知, $ l $ 垂直于 $ \alpha $ 内的一条直线 $ m $ ,则 $ l $ 可能与平面 $ \alpha $ 斜交、平行或在平面 $ \alpha $ 内,无法推出 $ l\perp \alpha $ ,充分性不成立；

必要性：若 $ l\perp \alpha $ ,又 $ m\subset \alpha $ ,则 $ l\perp m $ ,必要性成立.

综上所述,“ $ l\perp m $ ”是“ $ l\perp \alpha $ ”的必要不充分条件.故选 $ \mathrm{B} $ .

对于 $ \mathrm{A} $ ,易证 $ AB $ 与 $ CE $ 所成的角为 $ {45}^{\circ } $ ,所以直线 $ AB $ 与平面 $ CDE $ 不垂直；对于 $ \mathrm{B} $ ,易证 $ AB\perp CE $ , $ AB\perp ED $ ,且 $ CE\cap ED=E $ , $ CE $ , $ ED\subset $ 平面 $ CDE $ ,所以 $ AB\perp $ 平面 $ CDE $ ；对于 $ \mathrm{C} $ ,易证 $ AB $ 与 $ CE $ 所成的角为 $ {60}^{\circ } $ ,所以直线 $ AB $ 与平面 $ CDE $ 不垂直；对于 $ \mathrm{D} $ ,连接 $ AC $ ,易证 $ ED\perp $ 平面 $ ABC $ ,得 $ ED\perp AB $ ,同理证得 $ EC\perp AB $ ,且 $ ED\cap EC=E $ , $ ED $ , $ EC\subset $ 平面 $ CDE $ ,所以 $ AB\perp $ 平面 $ CDE $ .故选 $ \mathrm{B}\mathrm{D} $ .

对于 $ \mathrm{A} $ ,因为在正方形 $ S{G}_{1}{G}_{2}{G}_{3} $ 中, $ S{G}_{1}\perp {G}_{1}E $ , $ S{G}_{3}\perp {G}_{3}F $ ,所以在四面体 $ S-EFG $ 中, $ SG\perp GE $ , $ SG\perp GF $ ,因为 $ GE\cap GF=G $ , $ GE $ , $ GF\subset $ 平面 $ EFG $ ,所以 $ SG\perp $ 平面 $ EFG $ ,所以 $ \mathrm{A} $ 正确.

对于 $ \mathrm{B} $ ,因为 $ SG\perp $ 平面 $ EFG $ , $ GD\subset $ 平面 $ EFG $ ,所以 $ SG\perp GD $ ,所以 $ \mathrm{\angle }SGD={90}^{\circ } $ ,所以 $ \mathrm{\angle }SDG $ 不可能为直角,所以 $ SD $ 与 $ GD $ 不垂直,所以 $ SD $ 与平面 $ EFG $ 不可能垂直,所以 $ \mathrm{B} $ 错误.

对于 $ \mathrm{C} $ ,由题意可知 $ △GEF $ 为等腰直角三角形,且 $ GE=GF $ , $ \mathrm{\angle }GFE={45}^{\circ } $ ,所以 $ GF $ 与平面 $ SEF $ 不可能垂直,所以 $ \mathrm{C} $ 错误.

对于 $ \mathrm{D} $ ,由选项 $ \mathrm{B} $ 的解析可知, $ \mathrm{\angle }SDG $ 不可能为直角,所以 $ SD $ 与 $ GD $ 不垂直,所以 $ GD $ 与平面 $ SEF $ 不可能垂直,所以 $ \mathrm{D} $ 错误.故选 $ \mathrm{A} $ ．

$ \mathrm{A} $ 选项,若 $ m//\alpha $ , $ n//\alpha $ ,则 $ m $ 与 $ n $ 可能相交、异面或平行, $ \mathrm{A} $ 错误；

$ \mathrm{B} $ 选项,若 $ m//n $ , $ n\subset \alpha $ ,则 $ m//\alpha $ 或 $ m\subset \alpha $ , $ \mathrm{B} $ 错误；

$ \mathrm{C} $ 选项, $ m//\alpha $ ,则存在过直线 $ m $ 的平面 $ \beta $ ,使得 $ \beta \cap \alpha =c $ ,则 $ m//c $ ,而 $ n\perp \alpha $ , $ c\subset \alpha $ ,则 $ n\perp c $ ,故 $ m\perp n $ , $ \mathrm{C} $ 正确；

$ \mathrm{D} $ 选项,若 $ m\perp \alpha $ , $ n\perp m $ ,则 $ n//\alpha $ 或 $ n\subset \alpha $ , $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .

对于A，因为平行于同一直线的两个平面可能平行，也可能相交，所以A不正确．

对于B，设 $ \alpha //\beta $ ， $ \beta //\gamma $ ，取直线 $ a $ , $ b\subset \alpha $ ，且 $ a\cap b=A $ ，因为 $ \alpha //\beta $ ，所以在 $ \beta $ 内存在 $ {a}_{1}//a $ ， $ {b}_{1}//b $ ，且 $ {a}_{1}\cap {b}_{1}={A}_{1} $ ．又因为 $ \beta //\gamma $ ，所以在 $ \gamma $ 内存在 $ {a}_{2}//{a}_{1} $ ， $ {b}_{2}//{b}_{1} $ ，且 $ {a}_{2}\cap {b}_{2}={A}_{2} $ ，

因此 $ a//{a}_{2} $ ， $ b//{b}_{2} $ ．又因为 $ a\not\subset \gamma $ ， $ {a}_{2}\subset \gamma $ ，所以 $ a//\gamma $ ，同理可得 $ b//\gamma $ ，而 $ a\cap b=A $ ， $ a $ , $ b\subset \alpha $ ，因此 $ \alpha //\gamma $ ，所以B正确．

对于C，因为垂直于同一直线的两直线可能平行、相交或异面，所以C不正确．

对于D，由线面垂直的性质知垂直于同一平面的两直线平行，所以D正确．

故选 $ \mathrm{B}\mathrm{D} $ ．

如图,连接 $ AO $ 并延长,交 $ BC $ 于点 $ D $ ,连接 $ BO $ 并延长,交 $ AC $ 于点 $ E $ .

因为 $ PA\perp PB $ , $ PA\perp PC $ ,又 $ PB\cap PC=P $ , $ PB $ , $ PC\subset $ 平面 $ PBC $ ,

所以 $ PA\perp $ 平面 $ PBC $ .

因为 $ BC\subset $ 平面 $ PBC $ ,所以 $ PA\perp BC $ .

因为 $ PO\perp $ 平面 $ ABC $ , $ BC\subset $ 平面 $ ABC $ ,所以 $ PO\perp BC $ .

又 $ PA\cap PO=P $ , $ PA $ , $ PO\subset $ 平面 $ PAO $ ,所以 $ BC\perp $ 平面 $ PAO $ .

又 $ AO\subset $ 平面 $ PAO $ ,所以 $ AO\perp BC $ ,即 $ AD\perp BC $ ,

同理可证 $ BE\perp AC $ ,所以 $ O $ 是 $ △ABC $ 的垂心.故选 $ \mathrm{D} $ .

因为 $ DE\perp $ 平面 $ ABC $ , $ PA\perp $ 平面 $ ABC $ ,所以 $ DE//PA $ .又 $ DE\not\subset $ 平面 $ PAC $ , $ PA\subset $ 平面 $ PAC $ ,所以 $ DE// $ 平面 $ PAC $ .

点到平面的距离是指空间内一点到平面内一点的最小长度；直线与平面平行时,直线上任意一点到这个平面的距离,即为这条直线到这个平面的距离,它们都相等；两平行平面间的距离指的是其中一个平面内一点到另外一个平面的距离,两个平行平面的公垂线段都相等,其长度等于两个平行平面间的距离,所以 $ \mathrm{A} $ ， $ \mathrm{B} $ ， $ \mathrm{D} $ 都正确.两条平行直线分别在两个平行平面内，则两条平行直线间的距离不一定是两个平行平面的公垂线段的长度,所以 $ \mathrm{C} $ 错误.故选 $ \mathrm{C} $ .

连接 $ AC $ ,由题意可知, $ AB\perp $ 平面 $ BC{C}_{1}{B}_{1} $ ,又 $ BM\subset $ 平面 $ BC{C}_{1}{B}_{1} $ ,所以 $ AB\perp BM $ , $ BM=\sqrt{B{C}^{2}+C{M}^{2}}=\sqrt{5} $ .

设点 $ C $ 到平面 $ ABM $ 的距离为 $ h $ ,由 $ {V}_{M-ABC}={V}_{C-ABM} $ ,

即 $ \dfrac{1}{3}×\dfrac{1}{2}×2×2×1=\dfrac{1}{3}×\dfrac{1}{2}×2×\sqrt{5}h $ ,解得 $ h=\dfrac{2\sqrt{5}}{5} $ .故选 $ \mathrm{D} $ .

如图,延长 $ MN $ 交 $ DC $ 的延长线于点 $ Q $ ,连接 $ {A}_{1}Q $ , $ {C}_{1}Q $ , $ AC $ .

因为 $ M $ , $ N $ 分别是 $ AB $ , $ BC $ 的中点,所以 $ MN//AC $ .

由正方体的性质可得 $ AC//{A}_{1}{C}_{1} $ ,所以 $ MN//{A}_{1}{C}_{1} $ ,

又 $ {A}_{1}{C}_{1}\subset $ 平面 $ {A}_{1}{C}_{1}D $ , $ MN\not\subset $ 平面 $ {A}_{1}{C}_{1}D $ ,所以 $ MN// $ 平面 $ {A}_{1}{C}_{1}D $ ,

所以 $ MN $ 到平面 $ {A}_{1}{C}_{1}D $ 的距离即点 $ Q $ 到平面 $ {A}_{1}{C}_{1}D $ 的距离,设为 $ h $ .

因为正方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 的棱长为1,

所以 $ DQ=\dfrac{3}{2} $ , $ {A}_{1}D=D{C}_{1}={A}_{1}{C}_{1}=\sqrt{2} $ ,

又 $ {V}_{Q-{A}_{1}{C}_{1}D}={V}_{{A}_{1}-DQ{C}_{1}} $ ,

所以 $ \dfrac{1}{3}{S}_{△{A}_{1}{C}_{1}D}\cdot h=\dfrac{1}{3}{S}_{△DQ{C}_{1}}\cdot {A}_{1}{D}_{1} $ ,即 $ \dfrac{1}{3}×\dfrac{\sqrt{3}}{4}×(\sqrt{2})^{2}×h=\dfrac{1}{3}×\dfrac{1}{2}×\dfrac{3}{2}×1×1⇒h=\dfrac{\sqrt{3}}{2} $ .故选 $ \mathrm{C} $ .

如图,不妨记正方体为 $ {A}_{2}{B}_{2}{C}_{2}{D}_{2}-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ ,连接 $ {A}_{1}{B}_{2} $ , $ {D}_{1}{C}_{2} $ ,易知 $ {A}_{1}{D}_{1}//{B}_{2}{C}_{2} $ , $ {A}_{1}{D}_{1}={B}_{2}{C}_{2} $ ,所以四边形 $ {A}_{1}{D}_{1}{C}_{2}{B}_{2} $ 是平行四边形,所以 $ {A}_{1}{B}_{2}//{C}_{2}{D}_{1} $ .

由题图可知 $ A $ , $ B $ , $ C $ , $ D $ , $ E $ , $ F $ , $ G $ , $ H $ , $ M $ , $ N $ , $ P $ , $ Q $ 均为正方体各棱的中点.

因为 $ E $ , $ Q $ 分别为 $ {A}_{1}{A}_{2} $ , $ {A}_{2}{B}_{2} $ 的中点,

所以 $ EQ//{A}_{1}{B}_{2} $ ,同理可得 $ BG//{C}_{2}{D}_{1} $ ,

又 $ {A}_{1}{B}_{2}//{C}_{2}{D}_{1} $ ,所以 $ EQ//BG $ .又 $ EQ\not\subset $ 平面 $ BCG $ , $ BG\subset $ 平面 $ BCG $ ,所以 $ EQ// $ 平面 $ BCG $ ,同理可得 $ EM// $ 平面 $ BCG $ ,

又 $ EM\cap EQ=E $ , $ EM $ , $ EQ\subset $ 平面 $ EMQ $ ,

所以平面 $ EMQ// $ 平面 $ BCG $ .

连接体对角线 $ {A}_{2}{C}_{1} $ ，分别交平面 $ EMQ $ 和平面 $ BCG $ 于点 $ {M}_{1} $ , $ {N}_{1} $ .

因为 $ {C}_{1}{C}_{2}\perp $ 平面 $ {A}_{2}{B}_{2}{C}_{2}{D}_{2} $ , $ MQ\subset $ 平面 $ {A}_{2}{B}_{2}{C}_{2}{D}_{2} $ ,所以 $ {C}_{1}{C}_{2}\perp MQ $ ,

连接 $ {A}_{2}{C}_{2} $ , $ {A}_{1}{C}_{1} $ , $ {B}_{2}{D}_{2} $ ,因为 $ M $ , $ Q $ 分别为 $ {A}_{2}{D}_{2} $ , $ {A}_{2}{B}_{2} $ 的中点,所以 $ MQ//{B}_{2}{D}_{2} $ .

因为底面 $ {A}_{2}{B}_{2}{C}_{2}{D}_{2} $ 为正方形,所以 $ {A}_{2}{C}_{2}\perp {B}_{2}{D}_{2} $ ,所以 $ {A}_{2}{C}_{2}\perp MQ $ .又 $ {C}_{1}{C}_{2} $ , $ {A}_{2}{C}_{2}\subset $ 平面 $ {A}_{1}{A}_{2}{C}_{2}{C}_{1} $ , $ {C}_{1}{C}_{2}\cap {A}_{2}{C}_{2}={C}_{2} $ ,

所以 $ MQ\perp $ 平面 $ {A}_{1}{A}_{2}{C}_{2}{C}_{1} $ .又 $ {A}_{2}{C}_{1}\subset $ 平面 $ {A}_{1}{A}_{2}{C}_{2}{C}_{1} $ ,所以 $ {A}_{2}{C}_{1}\perp MQ $ ,同理可得 $ {A}_{2}{C}_{1}\perp EQ $ ,

又 $ MQ\cap EQ=Q $ , $ MQ $ , $ EQ\subset $ 平面 $ EMQ $ ,

所以 $ {A}_{2}{C}_{1}\perp $ 平面 $ EMQ $ .

又平面 $ EMQ// $ 平面 $ BCG $ ,所以 $ {A}_{2}{C}_{1}\perp $ 平面 $ BCG $ ,

所以 $ {M}_{1}{N}_{1} $ 的长度即为平面 $ EMQ $ 与平面 $ BCG $ 的距离,则 $ {M}_{1}{N}_{1}={A}_{2}{C}_{1}-{A}_{2}{M}_{1}-{N}_{1}{C}_{1} $ .

由题意得正方体 $ {A}_{2}{B}_{2}{C}_{2}{D}_{2}-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 的棱长为 $ \sqrt{2} $ ,得 $ {A}_{2}{C}_{1}=\sqrt{2+2+2}=\sqrt{6} $ .

由题意得 $ △EMQ $ 为等边三角形,故 $ {S}_{△EMQ}=\dfrac{\sqrt{3}}{4}×{1}^{2}=\dfrac{\sqrt{3}}{4} $ ,

由 $ {V}_{E-{A}_{2}MQ}={V}_{{A}_{2}-EMQ} $ ,得 $ \dfrac{1}{3}×\dfrac{1}{2}×\dfrac{\sqrt{2}}{2}×\dfrac{\sqrt{2}}{2}×\dfrac{\sqrt{2}}{2}=\dfrac{1}{3}×\dfrac{\sqrt{3}}{4}\cdot {A}_{2}{M}_{1} $ ,解得 $ {A}_{2}{M}_{1}=\dfrac{\sqrt{6}}{6} $ .

根据正方体的对称性知 $ {A}_{2}{M}_{1}={N}_{1}{C}_{1} $ ,所以 $ {M}_{1}{N}_{1}={A}_{2}{C}_{1}-{A}_{2}{M}_{1}-{N}_{1}{C}_{1}=\sqrt{6}-2×\dfrac{\sqrt{6}}{6}=\dfrac{2\sqrt{6}}{3} $ ,则平面 $ BCG $ 与平面 $ EMQ $ 之间的距离是 $ \dfrac{2\sqrt{6}}{3} $ .故选 $ \mathrm{D} $ .

如图,取棱 $ AD $ 的中点 $ F $ ,连接 $ BF $ , $ EF $ ,又 $ E $ 是棱 $ {A}_{1}{D}_{1} $ 的中点,所以 $ EF//A{A}_{1} $ ,

因为 $ A{A}_{1}\perp $ 平面 $ ABCD $ ,所以 $ EF\perp $ 平面 $ ABCD $ ,则 $ \mathrm{\angle }EBF $ 是直线 $ BE $ 与平面 $ ABCD $ 所成的角.

设 $ AB=2 $ ,则 $ EF=A{A}_{1}=3 $ , $ AF=1 $ ,又 $ \mathrm{\angle }BAF={120}^{\circ } $ ,在 $ △ABF $ 中,由余弦定理可得 $ BF=\sqrt{A{B}^{2}+A{F}^{2}-2AB\cdot AF \cos \mathrm{\angle }BAF}=\sqrt{7} $ ,则 $ BE=\sqrt{B{F}^{2}+E{F}^{2}}=4 $ ,所以 $ \cos \mathrm{\angle }EBF=\dfrac{BF}{BE}=\dfrac{\sqrt{7}}{4} $ .故选 $ \mathrm{A} $ .

如图,不妨记正四棱台为 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ , $ S $ , $ O $ 分别为上底面和下底面的中心,连接 $ OS $ , $ {A}_{1}S $ , $ AO $ ,

由正四棱台的性质可知 $ OS\perp $ 底面 $ ABCD $ ,过点 $ {A}_{1} $ 作 $ {A}_{1}T\perp AO $ 于点 $ T $ ,易知 $ A $ , $ {A}_{1} $ , $ S $ , $ O $ 四点共面,因为 $ SO\perp $ 底面 $ ABCD $ , $ AO\subset $ 底面 $ ABCD $ ,所以 $ SO\perp AO $ ,所以 $ {A}_{1}T//SO $ ,所以 $ {A}_{1}T\perp $ 底面 $ ABCD $ ,所以 $ \mathrm{\angle }{A}_{1}AT $ 是侧棱与底面所成的角.

因为上、下底面边长分别为2和4,所以 $ {A}_{1}S=\sqrt{2} $ , $ AO=2\sqrt{2} $ ,

所以 $ TO={A}_{1}S=\sqrt{2} $ ,所以 $ AT=AO-OT=\sqrt{2} $ ,所以 $ \tan \mathrm{\angle }{A}_{1}AT=\dfrac{{A}_{1}T}{AT} $ .因为侧棱与底面所成的角为 $ {60}^{\circ } $ ,所以 $ \mathrm{\angle }{A}_{1}AT={60}^{\circ } $ ,故 $ {A}_{1}T=\sqrt{3}AT=\sqrt{6} $ ,

则该正四棱台的体积为 $ \dfrac{1}{3}×({2}^{2}+{4}^{2}+\sqrt{{2}^{2}×{4}^{2}})×\sqrt{6}=\dfrac{28\sqrt{6}}{3} $ .故选 $ \mathrm{A} $ .

如图,在平面 $ ABC $ 内作 $ MG\perp BC $ ,垂足为 $ G $ ,连接 $ NG $ .

在正三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 中, $ {B}_{1}B\perp $ 平面 $ ABC $ ,又 $ MG\subset $ 平面 $ ABC $ ,所以 $ {B}_{1}B\perp MG $ .又 $ MG\perp BC $ , $ BC\cap {B}_{1}B=B $ , $ BC $ , $ {B}_{1}B\subset $ 平面 $ BC{C}_{1}{B}_{1} $ ,所以 $ MG\perp $ 平面 $ BC{C}_{1}{B}_{1} $ ,故 $ \mathrm{\angle }MNG $ 为直线 $ MN $ 与平面 $ BC{C}_{1}{B}_{1} $ 所成的角.当 $ \mathrm{\angle }MNG $ 取得最大值时, $ \tan \mathrm{\angle }MNG=\dfrac{MG}{NG} $ 取得最大值, $ NG $ 取得最小值.

不妨设 $ A{A}_{1}=AB=a $ ,则 $ MG=MB \sin B=\dfrac{1}{2}a\cdot \dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{4}a $ , $ NG $ 的最小值为 $ a $ ,

此时 $ \tan \mathrm{\angle }MNG=\dfrac{MG}{NG}=\dfrac{\sqrt{3}}{4} $ .故选 $ \mathrm{D} $ .

如图,取 $ BC $ 的中点 $ E $ ,连接 $ EM $ , $ EN $ ,

$ \because M $ , $ E $ 分别为 $ AB $ , $ BC $ 的中点, $ \therefore ME//AC $ 且 $ ME=\dfrac{1}{2}AC=1 $ ,

同理可得 $ EN//BD $ 且 $ EN=\dfrac{1}{2}BD=\dfrac{\sqrt{2}}{2} $ ,

$ \therefore \mathrm{\angle }MEN $ （或其补角）为异面直线 $ AC $ 与 $ BD $ 所成的角,则 $ \mathrm{\angle }MEN={45}^{\circ } $ 或 $ {135}^{\circ } $ .

在 $ △MEN $ 中, $ EM=1 $ , $ EN=\dfrac{\sqrt{2}}{2} $ ,

若 $ \mathrm{\angle }MEN={45}^{\circ } $ ,则由余弦定理可得 $ MN=\sqrt{E{M}^{2}+E{N}^{2}-2EM\cdot EN \cos {45}^{\circ }} $

$ =\sqrt{{1}^{2}+{\left(\dfrac{\sqrt{2}}{2}\right) ^ {2}}-2×1×\dfrac{\sqrt{2}}{2}×\dfrac{\sqrt{2}}{2}}=\dfrac{\sqrt{2}}{2} $ ；

若 $ \mathrm{\angle }MEN={135}^{\circ } $ ,则由余弦定理可得 $ MN=\sqrt{E{M}^{2}+E{N}^{2}-2EM\cdot EN \cos {135}^{\circ }}= $

$ \sqrt{{1}^{2}+{\left(\dfrac{\sqrt{2}}{2}\right) ^ {2}}-2×1×\dfrac{\sqrt{2}}{2}×(-\dfrac{\sqrt{2}}{2})}=\dfrac{\sqrt{10}}{2} $ .

综上所述, $ MN=\dfrac{\sqrt{2}}{2} $ 或 $ \dfrac{\sqrt{10}}{2} $ .

连接 $ {A}_{1}H $ , $ BH $ , $ DH $ .因为 $ AB=AD=A{A}_{1} $ , $ AH\perp $ 平面 $ {A}_{1}BD $ ,所以 $ \mathrm{R}\mathrm{t}△ABH≌\mathrm{R}\mathrm{t}△ADH≌\mathrm{R}\mathrm{t}△A{A}_{1}H $ ,所以 $ HB=HD=H{A}_{1} $ .又因为 $ △{A}_{1}BD $ 是等边三角形,所以 $ H $ 是 $ △{A}_{1}BD $ 的中心,所以①正确.

在正方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中, $ {A}_{1}{B}_{1}//CD $ ,且 $ {A}_{1}{B}_{1}=CD $ ,所以四边形 $ {A}_{1}{B}_{1}CD $ 是平行四边形,所以 $ {B}_{1}C//{A}_{1}D $ .又因为 $ {A}_{1}D\subset $ 平面 $ {A}_{1}BD $ , $ {B}_{1}C\not\subset $ 平面 $ {A}_{1}BD $ ,所以 $ {B}_{1}C// $ 平面 $ {A}_{1}BD $ .同理可证 $ {B}_{1}{D}_{1}// $ 平面 $ {A}_{1}BD $ .又因为 $ {B}_{1}C\cap {B}_{1}{D}_{1}={B}_{1} $ , $ {B}_{1}C $ , $ {B}_{1}{D}_{1}\subset $ 平面 $ C{B}_{1}{D}_{1} $ ,所以平面 $ C{B}_{1}{D}_{1}// $ 平面 $ {A}_{1}BD $ .又因为 $ AH\perp $ 平面 $ {A}_{1}BD $ ,所以 $ AH\perp $ 平面 $ C{B}_{1}{D}_{1} $ ,所以②正确.

连接 $ A{D}_{1} $ , $ B{C}_{1} $ .因为四边形 $ BC{C}_{1}{B}_{1} $ 是正方形,所以 $ {B}_{1}C\perp B{C}_{1} $ .因为 $ AB\perp $ 平面 $ BC{C}_{1}{B}_{1} $ , $ {B}_{1}C\subset $ 平面 $ BC{C}_{1}{B}_{1} $ ,所以 $ {B}_{1}C\perp AB $ .又因为 $ B{C}_{1}\cap AB=B $ , $ B{C}_{1} $ , $ AB\subset $ 平面 $ AB{C}_{1}{D}_{1} $ ,所以 $ {B}_{1}C\perp $ 平面 $ AB{C}_{1}{D}_{1} $ .又因为 $ A{C}_{1}\subset $ 平面 $ AB{C}_{1}{D}_{1} $ ,所以 $ A{C}_{1}\perp {B}_{1}C $ ,所以直线 $ A{C}_{1} $ 与 $ {B}_{1}C $ 所成的角是 $ {90}^{\circ } $ ,所以③正确.

若 $ \alpha //\beta $ ,则由 $ m\perp $ 平面 $ \alpha $ , $ n\perp $ 平面 $ \beta $ ,可得 $ m//n $ ,

这与 $ m $ , $ n $ 是异面直线矛盾,故 $ \alpha $ 与 $ \beta $ 相交.

设 $ \alpha \cap \beta =a $ ,过空间内一点 $ P $ ,作 $ m^\prime //m $ , $ n^\prime //n $ ,则 $ m^\prime $ 与 $ n^\prime $ 相交, 设 $ m^\prime $ 与 $ n^\prime $ 确定的平面为 $ \gamma $ .因为 $ l\perp m $ , $ l\perp n $ ,所以 $ l\perp m^\prime $ , $ l\perp n^\prime $ ,所以 $ l\perp \gamma $ .

因为 $ m\perp \alpha $ , $ n\perp \beta $ ,所以 $ m^\prime \perp \alpha $ , $ n^\prime \perp \beta $ ,

所以 $ a\perp m^\prime $ , $ a\perp n^\prime $ ,所以 $ a\perp \gamma $ .

又因为 $ l\not\subset \alpha $ , $ l\not\subset \beta $ ,所以 $ l $ 与 $ a $ 不重合,所以 $ l//a $ ,所以 $ l//\alpha $ , $ l//\beta $ .

如图,取 $ P $ , $ Q $ 分别为 $ VC $ , $ AB $ 的中点,

连接 $ PA $ , $ PB $ , $ PQ $ ,在 $ △VBC $ 中,由余弦定理得 $ \cos \mathrm{\angle }VCB=\dfrac{{3}^{2}+{4}^{2}-(2\sqrt{2})^{2}}{2×3×4}=\dfrac{17}{24} $ ,则 $ PB=\sqrt{\dfrac{9}{4}+16-2×\dfrac{3}{2}×4×\dfrac{17}{24}}=\dfrac{\sqrt{39}}{2} $ ,易证 $ △VAC≌△VBC $ ,所以 $ PA=PB=\dfrac{\sqrt{39}}{2} $ ,

在 $ △ABP $ 中, $ PQ < PA=\dfrac{\sqrt{39}}{2} $ .

过点 $ B $ 作 $ BH\perp VC $ 于 $ H $ ,设 $ HP=x $ ,则 $ V{B}^{2}-V{H}^{2}=B{C}^{2}-H{C}^{2} $ ,即 $ B{C}^{2}-V{B}^{2}=H{C}^{2}-V{H}^{2} $ ,得 $ 8=6x $ ,解得 $ x=\dfrac{4}{3} $ .

连接 $ VQ $ , $ CQ $ , $ QH $ ,因为 $ VA=VB $ , $ CA=CB $ , $ Q $ 为 $ AB $ 的中点,所以 $ VQ\perp AB $ , $ CQ\perp AB $ .

因为 $ VQ\cap CQ=Q $ , $ VQ $ , $ CQ\subset $ 平面 $ VCQ $ ,所以 $ AB\perp $ 平面 $ VCQ $ .

又 $ VC\subset $ 平面 $ VCQ $ ,所以 $ VC\perp AB $ .

又 $ AB\cap BH=B $ , $ AB $ , $ BH\subset $ 平面 $ BHQ $ ,所以 $ VC\perp $ 平面 $ BHQ $ .

因为 $ QH\subset $ 平面 $ BHQ $ ,所以 $ QH\perp VC $ ,所以 $ PQ > HP=\dfrac{4}{3} $ .

取 $ BC $ 的中点 $ M $ ,连接 $ PM $ , $ QM $ ,则 $ PM//VB $ , $ QM//CA $ ,所以 $ CA $ 与 $ VB $ 所成的角即为 $ \mathrm{\angle }PMQ $ （或其补角）,

则 $ \cos \mathrm{\angle }PMQ=\dfrac{P{M}^{2}+M{Q}^{2}-P{Q}^{2}}{2PM\cdot MQ}=\dfrac{2+4-P{Q}^{2}}{4\sqrt{2}}=\dfrac{6-P{Q}^{2}}{4\sqrt{2}} $ .

由 $ \dfrac{4}{3} < PQ < \dfrac{\sqrt{39}}{2} $ 知 $ \dfrac{16}{9} < P{Q}^{2} < \dfrac{39}{4} $ ,

于是 $ -\dfrac{15\sqrt{2}}{32} < \cos \mathrm{\angle }PMQ < \dfrac{19\sqrt{2}}{36} $ .

因为异面直线所成角的取值范围为 $ (0,\dfrac{\mathrm{\pi }}{2}] $ ,

所以 $ CA $ 与 $ VB $ 所成角的余弦值的取值范围为 $ [0,\dfrac{19\sqrt{2}}{36}) $ .

如图所示,将直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 补成直四棱柱 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ ,连接 $ A{D}_{1} $ 和 $ {B}_{1}{D}_{1} $ .

因为 $ A{D}_{1}//B{C}_{1} $ ,所以 $ \mathrm{\angle }{B}_{1}A{D}_{1} $ 或其补角为异面直线 $ A{B}_{1} $ 与 $ B{C}_{1} $ 所成的角.

因为 $ AB=2 $ , $ BC=C{C}_{1}=1 $ ,所以 $ A{B}_{1}=\sqrt{5} $ , $ A{D}_{1}=\sqrt{2} $ ,

在 $ △{B}_{1}{D}_{1}{C}_{1} $ 中, $ \mathrm{\angle }{B}_{1}{C}_{1}{D}_{1}={180}^{\circ }-{120}^{\circ }={60}^{\circ } $ , $ {B}_{1}{C}_{1}=1 $ , $ {D}_{1}{C}_{1}=2 $ ,

所以 $ {B}_{1}{D}_{1}=\sqrt{{1}^{2}+{2}^{2}-2×1×2× \cos {60}^{\circ }}=\sqrt{3} $ ,所以在 $ △A{B}_{1}{D}_{1} $ 中, $ \cos \mathrm{\angle }{B}_{1}A{D}_{1}=\dfrac{{B}_{1}{A}^{2}+A{D}_{1}^{2}-{B}_{1}{D}_{1}^{2}}{2{B}_{1}A\cdot A{D}_{1}}=\dfrac{5+2-3}{2×\sqrt{5}×\sqrt{2}}=\dfrac{\sqrt{10}}{5} $ ,故选 $ \mathrm{C} $ .

由已知条件可得 $ △{A}_{1}{B}_{1}{C}_{1} $ 是等腰直角三角形,且 $ {A}_{1}{B}_{1}\perp {A}_{1}{C}_{1} $ ,连接 $ P{A}_{1} $ ,

所以 $ P{A}_{1}=P{B}_{1}=\dfrac{1}{2}{B}_{1}{C}_{1}=\dfrac{\sqrt{2}}{2}{A}_{1}{B}_{1}=\dfrac{\sqrt{2}}{2}AB=2\sqrt{2} $ ,

所以 $ PA=\sqrt{P{\rm A}_{1}^{2}+A{\rm A}_{1}^{2}}=\sqrt{8+16}=2\sqrt{6} $ , $ PB=\sqrt{P{B}_{1}^{2}+B{B}_{1}^{2}}=\sqrt{8+16}=2\sqrt{6} $ .

设 $ P $ 到直线 $ AB $ 的距离为 $ h $ ,则由 $ PA=PB=2\sqrt{6} $ ,

可知 $ h=\sqrt{P{A}^{2}-{\left(\dfrac{1}{2}AB\right) ^ {2}}}=2\sqrt{5} $ .

设所求距离为 $ d $ ,

因为 $ {V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}=3{V}_{P-ABC}=3{V}_{C-ABP} $ ,所以 $ \dfrac{1}{2}AB\cdot AC\cdot A{A}_{1}=3×\dfrac{1}{3}\cdot d\cdot \dfrac{1}{2}\cdot AB\cdot h $ ,解得 $ d=\dfrac{8\sqrt{5}}{5} $ .故选 $ \mathrm{D} $ .

如图,在正方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ 中,取棱 $ AD $ , $ A{A}_{1} $ 的中点分别为 $ E $ , $ F $ ,连接 $ ME $ , $ EF $ , $ FN $ ,

又因为 $ M $ , $ N $ 分别为 $ AC $ , $ {A}_{1}B $ 的中点,

所以 $ ME//CD//AB//NF $ , $ ME=\dfrac{1}{2}CD=\dfrac{1}{2}AB=NF $ .

因此四边形 $ MEFN $ 为平行四边形,则 $ EF//MN $ ,又 $ EF\subset $ 平面 $ AD{D}_{1}{A}_{1} $ , $ MN\not\subset $ 平面 $ AD{D}_{1}{A}_{1} $ ,所以 $ MN// $ 平面 $ AD{D}_{1}{A}_{1} $ , $ \mathrm{A} $ 正确；

因为 $ AB\perp $ 平面 $ AD{D}_{1}{A}_{1} $ , $ EF\subset $ 平面 $ AD{D}_{1}{A}_{1} $ ,所以 $ AB\perp EF $ ,则 $ MN\perp AB $ , $ \mathrm{B} $ 正确；

显然 $ AF\perp $ 平面 $ ABCD $ ,则 $ \mathrm{\angle }FEA $ 是 $ EF $ 与平面 $ ABCD $ 所成的角,又 $ AE=AF $ , $ \mathrm{\angle }EAF={90}^{\circ } $ ,则 $ \mathrm{\angle }FEA={45}^{\circ } $ ,因为 $ EF//MN $ ,所以直线 $ MN $ 与平面 $ ABCD $ 所成的角为 $ {45}^{\circ } $ , $ \mathrm{C} $ 错误；

因为 $ A{A}_{1}//D{D}_{1} $ , $ EF//MN $ ,所以 $ \mathrm{\angle }AFE $ 是异面直线 $ MN $ 与 $ D{D}_{1} $ 所成的角,显然 $ \mathrm{\angle }AFE={45}^{\circ } $ , $ \mathrm{D} $ 正确．故选 $ \mathrm{C} $ ．

设长方体的长、宽、高分别为 $ a $ , $ b $ , $ c $ ,体对角线为 $ AD $ ,如图所示,

由长方体的性质可得体对角线长 $ l=\sqrt{{a}^{2}+{b}^{2}+{c}^{2}} $ .

由 $ AB\perp $ 平面 $ BEDC $ ,可得 $ AD $ 与平面 $ BEDC $ 所成的角为 $ \alpha =\mathrm{\angle }ADB $ ,

所以 $ \cos \alpha =\dfrac{BD}{l} $ ,

同理可得 $ AD $ 与平面 $ ABC $ 所成的角为 $ \beta =\mathrm{\angle }CAD $ ,所以 $ \cos \beta =\dfrac{AC}{l} $ ,

AD与平面 $ ABE $ 所成的角为 $ \gamma =\mathrm{\angle }EAD $ ,所以 $ \cos \gamma =\dfrac{AE}{l} $ ,

所以 $ { \cos }^{2}\alpha +{ \cos }^{2}\beta +{ \cos }^{2}\gamma =\dfrac{B{D}^{2}}{{l}^{2}}+\dfrac{A{C}^{2}}{{l}^{2}}+\dfrac{A{E}^{2}}{{l}^{2}}=\dfrac{{c}^{2}+{b}^{2}+{a}^{2}+{c}^{2}+{a}^{2}+{b}^{2}}{{a}^{2}+{b}^{2}+{c}^{2}}=2 $ .

因为 $ \sin \alpha =\dfrac{\sqrt{2}}{3} $ , $ \alpha \in [0,\dfrac{\mathrm{\pi }}{2}] $ ,所以 $ \cos \alpha =\dfrac{\sqrt{7}}{3} $ ,

又 $ \cos \beta =\dfrac{\sqrt{3}}{3} $ ,则 $ { \cos }^{2}\gamma =2-\dfrac{7}{9}-\dfrac{3}{9}=\dfrac{8}{9} $ .

又因为 $ \gamma \in [0,\dfrac{\mathrm{\pi }}{2}] $ ,所以 $ \cos \gamma =\dfrac{2\sqrt{2}}{3} $ .

故选 $ \mathrm{B} $ .

$ \because $ 在矩形 $ ABCD $ 中, $ AB=2BC $ , $ E $ 为 $ DC $ 的中点,过点 $ E $ 作 $ E{Q}_{2}\perp AB $ 交 $ AB $ 于点 $ {Q}_{2} $ ,

$ \therefore $ 在折起过程中,点 $ D $ 在平面 $ ABCE $ 上的射影点 $ D^\prime $ 在图中线段 $ {Q}_{1}{Q}_{2} $ 上.

$ \because D^\prime E $ 与 $ AC $ 所成角不能为直角,

$ \therefore DE $ 与平面 $ ACD $ 不垂直,故①错误.

只有点 $ D $ 的射影位于 $ {Q}_{2} $ 位置,即平面 $ AED $ 与平面 $ AEB $ 重合时,才有 $ BE\perp CD $ ,此时 $ CD $ 不垂直于平面 $ AECB $ ,即 $ CD $ 与平面 $ BED $ 不垂直,故②错误.

$ \because BD\prime $ 与 $ AC $ 所成角不能为直角,

$ \therefore BD $ 不能垂直于平面 $ ACD $ ,故③错误.

$ \because AD\perp DE $ ,并且在折起过程中,存在一个位置使 $ AD\prime \perp BE $ , $ \therefore $ 存在一个位置使 $ AD\perp BE $ ,又 $ BE\cap DE=E $ , $ BE $ , $ DE\subset $ 平面 $ BED $ , $ \therefore $ 在折起过程中有 $ AD\perp $ 平面 $ BED $ ,故④正确.故选 $ \mathrm{A} $ .

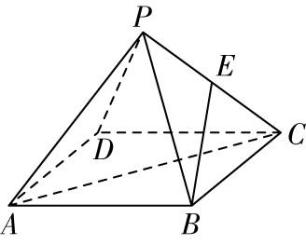
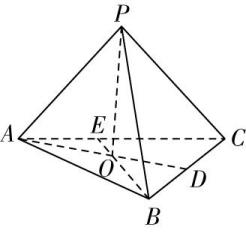
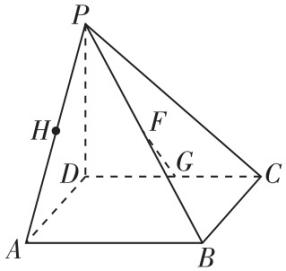
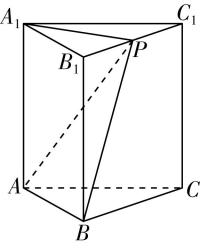
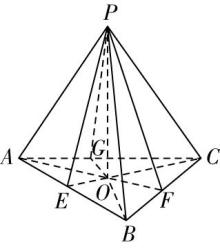
如图,连接 $ PG $ 并延长,交 $ BC $ 于点 $ D $ ,连接 $ AD $ ,

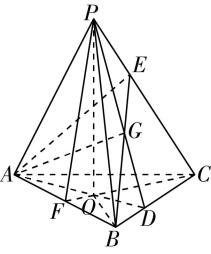
因为 $ G $ 为 $ △PBC $ 的垂心,所以 $ BC\perp PD $ ,

因为 $ AG\perp $ 平面 $ PBC $ , $ BC\subset $ 平面 $ PBC $ ,所以 $ BC\perp AG $ ,

又 $ AG\cap PD=G $ , $ AG $ , $ PD\subset $ 平面 $ PAD $ ,所以 $ BC\perp $ 平面 $ PAD $ .

因为 $ AD\subset $ 平面 $ PAD $ ,所以 $ BC\perp AD $ .

连接 $ BG $ 并延长,交 $ PC $ 于点 $ E $ ,连接 $ AE $ ,

因为 $ AG\perp $ 平面 $ PBC $ , $ PC\subset $ 平面 $ PBC $ ,所以 $ AG\perp PC $ ,

因为 $ G $ 为 $ △PBC $ 的垂心,所以 $ BE\perp PC $ ,又 $ AG\cap BE=G $ , $ AG $ , $ BE\subset $ 平面 $ ABE $ ,所以 $ PC\perp $ 平面 $ ABE $ .

因为 $ AB\subset $ 平面 $ ABE $ ,所以 $ AB\perp PC $ ,

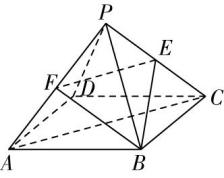
设点 $ P $ 在平面 $ ABC $ 内的射影为点 $ O $ ,连接 $ CO $ 并延长,交 $ AB $ 于点 $ F $ ,连接 $ PF $ , $ OB $ ,

因为 $ PO\perp $ 平面 $ ABC $ , $ AB\subset $ 平面 $ ABC $ ,所以 $ PO\perp AB $ ,

又 $ PO\cap PC=P $ , $ PO $ , $ PC\subset $ 平面 $ PCF $ ,所以 $ AB\perp $ 平面 $ PCF $ ,

因为 $ CF\subset $ 平面 $ PCF $ ,所以 $ CF\perp AB $ .

因为 $ AD\cap CF=O $ ,所以 $ O $ 为正三角形 $ ABC $ 的中心,且 $ F $ 为 $ AB $ 的中点.

因为 $ PO\perp $ 平面 $ ABC $ , $ OA $ , $ OB $ , $ OC\subset $ 平面 $ ABC $ ,所以 $ PO\perp OA $ , $ PO\perp OB $ , $ PO\perp OC $ ,

又 $ OA=OB=OC $ ,

所以 $ △POA≌△POB≌△POC $ ,所以 $ PA=PB=PC $ .

由三角形的面积公式有 $ {S}_{△PBC}=\dfrac{1}{2}\cdot BP\cdot PC\cdot \sin \mathrm{\angle }BPC $ ,

当 $ \sin \mathrm{\angle }BPC=1 $ 时, $ {S}_{△PBC} $ 最大,此时 $ PB\perp PC $ ,

所以当 $ PB\perp PC $ 时, $ △PBC $ 的面积取最大值,

当 $ PA\perp PB $ , $ PA\perp PC $ 时,又 $ PB\cap PC=P $ , $ PB $ , $ PC\subset $ 平面 $ PBC $ ,

所以 $ PA\perp $ 平面 $ PBC $ ,

此时 $ {V}_{P-ABC}=\dfrac{1}{3}{S}_{△PBC}\cdot PA $ ,当 $ PA $ 与 $ PB $ , $ PC $ 不垂直时,此时高一定比 $ PA $ 小,

所以当 $ PB\perp PC $ , $ PA\perp PB $ , $ PA\perp PC $ 时,三棱锥 $ P-ABC $ 的体积最大.

又 $ PA\perp PB $ ,底面是边长为3的正三角形,

由等腰直角三角形性质得 $ \sqrt{2}PA=AB=3 $ ,解得 $ PA=\dfrac{3\sqrt{2}}{2} $ .故选 $ \mathrm{C} $ .

对于 $ \mathrm{A} $ 选项,如图,连接 $ OA $ , $ OB $ , $ OC $ ,因为 $ PO\perp $ 平面 $ ABC $ , $ OA $ , $ OB $ , $ OC\subset $ 平面 $ ABC $ ,所以 $ PO\perp OA $ , $ PO\perp OB $ , $ PO\perp OC $ .因为 $ PA=PB=PC $ ,所以 $ \sqrt{P{A}^{2}-P{O}^{2}}=\sqrt{P{B}^{2}-P{O}^{2}}=\sqrt{P{C}^{2}-P{O}^{2}} $ ,

所以 $ OA=OB=OC $ ,所以点 $ O $ 是 $ △ABC $ 的外心, $ \mathrm{A} $ 错误.

对于 $ \mathrm{B} $ 选项,如图,过点 $ P $ 在平面 $ PAB $ 内作 $ PE\perp AB $ ,垂足为点 $ E $ ,过点 $ P $ 在平面 $ PBC $ 内作 $ PF\perp BC $ ,垂足为点 $ F $ ,过点 $ P $ 在平面 $ PAC $ 内作 $ PG\perp AC $ ,垂足为点 $ G $ ,连接 $ OE $ , $ OF $ , $ OG $ ,

因为 $ PO\perp $ 平面 $ ABC $ , $ OE $ , $ AB\subset $ 平面 $ ABC $ ,所以 $ AB\perp PO $ , $ OE\perp PO $ ,

又因为 $ PE\perp AB $ , $ PO\cap PE=P $ , $ PO $ , $ PE\subset $ 平面 $ POE $ ,所以 $ AB\perp $ 平面 $ POE $ .

又因为 $ OE\subset $ 平面 $ POE $ ,所以 $ OE\perp AB $ ,

$ OE=\sqrt{P{E}^{2}-P{O}^{2}} $ ,同理可知, $ OF\perp BC $ , $ OG\perp AC $ ,且 $ OF=\sqrt{P{F}^{2}-P{O}^{2}} $ , $ OG=\sqrt{P{G}^{2}-P{O}^{2}} $ ,

由题意知 $ PE=PF=PG $ ,所以 $ OE=OF=OG $ ,所以点 $ O $ 是 $ △ABC $ 的内心, $ \mathrm{B} $ 正确.

对于 $ \mathrm{C} $ 选项,若 $ PA\perp BC $ , $ PB\perp AC $ ,因为 $ PO\perp $ 平面 $ ABC $ , $ BC\subset $ 平面 $ ABC $ ,所以 $ PO\perp BC $ ,又 $ PA\cap PO=P $ , $ PA $ , $ PO\subset $ 平面 $ PAO $ ,所以 $ BC\perp $ 平面 $ PAO $ .因为 $ AO\subset $ 平面 $ PAO $ ,所以 $ BC\perp AO $ ,同理可得 $ AC\perp BO $ ,故 $ \overrightarrow {OA}\cdot \overrightarrow {BC}=0 $ , $ \overrightarrow {OB}\cdot \overrightarrow {AC}=0 $ ,即 $ \overrightarrow {OA}\cdot (\overrightarrow {OC}-\overrightarrow {OB})=0 $ , $ \overrightarrow {OB}\cdot (\overrightarrow {OC}-\overrightarrow {OA})=0 $ ,所以 $ \overrightarrow {OA}\cdot \overrightarrow {OB}=\overrightarrow {OB}\cdot \overrightarrow {OC}=\overrightarrow {OC}\cdot \overrightarrow {OA} $ ,所以 $ \overrightarrow {OC}\cdot (\overrightarrow {OA}-\overrightarrow {OB})=\overrightarrow {OC}\cdot \overrightarrow {BA}=0 $ ,即 $ OC\perp AB $ ,所以点 $ O $ 是 $ △ABC $ 的垂心, $ \mathrm{C} $ 正确.

对于 $ \mathrm{D} $ 选项,因为 $ PO\perp $ 平面 $ ABC $ ,所以 $ PA $ , $ PB $ , $ PC $ 与平面 $ ABC $ 所成的角分别为 $ \mathrm{\angle }PAO $ , $ \mathrm{\angle }PBO $ , $ \mathrm{\angle }PCO $ ,

由题意可知, $ \mathrm{\angle }PAO=\mathrm{\angle }PBO=\mathrm{\angle }PCO $ ,所以 $ \dfrac{PO}{ \tan \mathrm{\angle }PAO}=\dfrac{PO}{ \tan \mathrm{\angle }PBO}=\dfrac{PO}{ \tan \mathrm{\angle }PCO} $ ,

即 $ OA=OB=OC $ ,所以点 $ O $ 是 $ △ABC $ 的外心, $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .