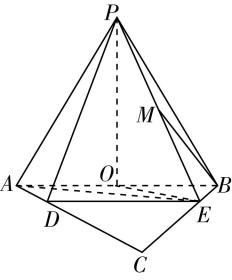
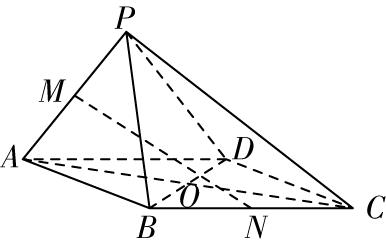
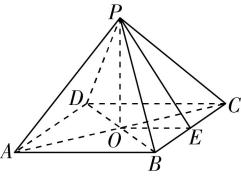
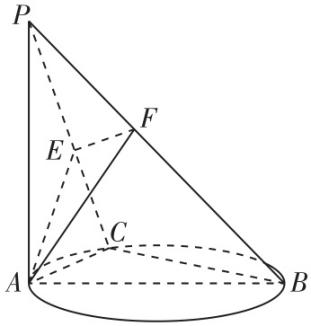
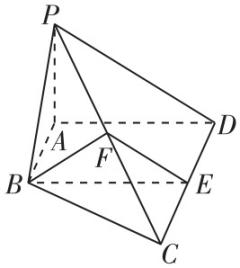
5.如图,在四棱锥 $ P-ABCD $ 中,底面 $ ABCD $ 是边长为3的菱形,且 $ \mathrm{\angle }DAB={60}^{\circ } $ , $ AC $ 交 $ BD $ 于点 $ O $ , $ PB=PD=3 $ , $ PA\perp PC $ , $ M $ , $ N $ 分别为 $ PA $ , $ BC $ 的中点.
(1) 求证: $ MN// $ 平面 $ PCD $ .
(2) 记二面角 $ B-PC-D $ 的平面角为 $ \theta $ ,若 $ \cos \theta =-\dfrac{1}{7} $ .
② 求点 $ N $ 到平面 $ CDP $ 的距离.
答案:(1) 【证明】如图,取 $ PD $ 的中点 $ E $ ,连接 $ ME $ , $ CE $ ,
因为 $ M $ 为 $ PA $ 的中点,所以 $ ME=\dfrac{1}{2}AD $ , $ ME//AD $ .
又因为 $ N $ 为 $ BC $ 的中点且四边形 $ ABCD $ 为菱形,所以 $ NC//AD $ , $ NC=\dfrac{1}{2}AD $ ,
所以 $ NC//ME $ , $ NC=ME $ ,所以四边形 $ MNCE $ 为平行四边形,所以 $ MN//CE $ .
因为 $ MN\not\subset $ 平面 $ PCD $ , $ CE\subset $ 平面 $ PCD $ ,所以 $ MN// $ 平面 $ PCD $ .

(2) ① 【解】取 $ PC $ 的中点 $ F $ ,连接 $ DF $ , $ BF $ , $ PO $ ,
因为 $ PB=PD=BC=CD=3 $ ,
所以 $ △BPC≌△DPC $ ,且 $ DF\perp PC $ , $ BF\perp PC $ , $ DF=BF $ ,
所以 $ \mathrm{\angle }BFD $ 为二面角 $ B-PC-D $ 的平面角,即 $ \cos \mathrm{\angle }BFD= \cos \theta =-\dfrac{1}{7} $ ,
在 $ △BFD $ 中,由余弦定理可得 $ B{D}^{2}=B{F}^{2}+D{F}^{2}-2BF\cdot DF \cos \mathrm{\angle }BFD $ ,
因为底面 $ ABCD $ 是边长为3的菱形,且 $ \mathrm{\angle }DAB={60}^{\circ } $ ,所以 $ △ABD $ 为等边三角形,所以 $ BD=3 $ ,则 $ 9=B{F}^{2}+B{F}^{2}-2B{F}^{2}×(-\dfrac{1}{7}) $ ,解得 $ BF=\dfrac{3\sqrt{7}}{4} $ ,
则 $ PC=2\sqrt{B{C}^{2}-B{F}^{2}}=2\sqrt{9-\dfrac{63}{16}}=\dfrac{9}{2} $ .
因为 $ PB=PD $ , $ O $ 是 $ BD $ 的中点,所以 $ PO\perp BD $ .
又因为四边形 $ ABCD $ 为菱形,所以 $ AC\perp BD $ ,
由 $ PO\cap AC=O $ , $ PO $ , $ AC\subset $ 平面 $ PAC $ ,可得 $ BD\perp $ 平面 $ PAC $ .
由 $ BD\subset $ 平面 $ ABCD $ ,可知平面 $ PAC\perp $ 平面 $ ABCD $ ,且平面 $ PAC\cap $ 平面 $ ABCD=AC $ ,
由面面垂直的性质可知直线 $ PA $ 在平面 $ ABCD $ 上的射影为 $ AC $ ,
所以 $ PA $ 与底面 $ ABCD $ 所成角为 $ \mathrm{\angle }PAC $ .
因为 $ PA\perp PC $ ,所以 $ \sin \mathrm{\angle }PAC=\dfrac{PC}{AC}=\dfrac{PC}{2OC}=\dfrac{\dfrac{9}{2}}{3\sqrt{3}}=\dfrac{\sqrt{3}}{2} $ .
由 $ {0}^{\circ } < \mathrm{\angle }PAC < {90}^{\circ } $ ,可知 $ \mathrm{\angle }PAC={60}^{\circ } $ ,
所以 $ PA $ 与底面 $ ABCD $ 所成角的大小为 $ {60}^{\circ } $ .
② 如图,连接 $ OF $ , $ ON $ ,过 $ O $ 作 $ OG\perp DF $ 于 $ G $ ,
因为 $ O $ , $ N $ 分别为 $ BD $ , $ BC $ 的中点,所以 $ ON//CD $ .又 $ ON\not\subset $ 平面 $ CDP $ , $ CD\subset $ 平面 $ CDP $ ,则 $ ON// $ 平面 $ CDP $ ,
则点 $ N $ 到平面 $ CDP $ 的距离即为点 $ O $ 到平面 $ CDP $ 的距离.
因为 $ BF\perp PC $ , $ DF\perp PC $ , $ BF\cap DF=F $ , $ BF $ , $ DF\subset $ 平面 $ BFD $ ,所以 $ PC\perp $ 平面 $ BFD $ .
因为 $ PC\subset $ 平面 $ CDP $ ,所以平面 $ CDP\perp $ 平面 $ BDF $ .
又因为 $ OG\perp DF $ , $ OG\subset $ 平面 $ BDF $ ,平面 $ CDP\cap $ 平面 $ BDF=DF $ ,
所以 $ OG\perp $ 平面 $ CDP $ .
在 $ △OFD $ 中, $ OF=\dfrac{1}{2}AP=\dfrac{1}{2}\sqrt{A{C}^{2}-P{C}^{2}}=\dfrac{3\sqrt{3}}{4} $ , $ OD=\dfrac{3}{2} $ , $ DF=BF=\dfrac{3\sqrt{7}}{4} $ ,则有 $ O{F}^{2}+O{D}^{2}=D{F}^{2} $ ,所以 $ OF\perp OD $ .
所以由等面积法可得 $ \dfrac{1}{2}OF\cdot OD=\dfrac{1}{2}DF\cdot OG $ ,即 $ OG=\dfrac{OF\cdot OD}{DF}=\dfrac{\dfrac{3\sqrt{3}}{4}×\dfrac{3}{2}}{\dfrac{3\sqrt{7}}{4}}=\dfrac{3\sqrt{21}}{14} $ ,
所以点 $ N $ 到平面 $ CDP $ 的距离为 $ \dfrac{3\sqrt{21}}{14} $ .
 (多选)
(多选)


 (多选)
(多选)
 (多选)
(多选)