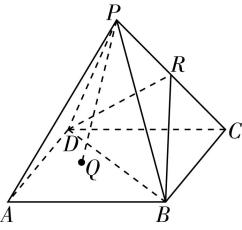
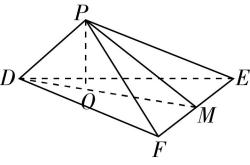
11.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马 $ P-ABCD $ 中,侧棱 $ PD\perp $ 底面 $ ABCD $ ,且 $ PD=CD=2 $ ,点 $ E $ 是 $ PC $ 的中点,连接 $ DE $ , $ BD $ , $ BE $ .
(1) 证明: $ DE\perp $ 平面 $ PBC $ .试判断四面体 $ EBCD $ 是否为鳖臑.若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.
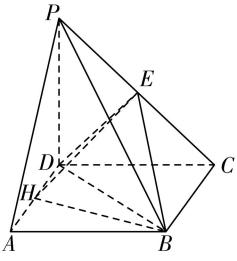
(2) 设点 $ H $ 是 $ AD $ 的中点,若二面角 $ E-BD-C $ 的大小为 $ \dfrac{\mathrm{\pi }}{3} $ ,求三棱锥 $ E-HBD $ 的外接球的表面积.
答案:(1) 【解】因为 $ PD\perp $ 底面 $ ABCD $ , $ BC\subset $ 底面 $ ABCD $ ,所以 $ PD\perp BC $ .
因为底面 $ ABCD $ 为长方形,
所以 $ BC\perp CD $ .
因为 $ PD\cap CD=D $ , $ PD $ , $ CD\subset $ 平面 $ PCD $ ,
所以 $ BC\perp $ 平面 $ PCD $ .
因为 $ DE\subset $ 平面 $ PCD $ , $ PC\subset $ 平面 $ PCD $ ,
所以 $ BC\perp DE $ , $ BC\perp PC $ .
因为 $ PD=CD $ ,点 $ E $ 是 $ PC $ 的中点,
所以 $ DE\perp PC $ .
因为 $ PC\cap BC=C $ , $ PC $ , $ BC\subset $ 平面 $ PBC $ ,
所以 $ DE\perp $ 平面 $ PBC $ .
因为 $ EB\subset $ 平面 $ PBC $ ,所以 $ DE\perp EB $ ,
所以四面体 $ EBCD $ 的四个面都是直角三角形,即四面体 $ EBCD $ 是一个鳖臑, 其四个面的直角分别是 $ \mathrm{\angle }BCD $ , $ \mathrm{\angle }BCE $ , $ \mathrm{\angle }DEC $ , $ \mathrm{\angle }DEB $ .
(2) 如图①,取 $ DC $ 的中点 $ F $ ,连接 $ EF $ ,过点 $ F $ 作 $ FG\perp BD $ 于点 $ G $ ,连接 $ EG $ .

图①
因为 $ E $ , $ F $ 分别是 $ PC $ , $ DC $ 的中点,所以 $ EF//PD $ ,
又 $ PD\perp $ 底面 $ ABCD $ ,所以 $ EF\perp $ 平面 $ ABCD $ .因为 $ BD $ , $ FG\subset $ 平面 $ ABCD $ ,
所以 $ EF\perp BD $ , $ EF\perp FG $ .
又因为 $ FG\perp BD $ , $ EF\cap FG=F $ , $ EF $ , $ FG\subset $ 平面 $ EFG $ ,
所以 $ BD\perp $ 平面 $ EFG $ .因为 $ EG\subset $ 平面 $ EFG $ ,所以 $ BD\perp EG $ ,所以 $ \mathrm{\angle }EGF $ 就是二面角 $ E-BD-C $ 的平面角,所以 $ \mathrm{\angle }EGF=\dfrac{\mathrm{\pi }}{3} $ .
设 $ AD=t $ ,
由 $ \mathrm{\angle }FGD=\mathrm{\angle }BCD=\dfrac{\mathrm{\pi }}{2} $ ,可知 $ △DFG\sim △DBC $ ,所以 $ \dfrac{DF}{BD}=\dfrac{FG}{BC} $ ,所以 $ FG=\dfrac{t}{\sqrt{{t}^{2}+4}} $ ,所以 $ \tan \mathrm{\angle }EGF=\dfrac{EF}{FG}=\sqrt{3} $ ,又 $ EF=\dfrac{1}{2}PD=1 $ ,所以 $ FG=\dfrac{\sqrt{3}}{3} $ ,
所以 $ \dfrac{t}{\sqrt{{t}^{2}+4}}=\dfrac{\sqrt{3}}{3} $ ,解得 $ t=\sqrt{2} $ .
因为 $ CD=2 $ , $ AD=\sqrt{2} $ ,所以 $ BD=\sqrt{6} $ , $ DH=\dfrac{\sqrt{2}}{2} $ ,所以 $ HB=\sqrt{A{H}^{2}+A{B}^{2}}=\dfrac{3\sqrt{2}}{2} $ ,
所以 $ \cos \mathrm{\angle }DHB=\dfrac{D{H}^{2}+H{B}^{2}-B{D}^{2}}{2\cdot DH\cdot HB}=-\dfrac{1}{3} $ ,所以 $ \sin \mathrm{\angle }DHB=\dfrac{2\sqrt{2}}{3} $ .
如图②,设 $ △DHB $ 的外接圆半径为 $ r $ ,外接圆圆心为 $ O $ ,连接 $ OB $ , $ OD $ , $ OH $ ,

图②
则 $ 2r=\dfrac{BD}{ \sin \mathrm{\angle }DHB}=\dfrac{3\sqrt{3}}{2} $ ,则 $ r=DO=HO=BO=\dfrac{3\sqrt{3}}{4} $ ,
在底面 $ ABCD $ 中,过点 $ O $ 作 $ OM\perp CD $ , $ OK\perp DH $ ,垂足分别为 $ M $ , $ K $ ,连接 $ OF $ ,
则 $ OM=DK=\dfrac{1}{2}DH=\dfrac{\sqrt{2}}{4} $ ,则 $ DM=\sqrt{D{O}^{2}-O{M}^{2}}=\dfrac{5}{4} $ ,
又 $ DF=1 $ ,所以 $ FM=\dfrac{1}{4} $ ,所以 $ FO=\dfrac{\sqrt{3}}{4} $ .
设三棱锥 $ E-HBD $ 的外接球球心为 $ {O}_{1} $ ,球的半径为 $ R $ ,连接 $ O{O}_{1} $ ,并设 $ O{O}_{1}=\lambda (\lambda > 0) $ ,
若球心 $ {O}_{1} $ 和点 $ E $ 位于平面 $ DHB $ 的异侧,如图③,连接 $ {O}_{1}H $ , $ {O}_{1}E $ ,

图③
则 $ R=H{O}_{1}=\sqrt{{\left(\dfrac{3\sqrt{3}}{4}\right) ^ {2}}+{\lambda }^{2}}=E{O}_{1}=\sqrt{{\left(\dfrac{\sqrt{3}}{4}\right) ^ {2}}+{\left(\lambda +1\right) ^ {2}}} $ ,解得 $ \lambda =\dfrac{1}{4} $ ,
则 $ R=\dfrac{\sqrt{7}}{2} $ .
若球心 $ {O}_{1} $ 和点 $ E $ 位于平面 $ DHB $ 同侧,则 $ R=H{O}_{1}=\sqrt{{\left(\dfrac{3\sqrt{3}}{4}\right) ^ {2}}+{\lambda }^{2}}=E{O}_{1}=\sqrt{{\left(\dfrac{\sqrt{3}}{4}\right) ^ {2}}+{\left(1-\lambda \right) ^ {2}}} $ ,解得 $ \lambda =-\dfrac{1}{4} $ (舍去).
综上,三棱锥 $ E-HBD $ 的外接球的表面积 $ S=4\mathrm{\pi }{R}^{2}=7\mathrm{\pi } $ .

 (多选)
(多选) (多选)
(多选)