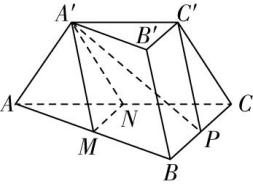
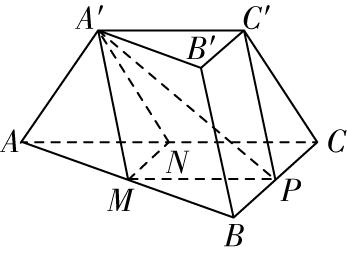
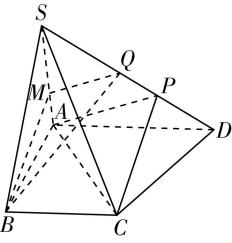
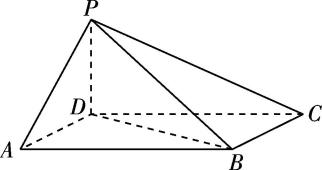
2.(多选)已知三棱台 $ ABC-{A}^{\prime }{B}^{\prime }{C}^{\prime } $ ,上、下底面边长之比为 $ 1:2 $ ,棱 $ AB $ , $ BC $ , $ AC $ 的中点分别为点 $ M $ , $ P $ , $ N $ ,则下列结论错误的有( )
 (多选)
(多选)
A. $ {A}^{\prime }N//{PC}^{\prime } $
B. $ {A}^{\prime }P $ 与 $ AC $ 为异面直线
C. $ AB// $ 平面 $ {A}^{\prime }{C}^{\prime }P $
D.平面 $ {A}^{\prime }MN// $ 平面 $ {BCC}^{\prime }{B}^{\prime } $
对于 $ \mathrm{A} $ ,因为 $ A^\prime N\subset $ 平面 $ A^\prime C^\prime CA $ , $ C^\prime \in $ 平面 $ A^\prime C^\prime CA $ , $ P\notin $ 平面 $ A^\prime C^\prime CA $ ,
且 $ C^\prime \notin A^\prime N $ ,所以 $ A^\prime N $ , $ PC\prime $ 为异面直线,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,因为 $ AC\subset $ 平面 $ A^\prime C^\prime CA $ , $ A^\prime \in $ 平面 $ A^\prime C^\prime CA $ , $ P\notin $ 平面 $ A^\prime C^\prime CA $ ,且 $ A^\prime \notin AC $ ,所以 $ A^\prime P $ 与 $ AC $ 为异面直线,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,如图,连接 $ MP $ ,因为棱 $ AB $ , $ BC $ 的中点分别为点 $ M $ , $ P $ ,所以 $ AC//MP $ ,因为 $ AC//A^\prime C^\prime $ ,所以 $ MP//A^\prime C^\prime $ ,所以 $ M $ , $ P $ , $ C^\prime $ , $ A^\prime $ 四点共面,又 $ AB\cap $ 平面 $ A^\prime C^\prime PM=M $ ,所以 $ AB $ 与平面 $ A^\prime C^\prime P $ 不平行,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,因为 $ AB $ , $ AC $ 的中点分别为点 $ M $ , $ N $ ,所以 $ MN//BC $ ,因为 $ MN\not\subset $ 平面 $ BCC\prime B^\prime $ , $ BC\subset $ 平面 $ BCC\prime B^\prime $ ,所以 $ MN// $ 平面 $ BCC\prime B^\prime $ ,
因为 $ AC//A^\prime C^\prime $ , $ A^\prime C^\prime =\dfrac{1}{2}AC=NC $ ,所以四边形 $ A^\prime C^\prime CN $ 为平行四边形,所以 $ A^\prime N//C^\prime C $ ,因为 $ A^\prime N\not\subset $ 平面 $ BCC\prime B^\prime $ , $ C^\prime C\subset $ 平面 $ BCC\prime B^\prime $ ,所以 $ A^\prime N// $ 平面 $ BCC\prime B^\prime $ ,又 $ MN\cap A^\prime N=N $ , $ MN $ , $ A^\prime N\subset $ 平面 $ A^\prime MN $ ,所以平面 $ A^\prime MN// $ 平面 $ BCC\prime B^\prime $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C} $ .



 (多选)
(多选) (多选)
(多选)