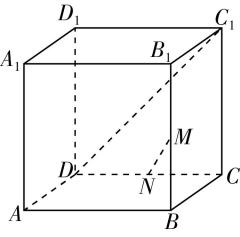
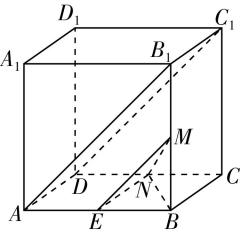
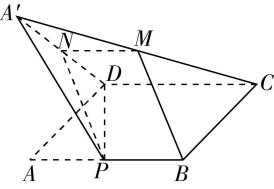
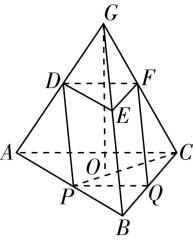
4.如图,四棱锥 $ P-ABCD $ 的各个顶点均在球 $ \mathrm{O} $ 的表面上,且 $ AB=AD=2 $ , $ BC\perp CD $ , $ PB\perp $ 平面 $ PAD $ .
(3) 当 $ 5PA\cdot PB=6\sqrt{2} $ 时,求直线 $ PC $ 与平面 $ ABCD $ 所成角的余弦值的最大值.
答案:(1) 【证明】由题知四边形 $ ABCD $ 在球 $ O $ 的一个截面的圆周上,故 $ \mathrm{\angle }BAD+\mathrm{\angle }BCD=\mathrm{\pi } $ ,
又 $ BC\perp CD $ ,故 $ \mathrm{\angle }BAD=\dfrac{\mathrm{\pi }}{2} $ ,故 $ AB\perp AD $ ,
由 $ PB\perp $ 平面 $ PAD $ , $ AD\subset $ 平面 $ PAD $ ,得 $ PB\perp AD. $
又 $ AB\cap PB=B $ , $ AB\subset $ 平面 $ PAB $ , $ PB\subset $ 平面 $ PAB $ ,故 $ AD\perp $ 平面 $ PAB $ ,
又 $ AD\subset $ 平面 $ ABCD $ ,故平面 $ PAB\perp $ 平面 $ ABCD $ .
(2) 【解】如图,过点 $ P $ 在平面 $ PAB $ 内作 $ PH\perp AB $ ,垂足为点 $ H $ ,连接 $ BD $ ,
由平面 $ PAB\perp $ 平面 $ ABCD $ ,平面 $ PAB\cap $ 平面 $ ABCD=AB $ , $ PH\subset $ 平面 $ PAB $ ,可得 $ PH\perp $ 平面 $ ABCD $ .
记四棱锥 $ P-ABCD $ 的体积为 $ V $ ,
则 $ V=\dfrac{1}{3}\cdot PH\cdot {S}_{四边形ABCD}=\dfrac{1}{3}\cdot PH\cdot ({S}_{△ABD}+{S}_{△BCD}) $ .
因为 $ AB\perp AD $ ,所以 $ {S}_{△ABD}=\dfrac{1}{2}\cdot AB\cdot AD=\dfrac{1}{2}×2×2=2 $ ,
由 $ PB\perp $ 平面 $ PAD $ , $ PA\subset $ 平面 $ PAD $ ,得 $ PB\perp PA $ ,故 $ P{B}^{2}+P{A}^{2}=A{B}^{2}=4 $ ,
于是 $ PA\cdot PB\leqslant \dfrac{P{A}^{2}+P{B}^{2}}{2}=2 $ ,当且仅当 $ PA=PB=\sqrt{2} $ 时取等号,
在 $ \mathrm{R}\mathrm{t}△ABP $ 中,由等面积法可得 $ PH=\dfrac{PA\cdot PB}{AB}\leqslant \dfrac{2}{2}=1 $ .
由 $ BC\perp CD $ ,得 $ 8=B{D}^{2}=B{C}^{2}+C{D}^{2}\geqslant 2BC\cdot CD $ ,
故 $ BC\cdot CD\leqslant 4 $ ,当且仅当 $ BC=CD=2 $ 时取等号,于是 $ {S}_{△BCD}=\dfrac{1}{2}\cdot BC\cdot CD\leqslant 2 $ .
故 $ V=\dfrac{1}{3}\cdot PH\cdot ({S}_{△ABD}+{S}_{△BCD})\leqslant \dfrac{1}{3}×1×(2+2)=\dfrac{4}{3} $ ,当且仅当 $ PA=PB=\sqrt{2} $ , $ BC=DC=2 $ 时取等号,
故四棱锥 $ P-ABCD $ 体积的最大值为 $ \dfrac{4}{3} $ .

(3) 【解】如图,取线段 $ BD $ 的中点 $ O $ ,连接 $ HO $ , $ OC $ ,
因为 $ BC\perp CD $ , $ O $ 为 $ BD $ 的中点,所以 $ OC=\dfrac{1}{2}BD=\dfrac{1}{2}\sqrt{A{B}^{2}+A{D}^{2}}=\dfrac{1}{2}×2\sqrt{2}=\sqrt{2} $ .
因为 $ PA\perp PB $ , $ PA\cdot PB=\dfrac{6\sqrt{2}}{5} $ , $ AB=2 $ ,在 $ \mathrm{R}\mathrm{t}△ABP $ 中,由等面积法知 $ PH=\dfrac{PA\cdot PB}{AB}=\dfrac{3\sqrt{2}}{5} $ ,
联立可得 $ \begin{cases}PA\cdot PB=\dfrac{6\sqrt{2}}{5},\\ P{A}^{2}+P{B}^{2}=A{B}^{2}=4,\end{cases} $ 设 $ PB=m $ ,则 $ PA=\dfrac{6\sqrt{2}}{5m} $ ,
所以 $ P{A}^{2}+P{B}^{2}={\left(\dfrac{6\sqrt{2}}{5m}\right) ^ {2}}+{m}^{2}=4 $ ,整理得 $ 25{m}^{4}-100{m}^{2}+72=0 $ ,
解得 $ {m}^{2}=\dfrac{10±2\sqrt{7}}{5} $ ,即 $ P{B}^{2}=\dfrac{10±2\sqrt{7}}{5} $ .
因为 $ PH\perp AB $ , $ PA\perp PB $ ,所以 $ \cos \mathrm{\angle }PBA=\dfrac{BH}{PB}=\dfrac{PB}{AB} $ ,故 $ BH=\dfrac{P{B}^{2}}{AB}=\dfrac{{m}^{2}}{2} $ ,
在 $ △BHO $ 中, $ OB=\sqrt{2} $ , $ \mathrm{\angle }OBH=\dfrac{\mathrm{\pi }}{4} $ ,
由余弦定理可得 $ O{H}^{2}=B{H}^{2}+O{B}^{2}-2BH\cdot OB \cos \dfrac{\mathrm{\pi }}{4}=B{H}^{2}+2-2BH $ ,
当 $ {m}^{2}=\dfrac{10+2\sqrt{7}}{5} $ 时, $ BH=\dfrac{{m}^{2}}{2}=\dfrac{5+\sqrt{7}}{5} $ ,
此时 $ O{H}^{2}=B{H}^{2}+2-2BH=\dfrac{32+10\sqrt{7}}{25}+2-2×\dfrac{5+\sqrt{7}}{5}=\dfrac{32}{25} $ ,此时 $ OH=\dfrac{4\sqrt{2}}{5} $ ;
当 $ {m}^{2}=\dfrac{10-2\sqrt{7}}{5} $ 时, $ BH=\dfrac{{m}^{2}}{2}=\dfrac{5-\sqrt{7}}{5} $ ,
此时 $ O{H}^{2}=B{H}^{2}+2-2BH=\dfrac{32-10\sqrt{7}}{25}+2-2×\dfrac{5-\sqrt{7}}{5}=\dfrac{32}{25} $ ,此时 $ OH=\dfrac{4\sqrt{2}}{5} $ .
综上所述, $ OH=\dfrac{4\sqrt{2}}{5} $ .
连接 $ CH $ ,所以 $ CH\leqslant OC+OH=\sqrt{2}+\dfrac{4\sqrt{2}}{5}=\dfrac{9\sqrt{2}}{5} $ ,当且仅当 $ C $ , $ O $ , $ H $ 三点共线时,等号成立,即 $ CH $ 长度的最大值为 $ \dfrac{9\sqrt{2}}{5} $ .
由(2)可知 $ PH\perp $ 平面 $ ABCD $ ,则 $ \mathrm{\angle }PCH $ 即为直线 $ PC $ 与平面 $ ABCD $ 所成的角.
设直线 $ PC $ 与平面 $ ABCD $ 所成的角为 $ \theta $ ,显然 $ \theta \in (0,\dfrac{\mathrm{\pi }}{2}) $ ,当 $ \cos \theta $ 取最大值时, $ \theta $ 最小,此时 $ \tan \theta $ 取最小值,
所以 $ \tan \theta =\dfrac{PH}{CH}=\dfrac{\dfrac{3\sqrt{2}}{5}}{CH}\geqslant \dfrac{3\sqrt{2}}{5}×\dfrac{5}{9\sqrt{2}}=\dfrac{1}{3} $ ,
此时 $ { \cos }^{2}\theta =\dfrac{{ \cos }^{2}\theta }{{ \cos }^{2}\theta +{ \sin }^{2}\theta }=\dfrac{1}{1+{ \tan }^{2}\theta }\leqslant \dfrac{1}{1+\dfrac{1}{9}}=\dfrac{9}{10} $ ,即 $ \cos \theta $ 的最大值为 $ \dfrac{3\sqrt{10}}{10} $ ,
故当 $ 5PA\cdot PB=6\sqrt{2} $ 时,直线 $ PC $ 与平面 $ ABCD $ 所成角的余弦值的最大值为 $ \dfrac{3\sqrt{10}}{10} $ .