专题7 球的切、接问题

因为圆柱 $ {O}_{1}{O}_{2} $ 的轴截面是边长为 $ 2\sqrt{2} $ 的正方形,且圆柱 $ {O}_{1}{O}_{2} $ 上、下底面圆的圆周都在球 $ O $ 的球面上,

所以球 $ O $ 的半径 $ R=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}=\sqrt{2+2}=2 $ ,

所以球 $ O $ 的表面积是 $ 4\mathrm{\pi }×{2}^{2}=16\mathrm{\pi } $ .故选 $ \mathrm{A} $ .

设圆柱的底面半径为 $ r $ ,则其母线长 $ l=2r $ .因为圆柱的表面积公式 $ {S}_{圆柱表}=2\mathrm{\pi }{r}^{2}+2\mathrm{\pi }rl $ ,所以 $ 2\mathrm{\pi }{r}^{2}+2\mathrm{\pi }r×2r=12\mathrm{\pi } $ ,解得 $ r=\sqrt{2} $ .因为圆柱的体积公式 $ {V}_{圆柱}=Sℎ=\mathrm{\pi }{r}^{2}\cdot 2r $ ,所以 $ {V}_{圆柱}=\mathrm{\pi }×(\sqrt{2})^{2}×2\sqrt{2}=4\sqrt{2}\mathrm{\pi } $ .由题知,圆柱内切球的体积是圆柱体积的 $ \dfrac{2}{3} $ ,所以所求圆柱内切球的体积 $ V=\dfrac{2}{3}{V}_{圆柱}=\dfrac{2}{3}×4\sqrt{2}\mathrm{\pi }=\dfrac{8\sqrt{2}\mathrm{\pi }}{3} $ ,故选 $ \mathrm{D} $ .

$ \because $ 扇形的圆心角为 $ \dfrac{2\mathrm{\pi }}{3} $ ,半径为 $ {\rm 3,} \therefore $ 扇形的弧长 $ l=\dfrac{2\mathrm{\pi }}{3}×3=2\mathrm{\pi } $ ,

则该扇形所围成圆锥的底面周长为 $ 2\mathrm{\pi } $ ,底面半径 $ r=1 $ ,圆锥的高 $ ℎ=\sqrt{{3}^{2}-{1}^{2}}=2\sqrt{2} $ ,

易知圆锥外接球的球心在圆锥的高线上,如图,设球的半径为 $ R $ ,

则 $ {R}^{2}={1}^{2}+(2\sqrt{2}-R)^{2} $ ,解得 $ R=\dfrac{9\sqrt{2}}{8} $ .

$ \therefore $ 所求外接球的表面积 $ S=4\mathrm{\pi }{R}^{2}=\dfrac{81\mathrm{\pi }}{8} $ .故选 $ \mathrm{D} $ .

$ \mathrm{A} $ 选项,底面半径为3,则底面圆周长为 $ 2\mathrm{\pi }×3=6\mathrm{\pi } $ ,又母线长为4,

则侧面积为 $ \dfrac{1}{2}×6\mathrm{\pi }×4=12\mathrm{\pi } $ ,故 $ \mathrm{A} $ 正确.

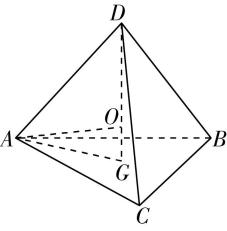
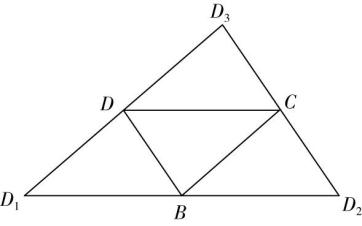
$ \mathrm{B} $ 选项,由母线长为4,底面半径为3,可得圆锥的高 $ SO=\sqrt{{4}^{2}-{3}^{2}}=\sqrt{7} $ .设 $ BC $ 是底面圆的一条直径,如图①,

则在 $ △SBC $ 中, $ \cos \mathrm{\angle }BSC=\dfrac{{4}^{2}+{4}^{2}-{6}^{2}}{2×4×4}=-\dfrac{1}{8} < 0 $ ,则 $ \mathrm{\angle }BSC $ 是钝角,

又 $ {S}_{△SPQ}=\dfrac{1}{2}\cdot SP\cdot SQ\cdot \sin \mathrm{\angle }PSQ=\dfrac{1}{2}×4×4× \sin \mathrm{\angle }PSQ=8 \sin \mathrm{\angle }PSQ $ ,

则存在点 $ P $ , $ Q $ ,当 $ \mathrm{\angle }PSQ={90}^{\circ } $ 时, $ \sin \mathrm{\angle }PSQ=1 $ , $ \therefore △SPQ $ 面积的最大值为8,故 $ \mathrm{B} $ 错误.

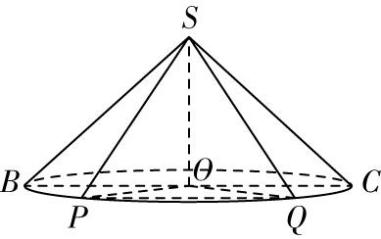
图①

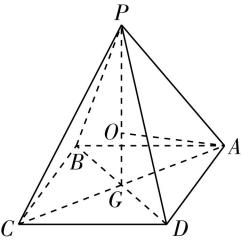
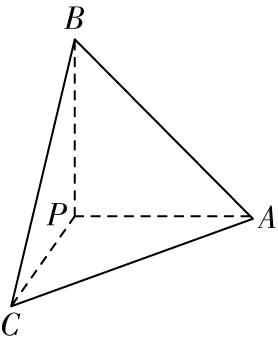
$ \mathrm{C} $ 选项, $ {S}_{△SOP}=\dfrac{1}{2}\cdot SO\cdot OP=\dfrac{1}{2}×\sqrt{7}×3=\dfrac{3\sqrt{7}}{2} $ ,由圆锥的几何特征知三棱锥 $ Q-SOP $ 的高在圆锥底面上, $ \therefore $ 当 $ OQ\perp OP $ ,即 $ OQ $ 为三棱锥 $ Q-SOP $ 的高时,

$ {({V}_{O-SPQ})}_{ \max }={({V}_{Q-SOP})}_{ \max }=\dfrac{1}{3}×{S}_{△SOP}×OQ=\dfrac{1}{3}×\dfrac{3\sqrt{7}}{2}×3=\dfrac{3\sqrt{7}}{2} $ ,故 $ \mathrm{C} $ 正确.

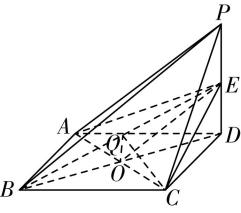
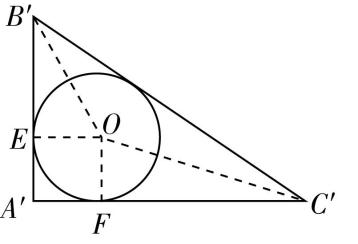
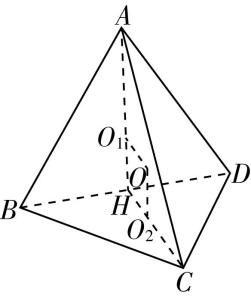
$ \mathrm{D} $ 选项,设内切球球心为 $ {O}_{1} $ ,则 $ {O}_{1} $ 在线段 $ SO $ 上,半径为 $ r $ ,过 $ {O}_{1} $ 作 $ {O}_{1}E\perp SC $ ,如图②,则 $ {O}_{1}E=O{O}_{1}=r $ , $ \mathrm{\angle }OSC=\mathrm{\angle }ES{O}_{1} $ , $ \mathrm{\angle }SOC=\mathrm{\angle }SE{O}_{1} $ ,则 $ △SOC\sim △SE{O}_{1} $ ,

则 $ \dfrac{OC}{{O}_{1}E}=\dfrac{SC}{S{O}_{1}} $ ,即 $ \dfrac{3}{r}=\dfrac{4}{\sqrt{7}-r} $ ,解得 $ r=\dfrac{3\sqrt{7}}{7} $ ,

$ \therefore $ 内切球表面积为 $ 4\mathrm{\pi }{r}^{2}=4\mathrm{\pi }×\dfrac{9}{7}=\dfrac{36\mathrm{\pi }}{7} $ , $ \mathrm{D} $ 正确.

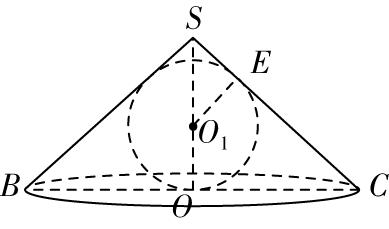
图②

故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .

不妨设 $ △ABC $ 的直角顶点为 $ A $ ，底面直角三角形的外接圆的半径为 $ r $ ,则 $ 2r=BC=\sqrt{{1}^{2}+(\sqrt{3})^{2}}=2 $ .

设直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 上、下底面直角三角形的外心（斜边的中点）分别为 $ {O}_{1} $ , $ {O}_{2} $ ,

则直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 外接球的球心为 $ {O}_{1}{O}_{2} $ 的中点 $ O $ .

又因为直三棱柱的高 $ ℎ=2\sqrt{3} $ ,所以外接球的直径为 $ 2R=B{C}_{1}=\sqrt{(2r)^{2}+{ℎ}^{2}}=\sqrt{{2}^{2}+(2\sqrt{3})^{2}}=4 $ ,即 $ R=2 $ ,

所以该三棱柱的外接球的体积为 $ \dfrac{4}{3}\mathrm{\pi }{R}^{3}=\dfrac{32}{3}\mathrm{\pi } $ .故选 $ \mathrm{A} $ .

因为直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 中, $ A{A}_{1}=1 $ , $ BC=\sqrt{3} $ , $ \mathrm{\angle }BAC={120}^{\circ } $ ,

所以 $ △ABC $ 的外接圆半径 $ r $ 满足 $ \dfrac{BC}{ \sin \mathrm{\angle }BAC}=2r $ ,即 $ \dfrac{\sqrt{3}}{ \sin {120}^{\circ }}=2r $ ,所以 $ r=1 $ ,

又直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 中,侧棱垂直于底面,所以该三棱柱外接球的球心到平面 $ ABC $ 的距离 $ d=\dfrac{A{A}_{1}}{2}=\dfrac{1}{2} $ ,

所以该三棱柱外接球的半径 $ R=\sqrt{{d}^{2}+{r}^{2}}=\sqrt{\dfrac{1}{4}+1}=\dfrac{\sqrt{5}}{2} $ ,

故所求外接球的体积 $ V=\dfrac{4}{3}\mathrm{\pi }{R}^{3}=\dfrac{4}{3}\mathrm{\pi }×\dfrac{5\sqrt{5}}{8}=\dfrac{5\sqrt{5}}{6}\mathrm{\pi } $ .故选 $ \mathrm{B} $ .

设正三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 的底面边长为 $ a $ ,侧棱长为 $ b $ ,则所有的棱长之和为 $ 6a+3b=3t $ （ $ t $ 为正实数）,所以 $ b=t-2a $ .

设正三棱柱的外接球半径为 $ R $ ,底面外接圆的半径为 $ r $ .

由正弦定理得 $ 2r=\dfrac{a}{ \sin \dfrac{\mathrm{\pi }}{3}}=\dfrac{2a}{\sqrt{3}} $ ,解得 $ r=\dfrac{a}{\sqrt{3}} $ ,所以 $ {R}^{2}={\left(\dfrac{b}{2} \right) ^ {2}}+{\left(\dfrac{a}{\sqrt{3}} \right) ^ {2}}=\dfrac{{b}^{2}}{4}+\dfrac{{a}^{2}}{3}=\dfrac{3{b}^{2}+4{a}^{2}}{12}=\dfrac{4{a}^{2}+3 (t-2a)^{2}}{12}=\dfrac{16{a}^{2}-12at+3{t}^{2}}{12} $ .当 $ a=-\dfrac{-12t}{32}=\dfrac{3t}{8} $ 时, $ {R}^{2} $ 取得最小值,为 $ \dfrac{16×\dfrac{9{t}^{2}}{64}-12t×\dfrac{3t}{8}+3{t}^{2}}{12}=\dfrac{{t}^{2}}{16} $ .

由正三棱柱外接球的表面积取得最小值 $ 16\mathrm{\pi }=4\mathrm{\pi }\cdot \dfrac{{t}^{2}}{16} $ ,解得 $ t=8 $ .

所以 $ a=\dfrac{3}{8}×8=3 $ , $ b=8-2×3=2 $ ,

所以此时正三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 的侧面积为 $ 3a\cdot b=3×3×2=18 $ ．故选 $ \mathrm{D} $ ．

因为直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 的高为2,设内切球的半径为 $ r $ ,则 $ 2r=2 $ ,所以 $ r=1 $ .若直三棱柱存在内切球,取过球心 $ O $ 的横截面如图所示,截面 $ △A^\prime B^\prime C^\prime ≌ $ 底面 $ △ABC $ ,截面圆与 $ A^\prime B^\prime $ , $ A^\prime C^\prime $ 的切点分别记为 $ E $ , $ F $ ,连接 $ OE $ , $ OF $ , $ OB\prime $ , $ OC\prime $ ,则 $ OE=OF=1 $ .设 $ \mathrm{\angle }A^\prime B^\prime C^\prime =\alpha $ , $ \mathrm{\angle }A^\prime C^\prime B^\prime =\beta $ ,则 $ \alpha +\beta =\dfrac{\mathrm{\pi }}{2} $ ,所以 $ B^\prime E=\dfrac{OE}{ \tan \dfrac{\alpha }{2}}=\dfrac{1}{ \tan \dfrac{\alpha }{2}} $ , $ C^\prime F=\dfrac{OF}{ \tan \dfrac{\beta }{2}}=\dfrac{1}{ \tan \dfrac{\beta }{2}} $ ,所以 $ △ABC $ 的周长 $ L=(\dfrac{1}{ \tan \dfrac{\alpha }{2}}+\dfrac{1}{ \tan \dfrac{\beta }{2}})\cdot 2+2 $ .

而 $ \dfrac{1}{ \tan \dfrac{\alpha }{2}}+\dfrac{1}{ \tan \dfrac{\beta }{2}}=\dfrac{ \cos \dfrac{\alpha }{2}}{ \sin \dfrac{\alpha }{2}}+\dfrac{ \cos \dfrac{\beta }{2}}{ \sin \dfrac{\beta }{2}}=\dfrac{ \sin \dfrac{\beta }{2} \cos \dfrac{\alpha }{2}+ \cos \dfrac{\beta }{2} \sin \dfrac{\alpha }{2}}{ \sin \dfrac{\alpha }{2}\cdot \sin \dfrac{\beta }{2}}=\dfrac{ \sin (\dfrac{\beta }{2}+\dfrac{\alpha }{2})}{ \sin \dfrac{\alpha }{2}\cdot \sin \dfrac{\beta }{2}}=\dfrac{\dfrac{\sqrt{2}}{2}}{-\dfrac{1}{2}[ \cos (\dfrac{\alpha }{2}+\dfrac{\beta }{2})- \cos (\dfrac{\alpha }{2}-\dfrac{\beta }{2})]}= $

$ -\dfrac{\sqrt{2}}{\dfrac{\sqrt{2}}{2}- \cos (\dfrac{\alpha }{2}-\dfrac{\beta }{2})}=\dfrac{\sqrt{2}}{ \cos (\alpha -\dfrac{\mathrm{\pi }}{4})-\dfrac{\sqrt{2}}{2}} $ ,

因为 $ \alpha \in (0,\dfrac{\mathrm{\pi }}{2}) $ ,所以 $ \cos (\alpha -\dfrac{\mathrm{\pi }}{4})\in (\dfrac{\sqrt{2}}{2},1] $ , $ \cos (\alpha -\dfrac{\mathrm{\pi }}{4})-\dfrac{\sqrt{2}}{2} > 0 $ ,则当 $ \alpha =\dfrac{\mathrm{\pi }}{4} $ 时, $ \cos (\alpha -\dfrac{\mathrm{\pi }}{4}) $ 的值最大,为1,此时 $ \dfrac{1}{ \tan \dfrac{\alpha }{2}}+\dfrac{1}{ \tan \dfrac{\beta }{2}} $ 的值最小,为 $ 2\sqrt{2}+2 $ ,所以底面 $ △ABC $ 周长的最小值为 $ 2×(2\sqrt{2}+2)+2=6+4\sqrt{2} $ .

正四棱锥 $ P-ABCD $ 的外接球的球心 $ O $ 在正四棱锥 $ P-ABCD $ 的高所在直线上,如图,连接 $ AC $ , $ BD $ 交于点 $ G $ ,连接 $ PG $ , $ OA $ .

正四棱锥的底面边长为 $ \sqrt{3} $ ,设正四棱锥的高为 $ h=PG $ ,

则正四棱锥的体积 $ V=\dfrac{1}{3}×(\sqrt{3})^{2}\cdot h=\dfrac{3\sqrt{2}}{2} $ ,解得 $ h=\dfrac{3\sqrt{2}}{2} $ ,

设球 $ O $ 的半径为 $ R $ , $ AG=\dfrac{1}{2}AC=\dfrac{1}{2}×\sqrt{3+3}=\dfrac{\sqrt{6}}{2} $ ,

则 $ {\left(\dfrac{3\sqrt{2}}{2}-R\right) ^ {2}}+{\left(\dfrac{\sqrt{6}}{2}\right) ^ {2}}={R}^{2} $ ,解得 $ R=\sqrt{2} $ ,

则球 $ O $ 的表面积 $ S={4\mathrm{\pi }R}^{2}=4\mathrm{\pi }×(\sqrt{2})^{2}=8\mathrm{\pi } $ .故选 $ \mathrm{B} $ .

如图①所示,记 $ {D}_{1}{D}_{2} $ , $ {D}_{2}{D}_{3} $ , $ {D}_{1}{D}_{3} $ 的中点分别为 $ B $ , $ C $ , $ D $ .

因为 $ {D}_{1}{D}_{2}=24 $ , $ {D}_{1}{D}_{3}=20 $ , $ {D}_{2}{D}_{3}=16 $ ,所以由中位线性质可得 $ DC=12 $ , $ BC=10 $ , $ DB=8 $ .

翻折后的四面体如图②所示,由翻折的性质可得, $ AB=12 $ , $ AD=10 $ , $ AC=8 $ ,

所以四面体 $ ABCD $ 的对棱相等,故可以考虑将四面体 $ ABCD $ 补形为长方体,如图③所示,

四面体 $ ABCD $ 的外接球即长方体的外接球.

设长方体的外接球半径为 $ R $ ,

则 $ \begin{cases}B{M}^{2}+B{N}^{2}={12}^{2},\\ B{P}^{2}+B{N}^{2}={8}^{2},\\ B{M}^{2}+B{P}^{2}={10}^{2},\end{cases} $

所以 $ B{M}^{2}+B{N}^{2}+B{P}^{2}=154 $ ,

故 $ 4{R}^{2}=B{M}^{2}+B{N}^{2}+B{P}^{2}=154 $ ,

所以四面体 $ ABCD $ 的外接球表面积 $ S=4\mathrm{\pi }{R}^{2}=154\mathrm{\pi } $ .

故选 $ \mathrm{C} $ .

图①     图②     图③

在 $ △ABC $ 中, $ \mathrm{\angle }CAB={120}^{\circ } $ , $ BC=2 $ ,

设 $ △ABC $ 的外接圆半径为 $ r $ ,

根据正弦定理,得 $ 2r=\dfrac{BC}{ \sin \mathrm{\angle }CAB}=\dfrac{2}{ \sin {120}^{\circ }}=\dfrac{4\sqrt{3}}{3} $ ,得 $ r=\dfrac{2\sqrt{3}}{3} $ .

设三棱锥外接球的半径为 $ R $ ,则 $ {R}^{2}={r}^{2}+{\left(\dfrac{SA}{2}\right) ^ {2}}=\dfrac{4}{3}+4=\dfrac{16}{3} $ ,

所以三棱锥外接球的表面积为 $ 4\mathrm{\pi }{R}^{2}=\dfrac{64\mathrm{\pi }}{3} $ .

故选 $ \mathrm{D} $ .

当三棱锥 $ A-BCD $ 的体积最大时,平面 $ ABD\perp $ 平面 $ BCD $ ,如图,取 $ BD $ 的中点为 $ H $ ,连接 $ AH $ , $ CH $ ,则 $ AH\perp BD $ .

设 $ {O}_{1} $ , $ {O}_{2} $ 分别为 $ △ABD $ , $ △BCD $ 外接圆的圆心, $ O $ 为三棱锥 $ A-BCD $ 的外接球的球心,则 $ {O}_{1} $ 在 $ AH $ 上, $ {O}_{2} $ 在 $ CH $ 上,且 $ A{O}_{1}=2{O}_{1}H=\dfrac{2}{3}AH=2\sqrt{3} $ ,且 $ {O}_{2}H\perp BD $ , $ O{O}_{1}\perp $ 平面 $ ABD $ , $ O{O}_{2}\perp $ 平面 $ BCD.\because $ 平面 $ ABD\perp $ 平面 $ BCD $ ,平面 $ ABD\cap $ 平面 $ BCD=BD $ , $ AH\subset $ 平面 $ ABD $ , $ AH\perp BD $ , $ \therefore AH\perp $ 平面 $ BCD $ , $ \therefore AH//{O}_{2}O $ ,同理 $ CH//{O}_{1}O $ , $ \therefore $ 四边形 $ {O}_{1}O{O}_{2}H $ 为平行四边形 $ {\rm .} \because AH\perp $ 平面 $ BCD $ , $ {O}_{2}H\subset $ 平面 $ BCD $ , $ \therefore AH\perp {O}_{2}H $ ,即四边形 $ {O}_{1}O{O}_{2}H $ 为矩形 $ {\rm .} \therefore O{O}_{2}={O}_{1}H=\sqrt{3} $ , $ C{O}_{2}=\dfrac{2}{3}×\dfrac{\sqrt{3}}{2}×6=2\sqrt{3} $ , $ \therefore $ 外接球半径 $ R=\sqrt{O{O}_{2}^{2}+C{O}_{2}^{2}}=\sqrt{3+12}=\sqrt{15} $ , $ \therefore $ 外接球的表面积为 $ 4\mathrm{\pi }{R}^{2}=60\mathrm{\pi } $ ,故选 $ \mathrm{A} $ .

设内切球的半径为 $ r $ ,则内切球的球心到四个面的距离均为 $ r $ .

因为三棱锥 $ P-ABC $ 三条侧棱 $ PA $ , $ PB $ , $ PC $ 两两互相垂直,且 $ PA=PB=PC=6 $ ,

所以 $ AB=AC=BC=6\sqrt{2} $ .

由 $ \dfrac{1}{3}({S}_{△ACP}+{S}_{△APB}+{S}_{△PCB}+{S}_{△ABC})r=\dfrac{1}{3}{S}_{△PCB}\cdot AP $ ,得 $ [\dfrac{1}{2}×6×6+\dfrac{1}{2}×6×6+{\left(6\sqrt{2}\right) ^ {2}}]\cdot \dfrac{1}{2}×6×6+\dfrac{\sqrt{3}}{4}×r=\dfrac{1}{2}×6×6×6 $ ,解得 $ r=3-\sqrt{3} $ .故选 $ \mathrm{B} $ .

设正四面体 $ ABCD $ 的内切球半径为 $ r $ ,则内切球的表面积为 $ 4\mathrm{\pi }{r}^{2}=\dfrac{3\mathrm{\pi }}{2} $ ,解得 $ r=\dfrac{\sqrt{6}}{4} $ .

设正四面体的棱长为 $ a $ ,则根据正四面体的内切球的结论可得 $ r=\dfrac{\sqrt{6}}{12}a $ ,即 $ \dfrac{\sqrt{6}}{4}=\dfrac{\sqrt{6}}{12}a $ ,解得 $ a=3 $ .

将正四面体 $ ABCD $ 放入正方体中,如图,即正四面体的每条棱均为正方体的面对角线,此时该正方体为能装下该正四面体的最小正方体.

设正方体的棱长为 $ t $ ,则 $ {t}^{2}+{t}^{2}={3}^{2} $ ,解得 $ t=\dfrac{3\sqrt{2}}{2} $ ,

故此正方体的体积为 $ {t}^{3}={\left(\dfrac{3\sqrt{2}}{2}\right) ^ {3}}=\dfrac{27\sqrt{2}}{4} $ .故选 $ \mathrm{C} $ .

依题意,四个小球的球心 $ A $ , $ B $ , $ C $ , $ D $ 是棱长为4的正四面体的4个顶点,

设 $ O $ 是正四面体 $ D-ABC $ 的外接球的球心, $ G $ 为正三角形 $ ABC $ 的中心,则 $ O $ 在线段 $ DG $ 上,

$ AG=\dfrac{2}{3}AB \sin {60}^{\circ }=\dfrac{4\sqrt{3}}{3} $ ,所以 $ DG=\sqrt{D{A}^{2}-A{G}^{2}}=\sqrt{{4}^{2}-{\left(\dfrac{4\sqrt{3}}{3}\right) ^ {2}}}=\dfrac{4\sqrt{6}}{3} $ ,

由 $ O{A}^{2}=A{G}^{2}+(DG-OA)^{2} $ ,得 $ OA=\sqrt{6} $ ,即正四面体 $ D-ABC $ 的外接球的半径为 $ \sqrt{6} $ ,

点 $ O $ 到实心小球球面距离的最大值为 $ \sqrt{6}+2 $ ,最小值为 $ \sqrt{6}-2 $ .

对于 $ \mathrm{D} $ ,这四个实心小球可以放入一个半径为 $ \sqrt{6}+2 $ 的大球内部, $ \mathrm{D} $ 正确；

对于 $ \mathrm{C} $ ,这四个实心小球所形成的空隙内可以放入一个半径为 $ \sqrt{6}-2 $ 的小球,

而 $ \sqrt{6}-2-\dfrac{9}{20}=\sqrt{6}-\dfrac{49}{20}=\sqrt{6}-\sqrt{6+\dfrac{1}{400}} < 0 $ ,即 $ \sqrt{6}-2 < \dfrac{9}{20} $ , $ \mathrm{C} $ 错误；

对于 $ \mathrm{A} $ ,半径为 $ \sqrt{6}-2 $ 的小球的内接正方体棱长为 $ \dfrac{2(\sqrt{6}-2)}{\sqrt{3}}=\dfrac{6\sqrt{2}-4\sqrt{3}}{3} $ ,

因此这四个实心小球所形成的空隙内可以放入一个棱长为 $ \dfrac{6\sqrt{2}-4\sqrt{3}}{3} $ 的正方体, $ \mathrm{A} $ 正确；

对于 $ \mathrm{B} $ ,令半径为 $ \sqrt{6}-2 $ 的小球的内接圆柱底面圆半径为 $ r $ ,母线长为 $ l $ ,

则 $ (\sqrt{6}-2)^{2}={r}^{2}+{\left(\dfrac{1}{2}l \right) ^ {2}}\geqslant rl $ ,当且仅当 $ l=2r $ ,即 $ r=\sqrt{3}-\sqrt{2} $ , $ l=2\sqrt{3}-2\sqrt{2} $ 时取等号,即 $ rl\leqslant 10-4\sqrt{6} $ ,

故该圆柱侧面积 $ S=2\mathrm{\pi }rl\leqslant (20-8\sqrt{6})\mathrm{\pi } $ ,

因此存在一个侧面积为 $ (20-8\sqrt{6})\mathrm{\pi } $ 的圆柱可以放进这四个实心小球所形成的空隙内, $ \mathrm{B} $ 正确.

故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .

因为正四棱锥 $ P-ABCD $ 内接于球 $ O $ ,且底面 $ ABCD $ 过球心 $ O $ ,球的半径为4,所以 $ OA=OB=OC=OD=OP=4 $ ,所以 $ AB=BC=CD=DA=PA=PB=PC=PD=4\sqrt{2} $ ,所以正四棱锥 $ P-ABCD $ 的表面积 $ S=4×\dfrac{\sqrt{3}}{4}× (4\sqrt{2})^{2}+{\left(4\sqrt{2} \right) ^ {2}}=32\sqrt{3}+32 $ ,正四棱锥 $ P-ABCD $ 的体积 $ V=\dfrac{1}{3}×(4\sqrt{2})^{2}×4=\dfrac{128}{3} $ .设正四棱锥 $ P-ABCD $ 内切球的半径为 $ r $ ,则 $ V=\dfrac{1}{3}Sr=\dfrac{1}{3}(32\sqrt{3}+32)r=\dfrac{128}{3} $ ,解得 $ r=2(\sqrt{3}-1) $ ,所以该四棱锥内切球的体积为 $ \dfrac{4}{3}\mathrm{\pi }{r}^{3}=\dfrac{4}{3}\mathrm{\pi }×[2(\sqrt{3}-1)]^{3}=\dfrac{64(3\sqrt{3}-5)\mathrm{\pi }}{3} $ .

如图,连接 $ BD $ 交 $ AC $ 于点 $ O $ ,连接 $ OE $ ,

因为平面 $ PBD\cap $ 平面 $ EAC=OE $ ,且 $ PB// $ 平面 $ EAC $ , $ PB\subset $ 平面 $ PBD $ ,所以 $ PB//OE $ ,

易知 $ O $ 为 $ BD $ 的中点,则 $ E $ 为 $ PD $ 的中点.

设四面体 $ ABCE $ 外接球的球心为 $ Q $ ,连接 $ OQ $ , $ QC $ , $ QE $ ,则 $ OQ\perp $ 平面 $ ABC $ ,

设 $ OQ=h $ ,则 $ O{Q}^{2}+O{C}^{2}=Q{C}^{2}=Q{E}^{2}(\ast ) $ .

而在直角梯形 $ ODEQ $ 中, $ Q{E}^{2}=O{D}^{2}+{\left(DE-OQ\right) ^ {2}}={\left(2\sqrt{2}\right) ^ {2}}+{\left(\sqrt{2}-h\right) ^ {2}} $ ,

代入 $ (\ast ) $ 得, $ {h}^{2}+{\left(2\sqrt{2}\right) ^ {2}}={\left(\sqrt{2}-h\right) ^ {2}}+{\left(2\sqrt{2}\right) ^ {2}} $ ,解得 $ h=\dfrac{\sqrt{2}}{2} $ ,则 $ QE=\dfrac{\sqrt{34}}{2} $ ,

故四面体 $ ABCE $ 外接球的表面积为 $ 4\mathrm{\pi }×{\left(\dfrac{\sqrt{34}}{2}\right) ^ {2}}=34\mathrm{\pi } $ .

依题意, $ AB\perp AD $ , $ AB\perp AP $ , $ AD\cap AP=A $ , $ AD $ , $ AP\subset $ 平面 $ PAD $ ,所以 $ AB\perp $ 平面 $ PAD $ ,故可将四棱锥 $ P-ABCD $ 补形为如图所示的直三棱柱 $ PAD-P^\prime BC $ .

由题知 $ \mathrm{\angle }PAD=\mathrm{\angle }P^\prime BC={60}^{\circ } $ ,不妨设 $ AD=x $ , $ AP=y $ ,外接球半径为 $ R $ ,外接球的球心为点 $ O $ , $ {O}_{1} $ , $ {O}_{2} $ 分别为 $ △ADP $ , $ △BCP\prime $ 的外心,连接 $ {O}_{1}{O}_{2} $ , $ OB $ , $ {O}_{2}B $ , $ AC $ ,则 $ O $ 为 $ {O}_{1}{O}_{2} $ 的中点， $ {O}_{1}{O}_{2}\perp $ 平面 $ PAD $ , $ O{O}_{2}=\dfrac{1}{2}AB=1 $ .

于是 $ {V}_{P-ABCD}={V}_{P-ABC}+{V}_{P-ACD}=2{V}_{P-ACD}=2{V}_{C-PAD}=2×\dfrac{1}{3}×{S}_{△PAD}×AB=\dfrac{2}{3}×\dfrac{1}{2}xy \sin {60}^{\circ }×2=\dfrac{\sqrt{3}}{3}xy=3\sqrt{3} $ ,所以 $ xy=9 $ .在 $ \mathrm{R}\mathrm{t}△OB{O}_{2} $ 中, $ {R}^{2}=O{B}^{2}=O{O}_{2}^{2}+B{O}_{2}^{2}=1+{\left(\dfrac{CP\prime }{2 \sin \mathrm{\angle }CBP\prime }\right) ^ {2}}=1+\dfrac{1}{3}CP{\prime }^{2} $ ,

在 $ △BCP\prime $ 中,由余弦定理得 $ CP{\prime }^{2}={x}^{2}+{y}^{2}-2xy \cos \mathrm{\angle }CBP\prime ={x}^{2}+{y}^{2}-xy $ ,所以 $ {R}^{2}=1+\dfrac{1}{3}({x}^{2}+{y}^{2}-xy)\geqslant 1+\dfrac{1}{3}(2xy-xy)=1+\dfrac{1}{3}xy=4 $ ,当且仅当 $ x=y=3 $ 时等号成立,所以 $ R\geqslant 2 $ ,故该四棱锥外接球表面积的最小值为 $ 4\mathrm{\pi }×{2}^{2}=16\mathrm{\pi } $ .

设 $ BC $ , $ {B}_{1}{C}_{1} $ 的中点分别为 $ {O}_{1} $ , $ {O}_{2} $ ，连接 $ A{O}_{1} $ , $ {A}_{1}{O}_{2} $ , $ {O}_{1}{O}_{2} $ ，如图所示.

显然 $ {O}_{1}{O}_{2}\perp BC $ ，因为平面 $ BC{C}_{1}{B}_{1}\perp $ 平面 $ ABC $ ，平面 $ BC{C}_{1}{B}_{1}\cap $ 平面 $ ABC=BC $ ，

所以 $ {O}_{1}{O}_{2}\perp $ 平面 $ ABC $ ，显然该三棱台外接球的球心在直线 $ {O}_{1}{O}_{2} $ 上，设球心为 $ O $ .

因为 $ AB\perp AC $ ， $ BC=6 $ ， $ {A}_{1}{B}_{1}={A}_{1}{C}_{1}=4\text{  }\sqrt{2} $ ，

所以 $ A{O}_{1}=\dfrac{1}{2}×6=3 $ , $ {A}_{1}{O}_{2}=\dfrac{1}{2}\text{  }\sqrt{{\left(4\text{  }\sqrt{2}\right) ^ {2}}+{\left(4\text{  }\sqrt{2}\right) ^ {2}}}=4 $ ，

因此 $ {O}_{1}{O}_{2}=\sqrt{A{\rm A}_{1}^{2}-{\left({A}_{1}{O}_{2}-A{O}_{1}\right) ^ {2}}}=\sqrt{50-1}=7 $ .

当 $ O $ 在线段 $ {O}_{1}{O}_{2} $ 上时，如图所示.

设 $ O{A}_{1}=r $ , $ {O}_{2}O=x $ ，由勾股定理可知

$ \begin{cases}{r}^{2}={3}^{2}+{\left(7-x\right)}^{2},\\ {r}^{2}={4}^{2}+{x}^{2}\end{cases}⇒\begin{cases}x=3,\\ r=5,\end{cases} $

所以球的体积为 $ \dfrac{4\mathrm{\pi }}{3}\cdot {5}^{3}=\dfrac{500\mathrm{\pi }}{3} $ .

当 $ O $ 不在线段 $ {O}_{1}{O}_{2} $ 上时，如图所示.

设 $ O{A}_{1}=r $ , $ {O}_{2}O=x $ ，由勾股定理可知 $ \begin{cases}{r}^{2}={3}^{2}+{\left(7+x\right)}^{2},\\ {r}^{2}={4}^{2}+{x}^{2},\end{cases} $ 解得 $ x=-3 $ ,不符合题意.故选 $ \mathrm{A} $ .

作正四棱台的轴截面如图所示，分别取 $ AB,CD $ 的中点 $ E,F $ ，连接 $ EF $ ，取 $ EF $ 的中点 $ O $ ，连接 $ OB,OC $ ，过 $ O $ 作 $ OM\bot BC $ ，过 $ B $ 作 $ BN\bot DC $ ，

由题意可知 $ AB=\dfrac { \sqrt { 3 } } { 2 } $ ， $ CD=\sqrt { 3 } $ ， $ EF=\dfrac { 9 } { 4 } $ ，

则 $ OC{^{2}}=OF{^{2}}+FC{^{2}}={\left( { \dfrac { 9 } { 8 } } \right) ^ {2}}+{\left( { \sqrt { 3 } } \right) ^ {2}}=\dfrac { 273 } { 64 } $ ， $ OB{^{2}}=OE{^{2}}+EB{^{2}}={\left( { \dfrac { 9 } { 8 } } \right) ^ {2}}+{\left( { \dfrac { \sqrt { 3 } } { 4 } } \right) ^ {2}}=\dfrac { 93 } { 64 } $ ,

$ BC{^{2}}=BN{^{2}}+NC{^{2}}={\left( { \dfrac { 9 } { 4 } } \right) ^ {2}}+{\left( { \dfrac { 3\sqrt { 3 } } { 4 } } \right) ^ {2}}=\dfrac { 108 } { 16 } $ ，

则在 $ { \rm{ △ } }OBC $ 中利用余弦定理可得， $ {\cos}\angle BOC=\dfrac { OB{^{2}}+OC{^{2}}-BC{^{2}} } { 2OB\cdot OC }=\dfrac { \dfrac { 93 } { 64 }+\dfrac { 273 } { 64 }-\dfrac { 108 } { 16 } } { 2\sqrt { \dfrac { 93 } { 64 }\times \dfrac { 273 } { 64 } } }=-\dfrac { 11 } { \sqrt { 2821 } } $ ，

则 $ \sin \angle BOC=\dfrac { 30\sqrt { 3 } } { \sqrt { 2821 } } $ ，

因 $ S{{}_{ \mathrm{ △ }OBC } }=\dfrac { 1 } { 2 }OB\cdot OC\cdot \sin \angle BOC=\dfrac { 1 } { 2 }OM\cdot BC $ ，

则 $ OM=\dfrac { OB\cdot OC\cdot \sin \angle BOC } { BC }=\dfrac { \sqrt { \dfrac { 93 } { 64 }\times \dfrac { 273 } { 64 } }\times \dfrac { 30\sqrt { 3 } } { \sqrt { 2821 } } } { \dfrac { 3\sqrt { 3 } } { 2 } }=\dfrac { 15 } { 16 } < \dfrac { 9 } { 8 }=OE $ ，

在线段 $ OF $ 上取点 $ O{{}_{ 1 } } $ ，过 $ O{{}_{ 1 } } $ 作 $ O{{}_{ 1 } }K\bot BC $ ，使得 $ O{{}_{ 1 } }K=O{{}_{ 1 } }F $ ，连接 $ O{{}_{ 1 } }C $ ，

此时 $ \mathrm{ △ }O{{}_{ 1 } }FC≌\mathrm{ △ }O{{}_{ 1 } }KC $ ，

因 $ \sin \angle BCN=\dfrac { BN } { BC }=\dfrac { 9 } { 4 }\times \dfrac { 2 } { 3\sqrt { 3 } }=\dfrac { \sqrt { 3 } } { 2 } $ ，则 $ \angle BCN=60{^{\circ }} $ ，则 $ \angle O{{}_{ 1 } }CF=30{^{\circ }} $ ，

则 $ O{{}_{ 1 } }F=FC\cdot {\tan}30{^{\circ }}=\sqrt { 3 }\times \dfrac { \sqrt { 3 } } { 3 }=1 $ ，

故球的半径最大值为 $ R=1 $ ，则球表面积的最大值为 $ 4{ \rm{ π } }R{^{2}}=4{ \rm{ π } } $ .