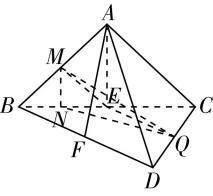
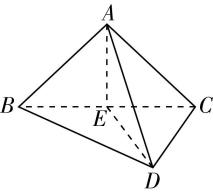
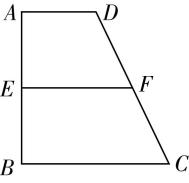
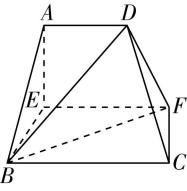
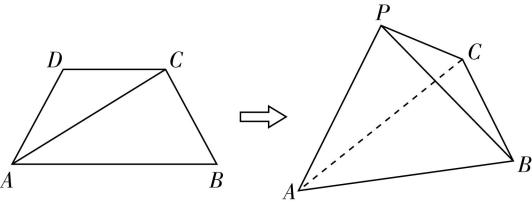
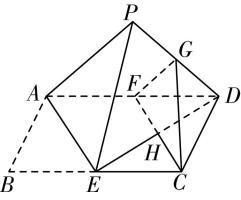
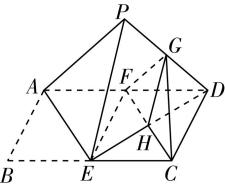
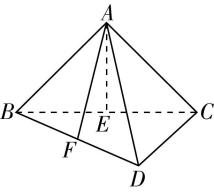
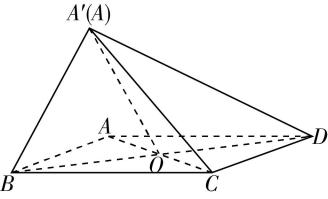
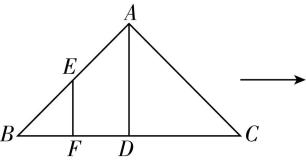
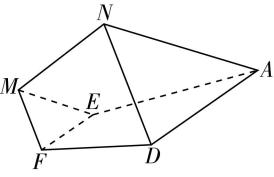
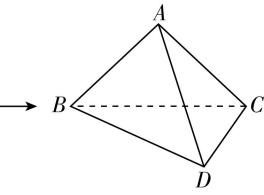
1.(多选)如图,在矩形 $ ABCD $ 中, $ E $ 为 $ BC $ 的中点, $ F $ 为 $ AD $ 的中点, $ CF $ 交 $ DE $ 于点 $ H $ ,将 $ △BAE $ 沿直线 $ AE $ 翻折到 $ △PAE $ ,连接 $ PD $ , $ G $ 为 $ PD $ 的中点,则在翻折过程中,下列结论正确的是( )
 (多选)
(多选)
A.翻折过程中,始终有平面 $ PAE// $ 平面 $ GFC $
B.翻折过程中, $ CG $ 的长是定值
C.若 $ AB=BE $ ,则 $ AE\perp ED $
D.存在某个位置,使得 $ CG\perp AP $
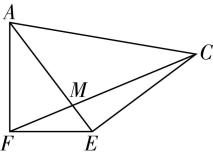
如图,连接 $ EF $ , $ GH $ .因为 $ E $ , $ F $ 分别为 $ BC $ , $ AD $ 的中点,则 $ CE//DF $ , $ CE=DF $ ,所以四边形 $ CEFD $ 是平行四边形,所以 $ H $ 是 $ ED $ 的中点.因为 $ F $ , $ G $ 分别为 $ AD $ , $ PD $ 的中点,所以 $ FG//AP $ ,
又 $ FG\not\subset $ 平面 $ PAE $ , $ AP\subset $ 平面 $ PAE $ ,所以 $ FG// $ 平面 $ PAE $ .
同理 $ GH// $ 平面 $ PAE $ .
又 $ GH\cap FG=G $ , $ GH $ , $ FG\subset $ 平面 $ GFC $ ,所以平面 $ PAE// $ 平面 $ GFC $ ,故 $ \mathrm{A} $ 正确.
由题易知 $ △PAE\sim △GFH $ ,则 $ \mathrm{\angle }GFH=\mathrm{\angle }PAE $ (定值),又 $ FG=\dfrac{1}{2}AP $ (定值), $ FC=AE $ (定值),所以在 $ △GFC $ 中,由余弦定理可知 $ CG $ 的长是定值,故 $ \mathrm{B} $ 正确.
若 $ AB=BE $ ,则 $ FA=FE=FD $ ,所以 $ \mathrm{\angle }AED={90}^{\circ } $ ,所以 $ AE\perp ED $ ,故 $ \mathrm{C} $ 正确.
因为 $ \mathrm{\angle }APE={90}^{\circ } $ ,所以 $ \mathrm{\angle }FGH={90}^{\circ } $ ,所以 $ GH\perp GF $ ,因为 $ GF $ , $ GH $ , $ GC $ 在同一平面内,所以 $ GC $ 不可能垂直于 $ GF $ ,因为 $ GF//AP $ ,所以 $ GC $ 不可能垂直于 $ AP $ ,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .


 (多选)
(多选)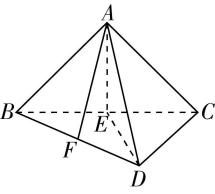


 (多选)
(多选)