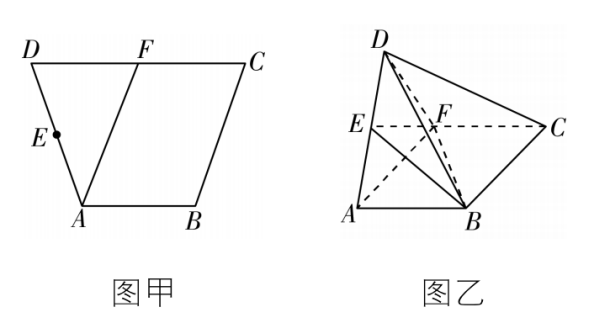
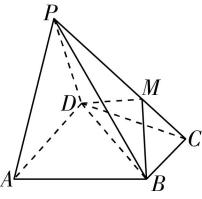
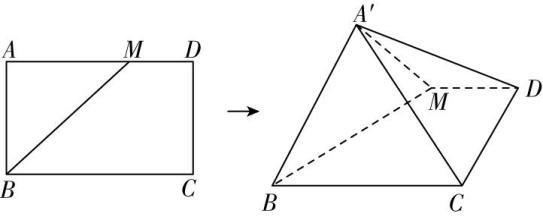
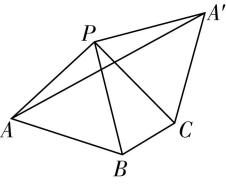
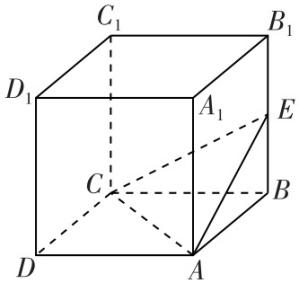
19.如图,在矩形 $ ABCD $ 中, $ AB=1 $ , $ BC=\sqrt{3} $ , $ M $ 是线段 $ AD $ 上的一动点,将 $ △ABM $ 沿着 $ BM $ 折起,使点 $ A $ 到达点 $ A^\prime $ 的位置,满足点 $ A^\prime \notin $ 平面 $ BCDM $ ,且点 $ A^\prime $ 在平面 $ BCDM $ 内的射影 $ E $ 落在线段 $ BC $ 上.
(3) 设直线 $ CD $ 与平面 $ A^\prime BM $ 所成的角为 $ \alpha $ ,二面角 $ A^\prime -BM-C $ 的平面角为 $ \beta $ ,求 $ { \sin }^{2}\alpha \cos \beta $ 的最大值.
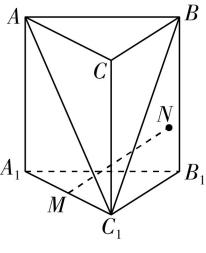
答案:(1) 【证明】如图①,当点 $ M $ 与端点 $ D $ 重合时,由 $ \mathrm{\angle }BA\prime D={90}^{\circ } $ 可知 $ A^\prime B\perp A^\prime D $ .

图①
由题意知 $ A^\prime E\perp $ 平面 $ BCD $ , $ CD\subset $ 平面 $ BCD $ ,所以 $ A^\prime E\perp CD $ .
又 $ BC\perp CD $ , $ A^\prime E\cap BC=E $ , $ A^\prime E\subset $ 平面 $ A^\prime BC $ , $ BC\subset $ 平面 $ A^\prime BC $ ,
所以 $ CD\perp $ 平面 $ A^\prime BC $ .
又 $ A^\prime B\subset $ 平面 $ A^\prime BC $ ,所以 $ A^\prime B\perp CD $ .
因为 $ A^\prime D\cap CD=D $ , $ A^\prime D\subset $ 平面 $ A^\prime CD $ , $ CD\subset $ 平面 $ A^\prime CD $ ,
所以 $ A^\prime B\perp $ 平面 $ A^\prime CD $ .
(2) 【解】如图②,过点 $ A $ 作 $ AO\perp BM $ 于点 $ O $ ,连接 $ A^\prime O $ , $ OE $ ,

图②
由题意得 $ AO\perp BM $ , $ A^\prime O\perp BM $ , $ A^\prime E\perp $ 平面 $ BCD $ ,
因为 $ BM\subset $ 平面 $ BCD $ ,所以 $ A^\prime E\perp BM $ ,
又 $ A^\prime E\cap A^\prime O=A^\prime $ , $ A^\prime E $ , $ A^\prime O\subset $ 平面 $ A^\prime OE $ ,所以 $ BM\perp $ 平面 $ A^\prime OE $ ,又 $ OE\subset $ 平面 $ A^\prime OE $ ,所以 $ BM\perp OE $ ,
所以 $ A $ , $ O $ , $ E $ 三点共线,
所以 $ \mathrm{\angle }A^\prime OE $ 为二面角 $ A^\prime -BM-C $ 的平面角.
在 $ \mathrm{R}\mathrm{t}△BAM $ 中, $ AB=1 $ , $ AM=\dfrac{3}{2} $ , $ BM=\sqrt{1+\dfrac{9}{4}}=\dfrac{\sqrt{13}}{2} $ ,由三角形面积相等可得 $ AO=\dfrac{AB\cdot AM}{BM}=\dfrac{1×\dfrac{3}{2}}{\dfrac{\sqrt{13}}{2}}=\dfrac{3\sqrt{13}}{13}=A^\prime O $ .
由题易知 $ △AOB\sim △ABE $ ,所以 $ \dfrac{AB}{AE}=\dfrac{AO}{AB} $ ,即 $ AE=\dfrac{A{B}^{2}}{AO}=\dfrac{1}{\dfrac{3\sqrt{13}}{13}}=\dfrac{\sqrt{13}}{3} $ ,所以 $ OE=AE-AO=\dfrac{\sqrt{13}}{3}-\dfrac{3\sqrt{13}}{13}=\dfrac{4\sqrt{13}}{39} $ ,
故在 $ \mathrm{R}\mathrm{t}△A^\prime EO $ 中, $ \cos \mathrm{\angle }A^\prime OE=\dfrac{OE}{A^\prime O}=\dfrac{\dfrac{4\sqrt{13}}{39}}{\dfrac{3\sqrt{13}}{13}}=\dfrac{4}{9} $ ,即二面角 $ A^\prime -BM-C $ 的余弦值为 $ \dfrac{4}{9} $ .
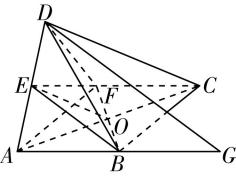
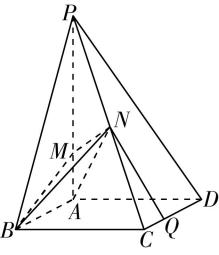
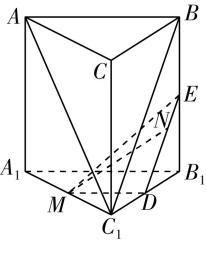
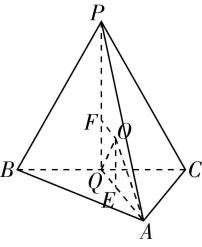
(3) 【解】如图③,过点 $ E $ 作 $ EQ//CD $ 交 $ BM $ 于 $ Q $ ,所以直线 $ EQ $ 与平面 $ A^\prime BM $ 所成的角即为直线 $ CD $ 与平面 $ A^\prime BM $ 所成的角.

图③
由(2)可知 $ BM\perp $ 平面 $ A^\prime OE $ , $ BM\subset $ 平面 $ A^\prime BM $ ,所以平面 $ A^\prime BM\perp $ 平面 $ A^\prime OE $ .
如图④,过点 $ E $ 作 $ EH\perp A^\prime O $ ,垂足为 $ H $ .

图④
因为平面 $ A^\prime BM\cap $ 平面 $ A^\prime OE=A^\prime O $ , $ EH\subset $ 平面 $ A^\prime OE $ ,所以 $ EH\perp $ 平面 $ A^\prime BM $ .
连接 $ HQ $ ,则 $ \mathrm{\angle }EQH $ 是直线 $ EQ $ 与平面 $ A^\prime BM $ 所成的角,即 $ \mathrm{\angle }EQH=\alpha $ .
由题易知 $ △ABE\sim △MAB $ ,所以 $ \dfrac{AB}{BE}=\dfrac{MA}{AB} $ .
设 $ MA=t $ , $ 0 < t\leqslant \sqrt{3} $ ,则 $ BE=\dfrac{1}{t} $ , $ BM=\sqrt{{t}^{2}+1} $ , $ OE=\dfrac{1}{t\sqrt{{t}^{2}+1}} $ , $ AO=A^\prime O=\dfrac{t}{\sqrt{{t}^{2}+1}} $ .
因为在 $ \mathrm{R}\mathrm{t}△A^\prime OE $ 中,斜边大于直角边,即 $ A^\prime O > OE $ ,
所以 $ \dfrac{t}{\sqrt{{t}^{2}+1}} > \dfrac{1}{t\sqrt{{t}^{2}+1}} $ ,所以 $ 1 < t\leqslant \sqrt{3} $ ,
$ A^\prime E=\sqrt{A^\prime {O}^{2}-O{E}^{2}}=\dfrac{\sqrt{{t}^{2}-1}}{t} $ .
在 $ △A^\prime OE $ 中, $ EH=\dfrac{A^\prime E\cdot OE}{A^\prime O}=\dfrac{\sqrt{{t}^{2}-1}}{{t}^{3}} $ , $ EQ=\dfrac{1}{{t}^{2}} $ , $ { \sin }^{2}\alpha ={\left(\dfrac{EH}{EQ}\right) ^ {2}}=1-\dfrac{1}{{t}^{2}} $ .
因为 $ A^\prime O\perp BM $ , $ OE\perp BM $ ,所以 $ \mathrm{\angle }A^\prime OE $ 是二面角 $ A^\prime -BM-C $ 的平面角,
即 $ \mathrm{\angle }A^\prime OE=\beta $ , $ \cos \beta =\dfrac{OE}{A^\prime O}=\dfrac{1}{{t}^{2}} $ .
所以 $ { \sin }^{2}\alpha \cos \beta =(1-\dfrac{1}{{t}^{2}})\cdot \dfrac{1}{{t}^{2}}=-{\left(\dfrac{1}{{t}^{2}}-\dfrac{1}{2}\right) ^ {2}}+\dfrac{1}{4}\leqslant \dfrac{1}{4} $ ,当且仅当 $ t=\sqrt{2} $ 时,等号成立.
故 $ { \sin }^{2}\alpha \cos \beta $ 的最大值为 $ \dfrac{1}{4} $ .
 (多选)
(多选)