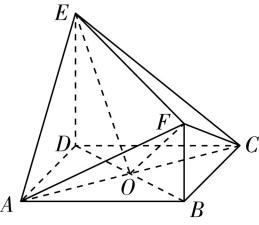
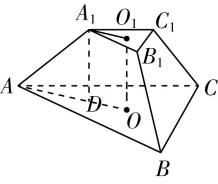
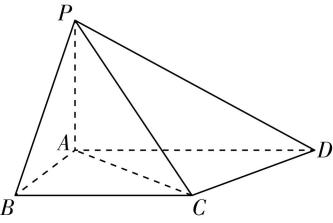
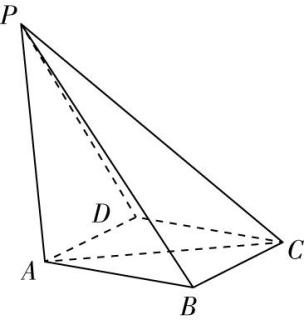
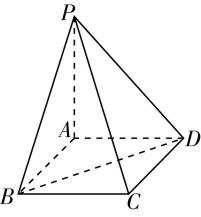
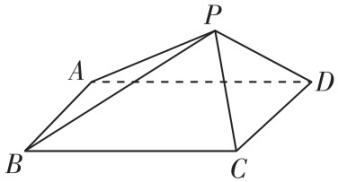
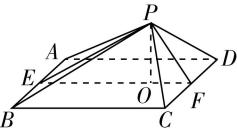
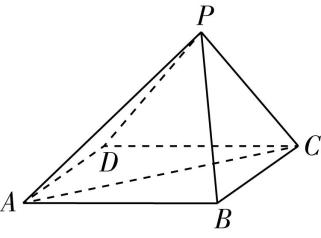
23.如图,在四棱锥 $ P-ABCD $ 中, $ PA\perp $ 底面 $ ABCD $ , $ AB\perp AD $ , $ BC//AD $ .
(2) 设 $ PA=AB=\sqrt{2} $ , $ BC=2 $ , $ AD=1+\sqrt{3} $ ,且点 $ P $ , $ B $ , $ C $ , $ D $ 均在球 $ O $ 的球面上.
(ⅱ) 求直线 $ AC $ 与 $ PO $ 所成角的余弦值.
答案:(1) 【证明】由题意知,在四棱锥 $ P-ABCD $ 中, $ PA\perp $ 平面 $ ABCD $ , $ AB\perp AD $ , $ AB\subset $ 平面 $ ABCD $ , $ AD\subset $ 平面 $ ABCD $ ,
$ \therefore AP\perp AB $ , $ AP\perp AD $ .
$ \because AP\subset $ 平面 $ PAD $ , $ AD\subset $ 平面 $ PAD $ , $ AP\cap AD=A $ ,
$ \therefore AB\perp $ 平面 $ PAD $ .
$ \because AB\subset $ 平面 $ PAB $ ,
$ \therefore $ 平面 $ PAB\perp $ 平面 $ PAD $ .
(2) (ⅰ) 【证明】 $ \because P $ , $ B $ , $ C $ , $ D $ 在同一个球面上,
$ \therefore $ 球心到四个点的距离相等.
在 $ △BCD $ 中,到三角形三个顶点距离相等的点是该三角形的外心,
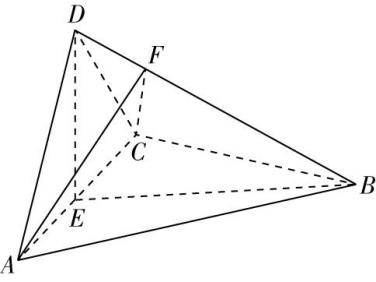
作出 $ BC $ 的垂直平分线,交 $ AD $ 于 $ {O}_{1} $ ,连接 $ B{O}_{1} $ , $ C{O}_{1} $ ,如图所示,

由图可知 $ {O}_{1}E=AB=\sqrt{2} $ , $ BE=CE=A{O}_{1}=\dfrac{1}{2}BC=1 $ , $ {O}_{1}D=AD-A{O}_{1}=\sqrt{3} $ ,
$ B{O}_{1}=C{O}_{1}=\sqrt{{1}^{2}+(\sqrt{2})^{2}}=\sqrt{3} $ ,
$ \therefore {O}_{1}D=B{O}_{1}=C{O}_{1} $ ,
$ \therefore $ 点 $ {O}_{1} $ 是 $ △BCD $ 的外心,
在 $ \mathrm{R}\mathrm{t}△A{O}_{1}P $ 中, $ AP\perp AD $ , $ AP=\sqrt{2} $ ,
由勾股定理得, $ P{O}_{1}=\sqrt{A{P}^{2}+A{O}_{1}^{2}}=\sqrt{(\sqrt{2})^{2}+{1}^{2}}=\sqrt{3} $ ,
$ \therefore P{O}_{1}=B{O}_{1}=C{O}_{1}={O}_{1}D=\sqrt{3} $ ,
$ \therefore $ 点 $ {O}_{1} $ 即为点 $ P $ , $ B $ , $ C $ , $ D $ 所在球的球心 $ O $ ,
此时点 $ O $ 在线段 $ AD $ 上, $ AD\subset $ 平面 $ ABCD $ ,
$ \therefore $ 点 $ O $ 在平面 $ ABCD $ 内.
(ⅱ) 【解】由(ⅰ)可知, $ PO=\sqrt{3} $ ,
$ \because AB\perp AD $ , $ BC//AD $ ,
$ \therefore AB\perp BC $ ,
在 $ \mathrm{R}\mathrm{t}△ABC $ 中, $ AB=\sqrt{2} $ , $ BC=2 $ ,由勾股定理得 $ AC=\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{(\sqrt{2})^{2}+{2}^{2}}=\sqrt{6} $ ,
过点 $ O $ 作 $ AC $ 的平行线,交 $ BC $ 的延长线于 $ {C}_{1} $ ,连接 $ A{C}_{1} $ , $ P{C}_{1} $ ,如图所示,

$ \because AD//BC $ , $ \therefore $ 四边形 $ AO{C}_{1}C $ 为平行四边形, $ \therefore O{C}_{1}=AC=\sqrt{6} $ ,直线 $ AC $ 与直线 $ PO $ 所成角为 $ \mathrm{\angle }PO{C}_{1} $ 或其补角.
$ \because PA\perp $ 平面 $ ABCD $ , $ A{C}_{1}\subset $ 平面 $ ABCD $ ,
$ \therefore PA\perp A{C}_{1} $ ,
在 $ \mathrm{R}\mathrm{t}△AB{C}_{1} $ 中, $ AB=\sqrt{2} $ , $ B{C}_{1}=BC+C{C}_{1}=2+1=3 $ ,由勾股定理得 $ A{C}_{1}=\sqrt{A{B}^{2}+B{\rm C}_{1}^{2}}=\sqrt{(\sqrt{2})^{2}+{3}^{2}}=\sqrt{11} $ ,
在 $ \mathrm{R}\mathrm{t}△AP{C}_{1} $ 中, $ PA=\sqrt{2} $ ,由勾股定理得 $ P{C}_{1}=\sqrt{P{A}^{2}+A{\rm C}_{1}^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{11})^{2}}=\sqrt{13} $ ,
在 $ △PO{C}_{1} $ 中,由余弦定理得 $ P{\rm C}_{1}^{2}=P{O}^{2}+O{\rm C}_{1}^{2}-2PO\cdot O{C}_{1} \cos \mathrm{\angle }PO{C}_{1} $ ,
即 $ (\sqrt{13})^{2}=(\sqrt{3})^{2}+(\sqrt{6})^{2}-2×\sqrt{3}×\sqrt{6}\cdot \cos \mathrm{\angle }PO{C}_{1} $ ,解得 $ \cos \mathrm{\angle }PO{C}_{1}=-\dfrac{\sqrt{2}}{3} $ .
$ \therefore $ 直线 $ AC $ 与直线 $ PO $ 所成角的余弦值为 $ \cos (\mathrm{\pi }-\mathrm{\angle }PO{C}_{1})=\dfrac{\sqrt{2}}{3} $ .
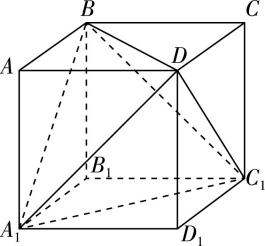
 (多选)
(多选)