1．关于频率分布表,下列叙述中正确的是（ ）
A．从频率分布表可以看出样本数据相对于平均数的波动大小
B．频数是指落在各个小组内的数据
C．每个小组的频数与样本容量之比是这个小组的频率
D．组数是样本平均数除以组距
对于 $ \mathrm{A} $ 选项,频率分布表使样本数据被妥善整理,从而以更简洁的数据形态呈现,无法通过频率分布表看出数据相对于平均数的波动情况, $ \mathrm{A} $ 错误;对于 $ \mathrm{B} $ 选项,频数是指落在各个小组内的数据的个数, $ \mathrm{B} $ 错误;对于 $ \mathrm{C} $ 选项,每个小组的频数与样本容量之比等于这个小组的频率, $ \mathrm{C} $ 正确;对于 $ \mathrm{D} $ 选项,组数一般由样本数据的极差除以组距得到, $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
2．一个样本容量为600的频数分布表不小心被损坏了一部分.若样本中数据在 $ [0.2,0.8) $ 内的频率为 $ 0.75 $ ，则样本中数据在 $ [0.4,0.8) $ 内的个数为（ ）
A．225
B．295
C．235
D．305
因为数据在 $ [0.2,0.8) $ 内的频率为 $ 0.75 $ ,所以数据在 $ [0.2,0.8) $ 内的频数为 $ 600×0.75=450 $ ,故样本中数据在 $ [0.4,0.8) $ 内的个数为 $ 450-95-120=235 $ .故选 $ \mathrm{C} $ .
3．为进一步在社会上普及垃圾分类知识，某中学学生积极到社会上举行垃圾分类的公益讲座，该校学生会为了解本校高一年级1 000名学生课余时间参加该公益讲座的情况，随机抽取50名学生进行调查，将数据分组整理后，列表如下：
参加场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
参加人数占调查人数的百分比 | $ 8\% $ | $ 10\% $ | $ 20\% $ | $ 26\% $ | $ 18\% $ | $ 12\% $ | $ 4\% $ | $ 2\% $ |
下列估计该校高一年级学生参加公益讲座的情况正确的是 .
（1）参加公益讲座3场的学生约有360人；
（2）参加公益讲座2场和4场的学生约有480人；
（3）参加公益讲座不高于2场的学生约有280人；
（4）参加公益讲座不低于4场的学生约有360人.
（4）
估计该校高一年级参加公益讲座3场的学生约有 $ 1000×0.26=260 $ 人,故（1）错误；参加公益讲座2场和4场的学生约有 $ 1000×(0.2+0.18)=380 $ 人,故（2）错误；参加公益讲座不高于2场的学生约有 $ 1000×(0.2+0.1+0.08)=380 $ 人,故（3）错误；参加公益讲座不低于4场的学生约有 $ 1000×(0.18+0.12+0.04+0.02)=360 $ 人,故（4）正确.
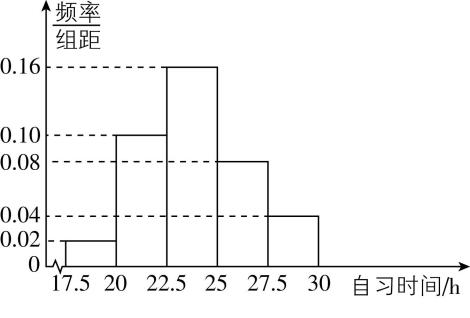
4．某高校调查了200名学生每周的自习时间（单位： $ \mathrm{h} $ ），制成了如图所示的频率分布直方图，其中自习时间的范围是 $ [17.5,30] $ ，样本数据分组为 $ [17.5,20),[20,22.5) $ ， $ [22.5,25) $ ， $ [25,27.5) $ ， $ [27.5,30] $ .根据直方图，这200名学生中每周的自习时间不少于 $ 22.5\mathrm{h} $ 的人数是（ ）
A．56
B．60
C．120
D．140
由频率分布直方图中的数据可得每周的自习时间不少于 $ 22.5\mathrm{h} $ 的频率为 $ (0.16+0.08+0.04)×2.5=0.7 $ ,则200名学生中每周的自习时间不少于 $ 22.5\mathrm{h} $ 的人数是 $ 200×0.7=140 $ .故选 $ \mathrm{D} $ .
5．为了解人们对环保知识的认知情况，某调查机构在 $ A $ 地区随机选取 $ n $ 个人进行了环保知识问卷调查（满分为100分），并根据问卷成绩（不低于60分记为及格）绘制成如图所示的频率分布直方图(分为 $ [40,50),[50,60) $ ， $ [60,70),[70,80) $ ， $ [80,90) $ ， $ [90,100] $ 六组)，若问卷成绩最后三组频数之和为360，则下列结论正确的是 .
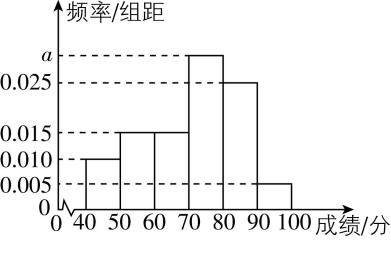
① $ n=480 $ ；
②问卷成绩在 $ [70,80) $ 内的频率为0.3；
③ $ a=0.030 $ ；
④以样本估计总体，若对 $ A $ 地区5 000人进行问卷调查，则约有1 250人不及格.
②③④
由 $ (0.010+0.015+0.015+a+0.025+0.005)×10=1 $ ,得 $ a=0.030 $ ,故 $ n=\dfrac{360}{10(a+0.025+0.005)}=600 $ ,①错误,③正确；成绩在 $ [70,80) $ 内的频率为 $ 10a=0.3 $ ,②正确.若对 $ A $ 地区5 000人进行问卷调查,则约有 $ 5000×(0.1+0.15)=1250 $ 人不及格,④正确.
6．某车站在春运期间为了了解旅客购票情况，随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间 $ t $ （以下简称为购票用时，单位： $ \min $ ），下面是这次调查统计分析得到的频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
$ 0\leqslant t < 5 $ | 0 | 0 |
$ 5\leqslant t < 10 $ | 10 | 0.10 |
$ 10\leqslant t < 15 $ | 10 | ② |
$ 15\leqslant t < 20 $ | ① | 0.50 |
$ 20\leqslant t\leqslant 25 $ | 30 | 0.30 |
合计 | 100 | 1.00 |
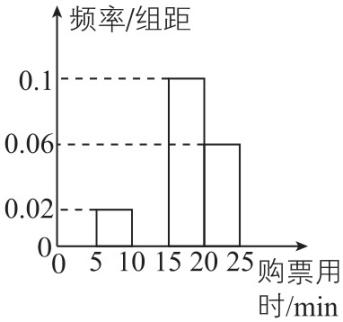
解答下列问题：
（1） 这次抽样的样本量是多少？
（2） 在表中填写出缺失的数据并补全频率分布直方图.
（3） 旅客购票用时的平均数可能落在哪一组？
（1） 【解】样本量是100.
（2） ① 50② 0.10；所补频率分布直方图如图中的阴影部分所示．
（3） 设旅客平均购票用时为 $ \overline{t} \min $ ,则有
$ \dfrac{0×0+5×10+10×10+15×50+20×30}{100}\leqslant $
$ \overline{t} < \dfrac{5×0+10×10+15×10+20×50+25×30}{100} $ ,
即 $ 15\leqslant \overline{t} < 20 $ .
所以旅客购票用时的平均数可能落在第四组中．
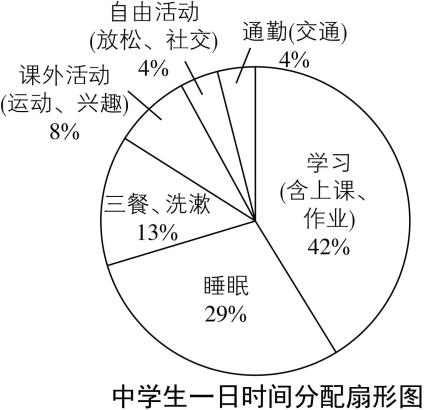
7．（多选）如图所示，下列说法正确的有（ ）
（多选）
A．该扇形图为某一位中学生的一日时间分配情况
B．该扇形图为中学生这个群体的平均一日时间分配情况
C．该图表明中学生一日睡眠时间约为 $ 7\mathrm{h} $
D．该图表明中学生一天花费在课外活动的时间与自由活动时间、通勤时间的总和相当
根据题意,题图为中学生一日时间分配扇形图,不能确定是某一位中学生的具体一日时间分配,故 $ \mathrm{A} $ 错误；
该扇形图为中学生这个群体的平均一日时间分配情况, $ \mathrm{B} $ 正确；
题图表明中学生一日睡眠时间约为 $ 24×0.29=6.96\mathrm{h} $ ,从而估计中学生一日睡眠时间为 $ 7\mathrm{h} $ , $ \mathrm{C} $ 正确；
题图表明中学生一天花费在课外活动时间的比例为 $ 8\% $ ,自由活动时间、通勤时间总的比例为 $ 8\% $ ,故中学生一天花费在课外活动的时间与自由活动时间、通勤时间的总和相当, $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
8．为了研究甲、乙两个旅游景点的游客情况，文旅局统计了2024年4月到9月甲、乙两个旅游景点的游客人数（单位：万人），得到如图所示的折线图.根据两个景点的游客人数的折线图，下列说法错误的是（ ）
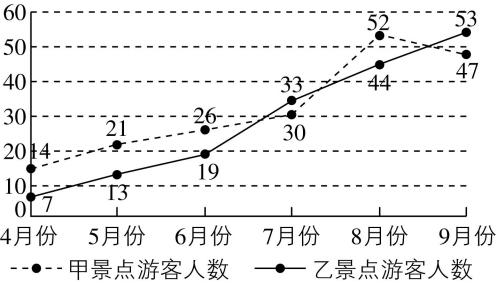
A．甲景点7，8，9月份的总游客人数比乙景点少
B．乙景点4月到9月的游客人数总体呈上升趋势
C．甲景点4月到9月游客人数的平均值在 $ [31,32] $ 内
D．甲、乙两景点4月到9月游客量的最高峰期都在8月
对于 $ \mathrm{A} $ ,由游客人数折线图可知,甲景点7,8,9月份的总游客人数为 $ 30+52+47=129 $ ,乙景点7,8,9月份的总游客人数为 $ 33+44+53=130 $ , $ 129 < 130 $ , $ \mathrm{A} $ 正确；对于 $ \mathrm{B} $ ,根据乙景点的游客人数折线图可知,乙景点的游客人数逐月增多,所以总体呈上升趋势, $ \mathrm{B} $ 正确；对于 $ \mathrm{C} $ ,甲景点游客人数的平均值为 $ \dfrac{1}{6}×(14+21+26+30+52+47)\approx 31.7 $ , $ 31.7\in [31,32] $ , $ \mathrm{C} $ 正确；对于 $ \mathrm{D} $ ,由游客人数折线图可知,甲景点4月到9月游客量的最高峰期在8月,乙景点4月到9月游客量的最高峰期在9月, $ \mathrm{D} $ 错误.故选 $ \mathrm{D} $ .
9．要调查某地区高中学生身体素质，从高中生中抽取100人进行跳远测试，根据测试成绩制作出如图所示的频率分布直方图，现再从这100人中用比例分配的分层随机抽样方法抽取20人，应从 $ [120,130) $ 中抽取的人数为 $ b $ ，则 $ b= $ （ ）
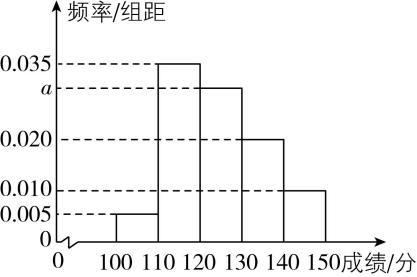
A．4
B．5
C．6
D．7
由题意得, $ 10×(0.005+0.035+a+0.020+0.010)=1 $ ,解得 $ a=0.030 $ .
样本中成绩在 $ [120,130) $ 之间的学生人数为 $ 100×10×0.030=30 $ ,
现再从这100人中用比例分配的分层随机抽样方法抽取20人,
应从 $ [120,130) $ 中抽取的人数为 $ \dfrac{30}{100}×20=6 $ ,故 $ b=6 $ .故选 $ \mathrm{C} $ .
1．某厂对一批产品进行抽样检测，如图所示的是抽检产品净重（单位:克）的频率分布直方图，样本数据分组为 $ [76,78) $ , $ [78,80) $ , $ \cdots $ , $ [84,86] $ .若这批产品有200个，估计其中净重大于或等于80克的个数是（ ）
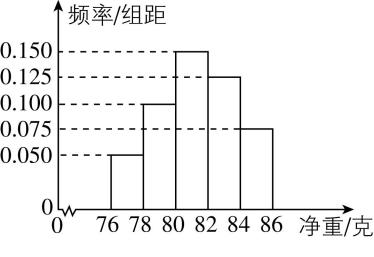
A．110
B．140
C．150
D．90
由频率分布直方图,可得产品净重大于或等于80克的频率为 $ P=(0.15+0.125+0.075)×2=0.7 $ ,所以净重大于或等于80克的个数约为 $ 200×0.7=140 $ .
故选 $ \mathrm{B} $ .
2．某年1月25日至2月12日某旅游景区 $ A $ 及其里面的特色景点 $ a $ 累计参观人次（单位：万次）的折线图如图所示，则下列判断正确的是（ ）
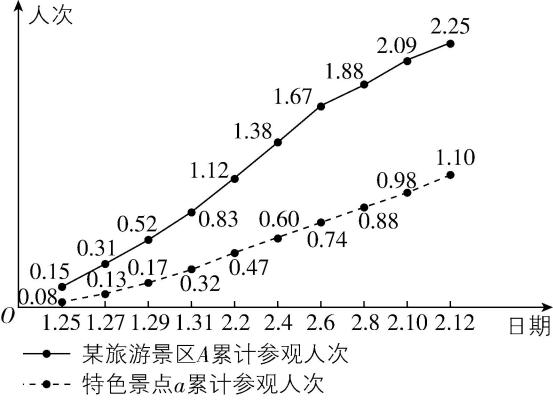
A．1月29日景区 $ A $ 累计参观人次中特色景点 $ a $ 占比超过了 $ \dfrac{1}{3} $
B．2月4日至2月10日特色景点 $ a $ 累计参观人次增加了9 800
C．2月4日至2月6日特色景点 $ a $ 的累计参观人次的增长率和2月6日至2月8日特色景点 $ a $ 累计参观人次的增长率相等
D．2月8日至2月10日景区 $ A $ 累计参观人次的增长率小于2月6日至2月8日的增长率
1月29日景区 $ A $ 累计参观人次中特色景点 $ a $ 的占比为 $ \dfrac{0.17}{0.52} < \dfrac{17}{51}=\dfrac{1}{3} $ ,故 $ \mathrm{A} $ 错误；
2月4日至2月10日特色景点 $ a $ 累计参观人次增加了 $ 9800-6000=3800 $ ,故 $ \mathrm{B} $ 错误；
2月4日至2月6日特色景点 $ a $ 累计参观人次的增长率为 $ \dfrac{0.74-0.60}{0.60}=\dfrac{7}{30} $ ,
2月6日至2月8日特色景点 $ a $ 累计参观人次的增长率为 $ \dfrac{0.88-0.74}{0.74}=\dfrac{7}{37} $ ,
因为 $ \dfrac{7}{30} > \dfrac{7}{37} $ ,所以 $ \mathrm{C} $ 错误；
2月8日至2月10日景区 $ A $ 累计参观人次的增长率为 $ \dfrac{2.09-1.88}{1.88}=\dfrac{21}{188} $ ,
2月6日至2月8日景区 $ A $ 累计参观人次的增长率为 $ \dfrac{1.88-1.67}{1.67}=\dfrac{21}{167} $ ,
因为 $ \dfrac{21}{188} < \dfrac{21}{167} $ ,所以 $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
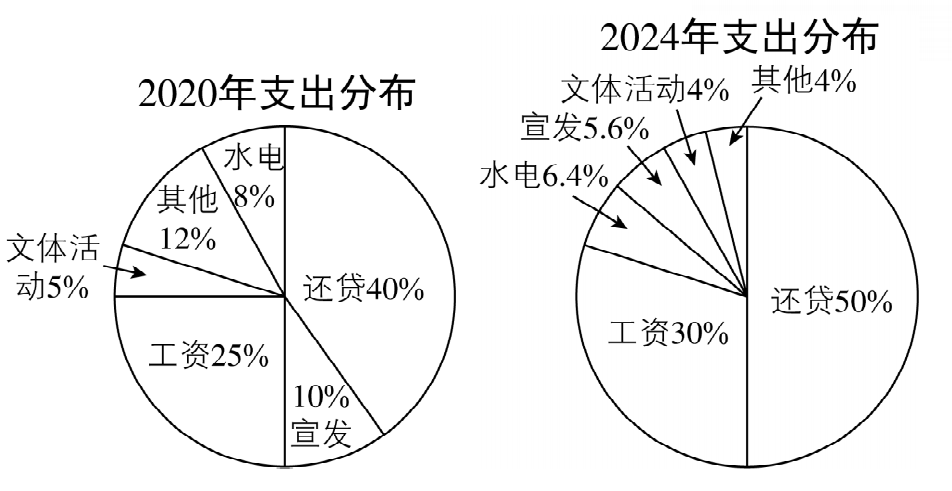
3．（多选）如图是某公司2020年和2024年支出的比例分配图，其中这两年用于文体活动的支出费用相等，则（ ）
（多选）
A．2024年总支出比2020年增长25%
B．用于宣发的支出2024年比2020年多
C．用于水电的支出2024年与2020年相等
D．用于工资的支出2024年比2020年增长 $ 50\% $
因为这两年用于文体活动的支出费用相等,设用于文体活动的支出费用均为 $ a $ ,故2020年的总支出为 $ 20a {\rm ,2024} $ 年的总支出为 $ 25a $ ,
所以2024年总支出比2020年增长 $ 25\% $ ,故 $ \mathrm{A} $ 正确；
用于宣发的支出2024年为 $ 25a×5.6\%=1.4a {\rm ,2020} $ 年为 $ 20a×10\%=2a $ ,
故用于宣发的支出2024年比2020年少,故 $ \mathrm{B} $ 错误；
用于水电的支出2024年为 $ 25a×6.4\%=1.6a {\rm ,2020} $ 年为 $ 20a×8\%=1.6a $ ,
故用于水电的支出2024年与2020年相等,故 $ \mathrm{C} $ 正确；
用于工资的支出2024年为 $ 25a×30\%=7.5a $ , $ 2020 $ 年为 $ 20a×25\%=5a $ ,
所以用于工资的支出2024年比2020年增长 $ 50\% $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
4．为庆祝中国共产党建党100周年，某校开展了以“学习百年党史，汇聚团结伟力”为主题的知识竞赛，竞赛结束后随机抽取了部分学生成绩进行统计，按成绩分成 $ A $ ， $ B $ ， $ C $ ， $ D $ ， $ E $ 五个等级，等级划分规则如表所示，并绘制了如图不完整的统计图.
等级 | 成绩 $ x $ |
$ A $ | $ 50\leqslant x < 60 $ |
$ B $ | $ 60\leqslant x < 70 $ |
$ C $ | $ 70\leqslant x < 80 $ |
$ D $ | $ 80\leqslant x < 90 $ |
$ E $ | $ 90\leqslant x\leqslant 100 $ |
请结合统计图表，解答下列问题：
（1） 本次调查一共随机抽取了 名学生的成绩，频数分布直方图中 $ m= $ ；
（2） 补全学生成绩频数分布直方图；
（3） 若成绩在80分及以上为优秀，全校共有2 000名学生，估计成绩优秀的学生有 人.
（1） 200；16
（2） 【解】由（1）知等级 $ C $ 的人数为 $ 200×25\%=50 $ ,补图如图所示.
（3） 940
（1） 根据扇形统计图及频数分布直方图可知 $ B $ 等级有40人,占总人数的 $ 20\% $ ,则抽取的总人数为 $ \dfrac{40}{20{\%}}=200 $ ,则 $ m=200×8\%=16 $ .
（3） 由扇形统计图可知成绩在80分及以上的 $ D $ , $ E $ 等级占比为 $ 1-(25\%+20\%+8\%)=47\% $ ,
所以成绩优秀的学生人数估计为 $ 47\%×2000=940 $ .