1．已知100个数据的第25百分位数是 $ 12.5 $ ，则下列说法正确的是（ ）
A．这100个数据中一定有25个数小于12.5
B．把这100个数据从小到大排列后， $ 12.5 $ 是第25个数据
C．把这100个数据从小到大排列后， $ 12.5 $ 是第24个数据和第25个数据的平均数
D．把这100个数据从小到大排列后， $ 12.5 $ 是第25个数据和第26个数据的平均数
因为 $ 100×25\%=25 $ 为整数,所以根据百分位数的定义,可知将这100个数据从小到大排列后,12.5是第25个数据和第26个数据的平均数, $ \mathrm{D} $ 正确；若这100个数均为 $ 12.5 $ ,则 $ \mathrm{A} $ , $ \mathrm{B} $ , $ \mathrm{C} $ 错误.故选 $ \mathrm{D} $ .
2．样本数据91，80，86，88，100，93，86，95的第一四分位数为（ ）
A．87
B．86
C．94
D．93
样本数据由小到大排列：80,86,86,88,91,93,95,100,
由 $ 25\%×8=2 $ ,得第一四分位数为 $ \dfrac{86+86}{2}=86 $ .故选 $ \mathrm{B} $ .
3．将10个数据按照从小到大的顺序排列如下： $ {\rm 11,15,17,} a {\rm ,23,26,27,34,37,38} $ ，若该组数据的 $ 40\% $ 分位数为22，则 $ a= $ （ ）
A．19
B．20
C．21
D．22
$ 40\%×10=4 $ ,又该组数据的 $ 40\% $ 分位数为22,则 $ \dfrac{a+23}{2}=22 $ ,解得 $ a= {\rm 21} $ .故选 $ \mathrm{C} $ .
4．设一组数据的样本量为60，经过数据整理，得出了如下所示的频数分布表，则该样本的第75百分位数为（ ）
数据分组区间 | $ [0,12) $ | $ [12,24) $ | $ [24,36) $ | $ [36,48) $ | $ [48,60] $ |
频数 | 16 | 20 | 12 | 6 | 6 |
A．31
B．32
C．33
D．34
因为 $ 60×0.75=45 $ , $ 16+20=36 $ , $ 16+20+12=48 $ ,所以第75百分位数必在 $ [24,36) $ 内.设第75百分位数为 $ x $ ,则有 $ \dfrac{x-24}{36-24}=\dfrac{45-36}{12} $ ,解得 $ x=33 $ .故选 $ \mathrm{C} $ .
5．某家水果店的店长为了解本店苹果的日销售情况，记录了近期连续120天苹果的日销售量 $ ( $ 单位: $ \mathrm{k}\mathrm{g}) $ ，并绘制频率分布直方图如图所示.一次进货太多，水果会变得不新鲜；进货太少，又不能满足顾客的需求.店长希望每天的苹果尽量新鲜，又能 $ 80\% $ 地满足顾客的需求（在10天中，大约有8天可以满足顾客的需求）.求每天应该进的苹果质量.（精确到整数位）
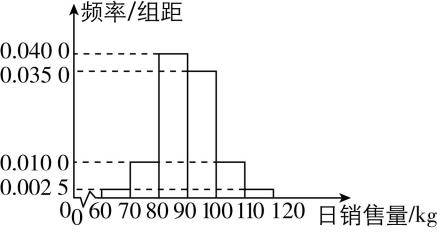
【解】 $ 80\% $ 地满足顾客的需求也可理解为计算这组数据的第80百分位数,因为日销售量 $ [60,90) $ 的频率为 $ (0.0025+0.0100+0.0400)×10=0.525 < 0.8 $ ,日销售量 $ [60,100) $ 的频率为 $ 0.525+0.0350×10=0.875 > 0.8 $ ,所以第80百分位数落在 $ [90,100) $ 内,则每天应进 $ 90+10×\dfrac{0.8-0.525}{0.875-0.525}\approx 98(\mathrm{k}\mathrm{g}) $ 苹果.
6．文明城市是反映城市整体文明水平的综合性荣誉称号，作为普通市民，既是文明城市的最大受益者，更是文明城市的主要创造者.某市为提高市民对文明城市创建的认识，举办了“创建文明城市”知识竞赛，从所有答卷中随机抽取100份作为样本，将样本的成绩（满分100分，成绩均为不低于40分的整数）分成六段： $ [40,50),[50,60) $ ， $ [60,70),[70,80) $ ， $ [80,90) $ ， $ [90,100] $ ，得到如图所示的频率分布直方图.则频率分布直方图中 $ a $ 的值为 ；样本成绩的第75百分位数为 .
0.030； 84
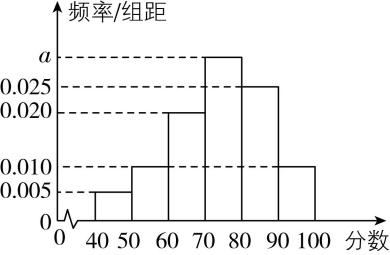
$ \because $ 每组小矩形的面积之和为1,
$ \therefore (0.005+0.010+0.020+a+0.025+0.010)×10=1 $ , $ \therefore a=0.030 $ .
成绩落在 $ [40,80) $ 内的频率为 $ (0.005+0.010+0.020+0.030)×10=0.65 < 0.75 $ ,落在 $ [40,90) $ 内的频率为 $ (0.005+0.010+0.020+0.030+0.025)×10=0.9 > 0.75 $ ， $ \therefore $ 第75百分位数落在 $ [80,90) $ 内.
设第75百分位数为 $ m $ ,由 $ 0.65+(m-80)×0.025=0.75 $ ,解得 $ m=84 $ ,故第75百分位数为84.
1．有一组数据按从小到大排序如下：70，71，73，75，76，则这组数据的 $ 50\% $ 分位数， $ 70\% $ 分位数分别是（ ）
A．71，74
B．73，74
C．73，75
D．72，75
因为 $ 5×0.5=2.5 $ , $ 5×0.7=3.5 $ ,所以这组数据的 $ 50\% $ 分位数、 $ 70\% $ 分位数分别是73,75.故选 $ \mathrm{C} $ .
3．某地区为了解最近11天该地区的空气质量，调查了该地区过去11天 $ \mathrm{P}\mathrm{M}2.5 $ 的浓度 $ ( $ 单位： $ \mu \mathrm{g}/{\mathrm{m}}^{3}) $ ，数据依次为 $ {\rm 53，56，69，70，72，79，65，80，45，41，} m(m > 50) $ .已知这组数据的极差为40，则这组数据的第 $ m $ 百分位数为（ ）
A．71
B．75.5
C．79
D．72
因为这组数据的极差为40,数据中最小值为41,所以 $ m $ 应为最大值81,则 $ 81\%×11=8.91 $ .将数据从小到大排列为 $ {\rm 41,45,} 53 {\rm ,56,65,69,70,72,79} $ , $ 80 $ , $ 81 $ ,第9个数据为79,故这组数据的第 $ m $ 百分位数为79,故选 $ \mathrm{C} $ .
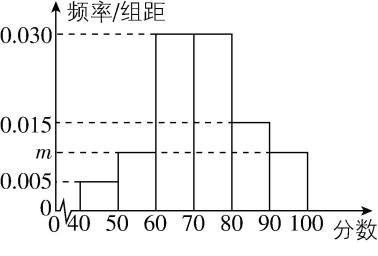
4．（多选）我国载人航天技术飞速发展，神舟二十号于2025年4月24日发射成功.某学校举行了一次航天知识竞赛活动，有100名学生参加学校决赛，把他们的成绩（均为整数）分成六组得到如图所示的频率分布直方图.则下面结论正确的是（ ）
（多选）
A．直方图中 $ m $ 的值为0.010
B．在参加学校决赛的100名学生中，成绩落在区间 $ [60,80) $ 内的有60人
C．如果规定90分以上学生获得一等奖，估计有 $ 15\% $ 的学生获得一等奖
D．根据此频率分布直方图可计算出这100名学生成绩的上四分位数为80分
对于 $ \mathrm{A} $ ,由频率分布直方图可得 $ (0.005+m+0.03+0.03+0.015+m)×10=1 $ ,解得 $ m=0.01 $ ,故 $ \mathrm{A} $ 正确；
对于 $ \mathrm{B} $ ,成绩在 $ [60,80) $ 内的人数为 $ 2×0.3×100=60 $ ,故 $ \mathrm{B} $ 正确；
对于 $ \mathrm{C} {\rm ,90} $ 分以上的频率为 $ 0.01×10=0.1 $ ,故估计有 $ 10\% $ 的学生获得一等奖,故 $ \mathrm{C} $ 错误；
对于 $ \mathrm{D} $ ,上四分位数即为第75百分位数,而前3组的频率之和为 $ (0.005+0.01+0.03)×10=0.45 $ ,前4组的频率之和为 $ (0.005+0.01+0.03+0.03)×10=0.75 $ ,
故100名学生成绩的上四分位数为80分,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
5．某高校承办了亚运会志愿者选拔的面试工作.现随机抽取了100名候选者的面试成绩，并分成五组：第一组 $ [45,55) $ ，第二组 $ [55,65) $ ，第三组 $ [65,75) $ ，第四组 $ [75,85) $ ，第五组 $ [85,95] $ ，绘制成如图所示的频率分布直方图.已知第三、四、五组的频率之和为 $ 0.7 $ ，第一组和第五组的频率相同.
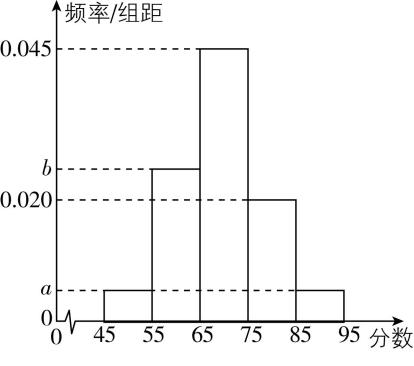
（1） 求 $ a $ ， $ b $ 的值；
（2） 根据组委会要求，本次志愿者选拔录取率为 $ 19\% $ ，请估算被录取至少需要多少分.
（1） 【解】因为第三、四、五组的频率之和为 $ 0.7 $ ,所以 $ (0.045+0.020+a)×10=0.7 $ ,解得 $ a=0.005 $ .
由题意可知, $ (0.005×2+b+0.045+0.020)×10=1 $ ,解得 $ b=0.025 $ .
（2） 由频率分布直方图得 $ [45,55) $ , $ [55,65) $ , $ [65,75) $ , $ [75,85) $ 的频率分别为 $ 0.05 $ , $ 0.25 $ , $ 0.45 $ , $ 0.2 $ ,因为 $ 0.05+0.25+0.45=0.75 < 0.81 $ , $ 0.05+0.25+0.45+0.2=0.95 > 0.81 $ ,所以录取分数应该落在第四组,设录取分数为 $ x $ ,则 $ 0.75+0.02\cdot (x-75)=0.81 $ ,解得 $ x=78 $ ,所以估算被录取至少需要78分.