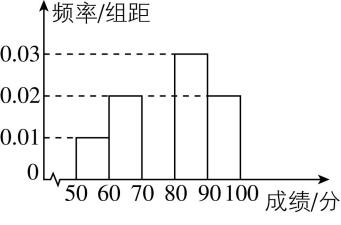
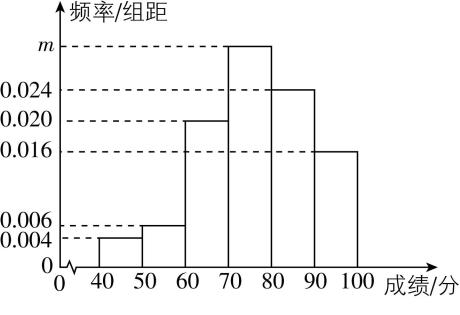
5.将一次学校数学模拟竞赛的成绩统计整理成如图所示的频率分布直方图,记本次模拟竞赛成绩的中位数为 $ a $ ,则 $ a= $ ( )
A. $ 76\dfrac{2}{3} $
B. $ 76\dfrac{1}{3} $
C.75
D. $ 75\dfrac{2}{3} $
由题图可知 $ 0.04+0.06+0.2+10m+0.24+0.16=1 $ ,解得 $ m=0.03 $ ,所以前3组的频率和为 $ 0.04+0.06+0.2=0.3 < 0.5 $ ,前4组的频率和为 $ 0.04+0.06+0.2+0.3=0.6 > 0.5 $ ,故 $ a $ 在第4组,且 $ a=70+\dfrac{0.5-0.3}{0.3}×10=76\dfrac{2}{3} $ .故选 $ \mathrm{A} $ .
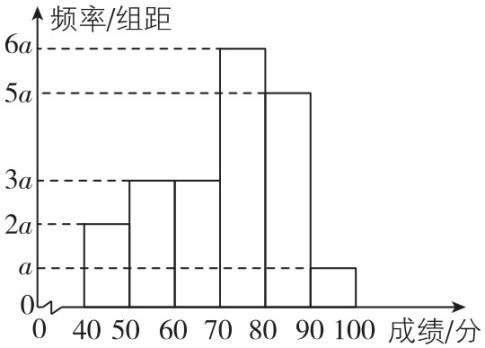
 (多选)
(多选)