10.某玻璃工艺品加工厂有2条生产线用于生产某款产品,每条生产线一天能生产200件该产品,该产品市场评级规定:评分在10分及以上的为 $ A $ 等品,低于10分的为 $ B $ 等品.厂家将 $ A $ 等品售价定为2 000元/件, $ B $ 等品售价定为1 200元/件.下面是检验员在现有生产线上随机抽取的16件产品的评分:
经计算得 $ \overline{x}=\dfrac{1}{16}\underset{i=1}{\sum ^{16}}{x}_{i}=9.98 $ , $ {s}^{2}=\dfrac{1}{16}{\underset{i=1}{\sum ^{16}}({x}_{i}-\overline{x})}^{2}=\dfrac{1}{16}\underset{i=1}{\sum ^{16}}{x}_{i}^{2}-{\overline{x}}^{2}\approx 0.0345 $ ,其中 $ {x}_{i} $ 为抽取的第 $ i $ 件产品的评分, $ i=1 {\rm ,2,3} $ , $ \cdots $ ,16.该厂计划通过增加生产工序来改进生产工艺,已知对一条生产线增加生产工序每年需花费2 000万元,改进后该条生产线产能不变,但生产出的每件产品评分均提高0.05.已知该厂现有一笔2 000万元的资金.
(1) 若厂家用这2 000万元改进一条生产线,根据随机抽取的16件产品的评分,估计改进后该厂生产的所有产品的评分的平均数和方差.
(2) 某金融机构向该厂推销一款年收益率为 $ 8.2\% $ 的理财产品.请你利用所学知识分析,将这2 000万元用于购买该款理财产品所获得的收益,与通过改进一条生产线使产品评分提高所增加的收益相对比,一年后哪种方案的收益更大.(一年按365天计算)
答案:(1) 【解】设一条生产线改进前一天生产出的产品的评分为 $ {y}_{i}(i=1,2,3,\cdots ,200) $ ,改进后生产出的产品的评分为 $ {z}_{i}(i=1,2,3,\cdots ,200) $ ,其中 $ {z}_{i}={y}_{i}+0.05 $ .
用样本估计总体可知 $ \overline{y}=9.98 $ ,
所以 $ \overline{z}=\dfrac{1}{200}\underset{i=1}{\sum ^{200}}{z}_{i}=\dfrac{1}{200}\underset{i=1}{\sum ^{200}}({y}_{i}+0.05)=\overline{y}+0.05=10.03 $ ,
所以估计改进一条生产线后该厂生产的所有产品的评分的平均数为
$ \dfrac{9.98×200+10.03×200}{400}=10.005 $ .
用样本估计总体可知 $ {s}_{y}^{2}\approx 0.0345 $ ,
所以 $ {s}_{z}^{2}=\dfrac{1}{200}\underset{i=1}{\sum ^{200}}{\left({z}_{i}-\overline{z}\right) ^ {2}}=\dfrac{1}{200}\underset{i=1}{\sum ^{200}}[({y}_{i}+0.05)-(\overline{y}+0.05)]^{2}={s}_{y}^{2}\approx 0.0345 $ .
估计改进后该厂生产的所有产品的评分的方差为 $ \dfrac{1}{400}(\underset{i=1}{\sum ^{200}}{y}_{i}^{2}+\underset{i=1}{\sum ^{200}}{z}_{i}^{2})-{10.005}^{2}=\dfrac{1}{400}(\underset{i=1}{\sum ^{200}}{y}_{i}^{2}-200{\overline{y}}^{2}+200{\overline{y}}^{2}+\underset{i=1}{\sum ^{200}}{z}_{i}^{2}-200{\overline{z}}^{2}+200{\overline{z}}^{2})-{10.005}^{2} {\rm ,(*)} $
因为 $ {s}_{y}^{2}=\dfrac{1}{200}\underset{i=1}{\sum ^{200}}{y}_{i}^{2}-{\overline{y}}^{2} $ ,
所以 $ \underset{i=1}{\sum ^{200}}{y}_{i}^{2}-200{\overline{y}}^{2}=200{s}_{y}^{2} $ ,
同理 $ \underset{i=1}{\sum ^{200}}{z}_{i}^{2}-200{\overline{z}}^{2}=200{s}_{z}^{2} $ ,
所以 $ {\rm (*)=} \dfrac{1}{400}(200{s}_{y}^{2}+200{\overline{y}}^{2}+200{s}_{z}^{2}+200{\overline{z}}^{2})-{10.005}^{2} $
$ =\dfrac{{s}_{y}^{2}+{s}_{z}^{2}}{2}+\dfrac{{\overline{y}}^{2}+{\overline{z}}^{2}}{2}-{10.005}^{2} $
$ \approx 0.0345+\dfrac{{9.98}^{2}-{10.005}^{2}}{2}+\dfrac{{10.03}^{2}-{10.005}^{2}}{2} $
$ =0.0345+\dfrac{-0.025×(9.98+10.005)}{2}+\dfrac{0.025×(10.03+10.005)}{2} $
$ =0.0345+{0.025}^{2}=0.035125 $ .
(2) 若将这2 000万元用于改进一条生产线,16件产品中,改进后 $ B $ 等品升为 $ A $ 等品的有6件产品,所以因产品评分提高而增加的比例为 $ \dfrac{6}{16}=\dfrac{3}{8} $ ,
所以将这2 000万元用于改进一条生产线,一年后因产品评分提高而增加的收益为 $ (2000-1200)×\dfrac{3}{8}×200×365-2000×{10}^{4}=190×{10}^{4} $ (元);
将这2 000万元购买该款理财产品,一年后的收益为 $ 2000×{10}^{4}×8.2{\%}=164×{10}^{4} $ (元).
因为 $ 190×{10}^{4} > 164×{10}^{4} $ ,
所以将这2 000万元用于改进一条生产线一年后收益更大.
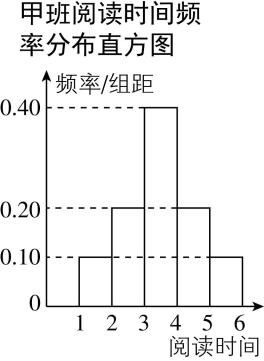

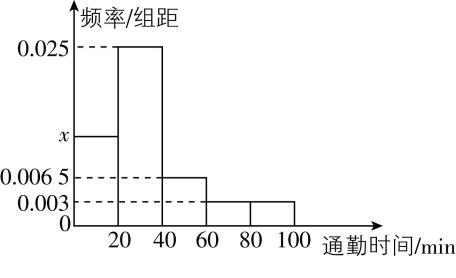 (多选)
(多选)