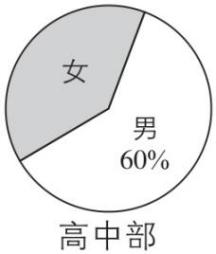
2.某中学初中部共有120名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )

A.128
B.144
C.174
D.167
初中部女教师有 $ 120×70\%=84 $ (人),高中部女教师有 $ 150×(1-60\%)=150×40\%=60 $ (人),所以该校女教师共有 $ 84+60=144 $ (人).故选 $ \mathrm{B} $ .
1.某公司在职员工有1 200人,其中销售人员有400人,研发人员有600人,现采用按比例分配的分层随机抽样的方法抽取120人进行调研,则被抽到的研发人员人数比销售人员人数多( )
A.20
B.30
C.40
D.50
由题意可得被抽到的研发人员有 $ 600×\dfrac{120}{1200}=60 $ (人),销售人员有 $ 400×\dfrac{120}{1200}=40 $ (人),则被抽到的研发人员人数比销售人员人数多 $ 60-40=20 $ .故选 $ \mathrm{A} $ .
2.某中学初中部共有120名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )


A.128
B.144
C.174
D.167
初中部女教师有 $ 120×70\%=84 $ (人),高中部女教师有 $ 150×(1-60\%)=150×40\%=60 $ (人),所以该校女教师共有 $ 84+60=144 $ (人).故选 $ \mathrm{B} $ .
3.嫦娥五号的成功发射,实现了中国航天史上的五个“首次”,某中学为此举行了“讲好航天故事”演讲比赛.若将报名的30位同学编号为 $ {\rm 01,02,} \cdots $ ,30,利用下面的随机数表来决定他们的出场顺序,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,重复的跳过,则选出来的第6个个体的编号为( )
45 67 32 12 12 31 02 01 04
52 15 20 01 12 51 29 32 04
92 34 49 35 82 00 36 23 48
69 69 38 74 81
A.12
B.20
C.29
D.23
依次从数表中读出的有效编号为12,02,01,04,15,20,得到选出来的第6个个体的编号为20,故选 $ \mathrm{B} $ .
4.已知一组数据:5,4,3,3,3,2,1,则下列叙述正确的是( )
A.极差是5
B.平均数是 $ \dfrac{20}{7} $
C.方差是 $ \dfrac{10}{7} $
D.下四分位数为4
将这7个数据从小到大排列为1,2,3,3,3,4,5,
对于 $ \mathrm{A} $ ,极差是 $ 5-1=4 $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,平均数是 $ \dfrac{1+2+3×3+4+5}{7}=\dfrac{21}{7}=3 $ ,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,方差是 $ \dfrac{4+1+0×3+1+4}{7}=\dfrac{10}{7} $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ , $ 7×0.25=1.75 $ ,所以下四分位数为从小到大排列的第2个数,即2,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{C} $ .
5.小军参加少儿体操选拔赛,8位教练员的评分分别为13,14,16,18,18,20,22,23,按比赛规则,计算选手最后得分时,要去掉一个最高分和一个最低分.去掉这组得分中的一个最高分和一个最低分后,下列会发生变化的是( )
A.平均数
B.极差
C.中位数
D.众数
由题可知,去掉一个最高分和一个最低分前后的样本数字特征如下表.
| 原来的8个数据 |
平均数 | $ \dfrac{13+14+16+18+18+20+22+23}{8}=18 $ |
极差 | $ 23-13=10 $ |
中位数 | 18 |
众数 | 18 |
| 去掉一个最高分和一个最低分后的6个数据 |
平均数 | $ \dfrac{14+16+18+18+20+22}{6}=18 $ |
极差 | $ 22-14=8 $ |
中位数 | 18 |
众数 | 18 |
由表可知,只有极差发生变化.故选 $ \mathrm{B} $ .
6.对“小康县”的经济评价标准:①年人均收入不低于7 000元;②年人均食品支出不高于年人均收入的 $ 35\% $ .某县有40万人,年人均收入如表所示,年人均食品支出如图所示,则该县( )
年人均收入/元 | 0 | 2 000 | 4 000 | 6 000 | 8 000 | 10 000 | 12 000 | 16 000 |
人数/万人 | 6 | 3 | 5 | 5 | 6 | 7 | 5 | 3 |
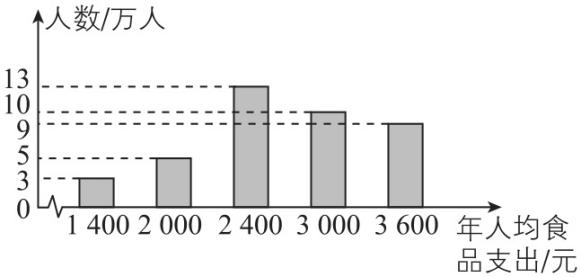
A.是小康县
B.达到标准①,未达到标准②,不是小康县
C.达到标准②,未达到标准①,不是小康县
D.两个标准都未达到,不是小康县
由题中图表可知,年人均收入为 $ (2000×3+4000×5+6000×5+8000×6+10000×7+12000×5+16000×3)÷40=7050 $ (元),达到了标准①;年人均食品支出为 $ (1400×3+2000×5+2400×13+3000×10+3600×9)÷40=2695 $ (元),则年人均食品支出占年人均收入的 $ \dfrac{2695}{7050}×100\%\approx 38.2\% > 35\% $ ,未达到标准②,所以不是小康县.故选 $ \mathrm{B} $ .
7.某地文化和旅游局制定出台推动文旅市场复苏振兴的系列措施,以丰富的旅游业态和高品质的文旅服务不断提升游客出游体验,促进文旅消费增长.现为进一步发展该地文旅市场,提升经济,2025年5月份对该地的部分游客发起满意度调查,从饮食、住宿、交通、服务等方面调查游客满意度,满意度得分采用百分制,统计的综合满意度得分绘制成如下频率分布直方图.若同一组中的数据用该组区间的中点值为代表,则下列结论错误的是( )
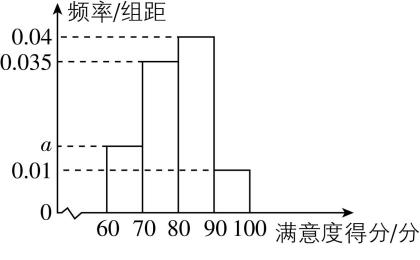
A.频率分布直方图中 $ a=0.015 $
B.2025年5月份该地游客满意度得分的中位数近似值为80
C.2025年5月份该地游客满意度得分的平均数近似值为78
D.若落在 $ [80,90) $ 内的得分的平均值 $ {\overline{x}}_{1}=85 $ ,方差 $ {s}_{1}^{2}=6 $ ,落在 $ [90,100] $ 内的得分的平均值 $ {\overline{x}}_{2}=95 $ ,方差 $ {s}_{2}^{2}=11 $ ,则落在 $ [80,100] $ 内的得分的平均值为87,方差为23
由频率分布直方图得 $ 10(a+0.035+0.04+0.01)=1 $ ,解得 $ a=0.015 $ ,故 $ \mathrm{A} $ 正确;
中位数是累积频率达到0.5时横坐标的值,由 $ 10×(0.015+0.035)=0.5 $ ,可知中位数位于 $ [70,80) $ 和 $ [80,90) $ 的分界线,所以中位数近似值为80,故 $ \mathrm{B} $ 正确;
$ 65×0.15+75×0.35+85×0.4+95×0.1=79.5 $ ,故 $ \mathrm{C} $ 错误;
设落在 $ [80,100] $ 内的得分的平均值为 $ \overline{x} $ ,方差为 $ {s}^{2} $ ,则
$ \overline{x}=\dfrac{0.4{\overline{x}}_{1}+0.1{\overline{x}}_{2}}{0.4+0.1}=\dfrac{0.4×85+0.1×95}{0.5}=87 $ ,
$ {s}^{2}=\dfrac{0.4× [{s}_{1}^{2}+ (\overline{{x}_{1}}-\overline{x})^{2} ]+0.1× [{s}_{2}^{2}+ (\overline{{x}_{2}}-\overline{x})^{2} ]}{0.4+0.1} $
$ =\dfrac{0.4× [6+ (85-87)^{2} ]+0.1× [11+ (95-87)^{2} ]}{0.5} $
$ =23 $ ,故 $ \mathrm{D} $ 正确,故选 $ \mathrm{C} $ .
8.哈希表是一种利用键值的映射关系,将数据存储在特定位置的数据结构.常用的方法之一是“除留余数法”.例如,当除数为3时,键值为13的数据因13除以3余1,应存放于位置1中,从而可直接依据键值快速定位数据位置,多个数据可映射到同一位置(如键值10和13均映射到同一位置).现有一个容量为7个位置(编号 $ 0\sim 6 $ )的哈希表,以除留余数法(除数为7)进行映射,需要存储22个数据.设这7个位置存放的数据个数分别为 $ {a}_{0} $ , $ {a}_{1} $ , $ {a}_{2} $ , $ {a}_{3} $ , $ {a}_{4} $ , $ {a}_{5} $ , $ {a}_{6} $ ,则下列说法中正确的是( )
A.至少有1个位置存放了不少于5个数据
B.若这22个数据的键值恰好是 $ 0\sim 44 $ 间的所有奇数,则 $ {a}_{0}~{a}_{6} $ 的中位数为2
C.若 $ {a}_{0}~{a}_{6} $ 的方差为 $ {s}^{2} $ ,则 $ {s}^{2} $ 的最小值为0,最大值为 $ \dfrac{2904}{49} $
D.若 $ {a}_{0}~{a}_{6} $ 的极差为5,则最多有2个位置没有存放数据
由题意可知, $ {a}_{i} $ 为数据除以7的余数为 $ {\rm i}({\rm i}=0,1,2,3,4,5,6) $ 的数的个数,
对于 $ \mathrm{A} $ 选项, $ 22=7×3+1 $ ,不妨假设这7个位置存放的数据个数分别为3,3,3,3,3,3,4,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ 选项,由题意可知,这些奇数分别为1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,
这些数据除7的余数分别为1,3,5,0,2,4,6,1,3,5,0,2,4,6,1,3,5,0,2,4,6,1,所以 $ {a}_{0}=3 $ , $ {a}_{1}=4 $ , $ {a}_{2}=3 $ , $ {a}_{3}=3 $ , $ {a}_{4}=3 $ , $ {a}_{5}=3 $ , $ {a}_{6}=3 $ ,将 $ {a}_{0}~{a}_{6} $ 这7个数由小到大排列依次为3,3,3,3,3,3,4,中位数为3,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ 选项,由题意可知, $ {a}_{0}~{a}_{6} $ 这7个数的平均数为 $ \overline{x}=\dfrac{22}{7} $ ,且 $ 3 < \dfrac{22}{7} < 4 $ , $ |3-\dfrac{22}{7}| < |4-\dfrac{22}{7}| $ ,因为 $ {a}_{i}\in \boldsymbol{N}(i=0,1,2,3,4,5,6) $ , $ {s}^{2}=\dfrac{1}{7}\underset{i=0}{\sum ^{6}}{\left({a}_{i}-\dfrac{22}{7}\right) ^ {2}} $ ,
当 $ {a}_{0}~{a}_{6} $ 这7个数中有6个3,1个4时, $ {s}^{2} $ 取最小值,即 $ ({s}^{2})_{ \min }=\dfrac{1}{7}× [6×{\left(3-\dfrac{22}{7} \right) ^ {2}}+{\left(4-\dfrac{22}{7} \right) ^ {2}} ]=\dfrac{6}{49} $ ,当 $ {a}_{0}~{a}_{6} $ 这7个数中有6个0,1个22时, $ {s}^{2} $ 取最大值,即 $ ({s}^{2})_{ \max }=\dfrac{1}{7}× [6×{\left(0-\dfrac{22}{7} \right) ^ {2}}+{\left(22-\dfrac{22}{7} \right) ^ {2}} ]=\dfrac{2904}{49} $ ,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ 选项,不妨设 $ {a}_{0}~{a}_{6} $ 这7个数依次为1,6,3,3,3,3,3,
满足极差为5,此时所有位置都有数据,
若存在一些位置没有数据,则 $ {a}_{0}~{a}_{6} $ 这7个数据中的最大值为5,最小值为0,
因为 $ 22=5×4+2 $ ,此时至少需要5个位置存放数据,所以至多有2个位置没有存放数据,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
9.某城市为了解不同年龄段市民对垃圾分类政策的支持情况,对参与问卷调查的市民按老、中、青三个年龄段进行统计,发现三个年龄段的人数比例为 $ 4:3:3 $ .现用按比例分配的分层随机抽样的方法从这些市民中抽取 $ n $ 名进行深入访谈,若抽到老年市民80人,则下列结论正确的是( )(多选)
A.抽到中年市民60人
B.抽到青年市民90人
C. $ n=200 $
D.抽取的中年与青年市民人数之和比老年市民人数多40
设中年市民、青年市民被抽到的人数分别为 $ x $ , $ y $ ,则 $ \dfrac{80}{4}=\dfrac{x}{3}=\dfrac{y}{3} $ ,解得 $ x=y=60 $ ,而 $ n=\dfrac{80}{\dfrac{4}{4+3+3}}=200 $ ,抽取的中年与青年市民人数之和比老年市民人数多 $ 60+60-80=40 $ ,故 $ \mathrm{A}\mathrm{C}\mathrm{D} $ 正确, $ \mathrm{B} $ 错误.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
10.2025年4月23日,在第四届全民阅读大会上正式发布了《2024年度中国数字阅读报告》,公布了我国近五年数字阅读用户规模和网民规模的数据,如图所示,则( )
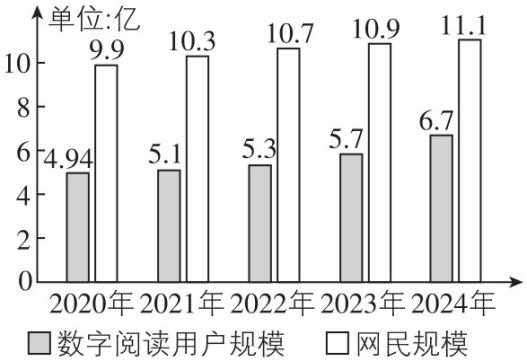 (多选)
(多选)
A.2024年,我国数字阅读用户规模占网民规模的五成以上
B.近五年,我国数字阅读用户规模的增长量比网民规模的增长量大
C.从2020年至2024年,我国数字阅读用户规模逐年递增
D.从2020年至2024年,我国网民规模的增长率逐年递增
对于 $ \mathrm{A} $ ,根据条形图,知2024年我国数字阅读用户规模为6.7亿,网民规模为11.1亿,所以数字阅读用户规模约占网民规模的 $ 60.36\% $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,近五年我国数字阅读用户规模的增长量为 $ 6.7-4.94=1.76 $ 亿,网民规模的增长量为 $ 11.1-9.9=1.2 $ 亿,所以数字阅读用户规模的增长量大于网民规模的增长量,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,根据条形图可以看出,从2020年至2024年,我国数字阅读用户规模逐年递增,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,根据条形图,知从2020年至2021年我国网民规模的增长率为 $ \dfrac{10.3-9.9}{9.9}\approx 0.0404 $ ,从2023年至2024年我国网民规模的增长率为 $ \dfrac{11.1-10.9}{10.9}\approx 0.0183 $ ,增长率减小了,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
11.现有甲、乙、丙三位篮球运动员连续5场篮球比赛得分情况的记录数据,已知三位球员得分情况的数据满足以下条件:
甲球员:5个数据的中位数是26,众数是24;
乙球员:5个数据的中位数是29,平均数是26;
丙球员:5个数据有1个是32,平均数是26,方差是9.6.
根据以上统计数据,下列统计结论一定正确的是( )(多选)
A.甲球员连续5场比赛得分都不低于24分
B.乙球员连续5场比赛得分都不低于24分
C.丙球员连续5场比赛得分都不低于24分
D.丙球员连续5场比赛得分的第60百分位数大于24
设甲球员的5场篮球比赛得分按从小到大的顺序排列为 $ {x}_{1} $ , $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ ,则 $ {x}_{1}\leqslant {x}_{2}\leqslant {x}_{3}\leqslant {x}_{4}\leqslant {x}_{5} $ , $ {x}_{3}=26 $ ,且24至少出现2次,故 $ {x}_{1}={x}_{2}=24 $ , $ \mathrm{A} $ 正确;
设乙球员的5场篮球比赛得分按从小到大的顺序排列为 $ {y}_{1} $ , $ {y}_{2} $ , $ {y}_{3} $ , $ {y}_{4} $ , $ {y}_{5} $ ,
则 $ {y}_{1}\leqslant {y}_{2}\leqslant {y}_{3}\leqslant {y}_{4}\leqslant {y}_{5} $ , $ {y}_{3}=29 $ ,取 $ {y}_{1}=20 $ , $ {y}_{2}=23 $ , $ {y}_{4}=29 $ , $ {y}_{5}=29 $ ,可得其满足题中条件,但有2场得分低于 $ {\rm 24,} \mathrm{B} $ 错误;
设丙球员的5场篮球比赛得分按从小到大的顺序排列为 $ {z}_{1} $ , $ {z}_{2} $ , $ {z}_{3} $ , $ {z}_{4} $ , $ {z}_{5} $ ,
由已知得 $ \dfrac{1}{5} [ ({z}_{1}-26)^{2}+{\left({z}_{2}-26 \right) ^ {2}}+{\left({z}_{3}-26 \right) ^ {2}}+{\left({z}_{4}-26 \right) ^ {2}}+{\left({z}_{5}-26 \right) ^ {2}} ]=9.6 $ ,
所以 $ ({z}_{1}-26)^{2}+{\left({z}_{2}-26 \right) ^ {2}}+{\left({z}_{3}-26 \right) ^ {2}}+{\left({z}_{4}-26 \right) ^ {2}}+{\left({z}_{5}-26 \right) ^ {2}}=48 $ ,
若 $ {z}_{4}\geqslant 32 $ ,则 $ {z}_{5} > 32 $ ,
所以 $ ({z}_{1}-26)^{2}+{\left({z}_{2}-26 \right) ^ {2}}+{\left({z}_{3}-26 \right) ^ {2}}+{\left({z}_{4}-26 \right) ^ {2}}+{\left({z}_{5}-26 \right) ^ {2}} > 72 $ ,矛盾,
所以 $ {z}_{5}=32 $ ,所以 $ ({z}_{1}-26)^{2}+{\left({z}_{2}-26 \right) ^ {2}}+{\left({z}_{3}-26 \right) ^ {2}}+{\left({z}_{4}-26 \right) ^ {2}}=12 $ ,
因为 $ {z}_{1} $ , $ {z}_{2} $ , $ {z}_{3} $ , $ {z}_{4} $ , $ {z}_{5} $ 的平均数为26,所以 $ {z}_{1}+{z}_{2}+{z}_{3}+{z}_{4}=98 $ ,
取 $ {z}_{1}=23 $ , $ {z}_{2}=25 $ , $ {z}_{3}=25 $ , $ {z}_{4}=25 $ ,满足题中条件,但有一场得分低于24分, $ \mathrm{C} $ 错误;
因为 $ 5×60\%=3 $ ,所以丙球员连续5场比赛得分的第60百分位数为 $ \dfrac{{z}_{3}+{z}_{4}}{2} $ ,
若 $ \dfrac{{z}_{3}+{z}_{4}}{2}\leqslant 24 $ ,则 $ \dfrac{{z}_{1}+{z}_{2}}{2}\leqslant 24 $ ,故 $ {z}_{1}+{z}_{2}+{z}_{3}+{z}_{4} < 98 $ ,矛盾,所以 $ \dfrac{{z}_{3}+{z}_{4}}{2} > 24 $ ,所以丙球员连续5场比赛得分的第60百分位数大于 $ {\rm 24,} \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{D} $ .
12.为估计某森林内松鼠的数量,使用以下方法:先随机从森林中捕捉松鼠100只,在每只松鼠的尾巴上做上记号后放回森林,再随机从森林中捕捉50只.若尾巴上有记号的松鼠共有5只,估计此森林内约有松鼠 只.
1 000
估计此森林内约有松鼠 $ 100÷\dfrac{5}{50}=1000 $ (只).
13.若一组样本数据 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{n} $ 的平均数为10,另一组样本数据 $ 2{x}_{1}+4 $ , $ 2{x}_{2}+4 $ , $ \cdots $ , $ 2{x}_{n}+4 $ 的方差为8,则两组样本数据合并为一组样本数据后的平均数是 ,方差是 .(答对一空给3分)
17; 54
由题意可知,数据 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{n} $ 的平均数为10,所以 $ \overline{x}=\dfrac{1}{n}\underset{i=1}{\sum ^{n}}{x}_{i}=10 $ ,则 $ \underset{i=1}{\sum ^{n}}{x}_{i}=10n $ ,
所以数据 $ 2{x}_{1}+4 $ , $ 2{x}_{2}+4 $ , $ \cdots $ , $ 2{x}_{n}+4 $ 的平均数为 $ \overline{{x}^{\prime }}=\dfrac{1}{n}\underset{i=1}{\sum ^{n}}(2{x}_{i}+4)=\dfrac{2}{n}\underset{i=1}{\sum ^{n}}{x}_{i}+4=2×10+4=24 $ ,
方差为 $ {s}^{\prime 2}=\dfrac{1}{n}\underset{i=1}{\sum ^{n}} [ (2{x}_{i}+4 )- (2\overline{x}+4 ){ ]}^{2}=\dfrac{4}{n}\underset{i=1}{\sum ^{n}} ({x}_{i}-10)^{2}=\dfrac{4}{n}\underset{i=1}{\sum ^{n}}{x}_{i}^{2}-\dfrac{4}{n}×20\underset{i=1}{\sum ^{n}}{x}_{i}+\dfrac{4}{n}×n×{10}^{2}=\dfrac{4}{n}\underset{i=1}{\sum ^{n}}{x}_{i}^{2}-400=8 $ ,
解得 $ \underset{i=1}{\sum ^{n}}{x}_{i}^{2}=102n $ .
将两组数据合并后,得到新数据 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{n} $ , $ 2{x}_{1}+4 $ , $ 2{x}_{2}+4 $ , $ \cdots $ , $ 2{x}_{n}+4 $ ,
则其平均数为
$ \overline{{x}^{\prime \prime }}=\dfrac{1}{2n}[\underset{i=1}{\sum ^{n}}{x}_{i}+\underset{i=1}{\sum ^{n}}(2{x}_{i}+4)]=\dfrac{1}{2}×\dfrac{1}{n}\underset{i=1}{\sum ^{n}}(3{x}_{i}+4)=\dfrac{1}{2}(\dfrac{3}{n}\underset{i=1}{\sum ^{n}}{x}_{i}+4)=\dfrac{1}{2}×(3×10+4)=17 $ ,
方差为 $ {s}^{\prime \prime 2}=\dfrac{1}{2n} [\underset{i=1}{\sum ^{n}} ({x}_{i}-17)^{2}+\underset{i=1}{\sum ^{n}} (2{x}_{i}+4-17)^{2} ]=\dfrac{1}{2n} (5\underset{i=1}{\sum ^{n}}{x}_{i}^{2}-86\underset{i=1}{\sum ^{n}}{x}_{i}+458n )=\dfrac{1}{2n} (5×102n-86×10n+458n )=54 $ .
14.支原体肺炎是学龄前儿童及青年人常见的一种肺炎,全年均可发病,以冬季多见,主要通过飞沫传播,潜伏期较长.近期,某班级出现许多学生感染支原体肺炎的现象,为确保班级的正常教学,该班班主任统计了最近一周5天感染支原体肺炎的学生人数,已知这5天的人数互不相等,且5天数据的平均数为 $ \overline{x} $ ,若最后一天的数据不小心被墨水污染,前4天的数据的平均数为 $ \overline{y} $ ,若 $ \overline{x}=\overline{y} $ ,则前4天数据的第75百分位数 (填“大于”“小于”或“等于”)这5天数据的第75百分位数.
大于
已知5天数据的平均数为 $ \overline{x} $ ,前4天的数据的平均数为 $ \overline{y} $ ,且 $ \overline{x}=\overline{y} $ ,
则被污染的数据为 $ 5\overline{x}-4\overline{y}=5\overline{x}-4\overline{x}=\overline{x} $ .
不妨设5天的数据由小到大为 $ {x}_{1} $ , $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ ,其中 $ {x}_{3}=\overline{x} $ ,
因为 $ 5×75\%=3.75 $ ,所以这5天数据的第75百分位数为 $ {x}_{4} $ ,
污染后的数据关系为 $ {x}_{1} < {x}_{2} < {x}_{4} < {x}_{5} $ ,
因为 $ 4×75\%=3 $ ,所以前4天数据的第75百分位数为 $ \dfrac{{x}_{4}+{x}_{5}}{2} $ ,显然 $ {x}_{4} < \dfrac{{x}_{4}+{x}_{5}}{2} $ .
15.某校高中年级举办科技节活动,开设 $ A $ , $ B $ 两个会场,其中每个同学只能去一个会场,且 $ 25\% $ 的同学去 $ A $ 会场,剩下的同学去 $ B $ 会场.已知 $ A $ , $ B $ 会场学生年级及比例情况如下表所示:
| 高一 | 高二 | 高三 |
$ A $ 会场 | $ 50\% $ | $ 40\% $ | $ 10\% $ |
$ B $ 会场 | $ 40\% $ | $ 50\% $ | $ 10\% $ |
记该校高一、高二、高三年级学生所占总人数的比例分别为 $ x $ , $ y $ , $ z $ ,利用按比例分配的分层随机抽样的方法从参加活动的全体学生中抽取一个容量为 $ n $ 的样本.
(1) 求 $ x:y:z $ 的值;
(2) 若抽到的 $ B $ 会场的高二学生有150人,求 $ n $ 的值以及抽到的 $ A $ 会场高一、高二、高三年级的学生人数.
(1) 【解】设该校高一、高二、高三年级的人数分别为 $ a $ , $ b $ , $ c $ ,
则去 $ A $ 会场的学生总数为 $ 0.25(a+b+c) $ ,去 $ B $ 会场的学生总数为 $ 0.75(a+b+c) $ ,
则对应人数如表所示:
| 高一 | 高二 | 高三 |
$ A $ 会场 | $ 0.125(a+b+c) $ | $ 0.1(a+b+c) $ | $ 0.025(a+b+c) $ |
$ B $ 会场 | $ 0.3(a+b+c) $ | $ 0.375(a+b+c) $ | $ 0.075(a+b+c) $ |
则 $ x:y:z=0.425(a+b+c):0.475(a+b+c):0.1(a+b+c)=17:19:4 $ .
(2) 依题意, $ n×0.75×0.5=150 $ ,解得 $ n=400 $ ,则抽到的 $ A $ 会场的学生总人数为 $ 400×0.25=100 $ ,
所以高一年级学生人数为 $ 100×50\%=50 $ ,高二年级学生人数为 $ 100×40\%=40 $ ,高三年级学生人数为 $ 100×10\%=10 $ .
16.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A.1.5小时以上;B. $ 1\sim 1.5 $ 小时;C. $ 0.5\sim 1 $ 小时;D.0.5小时以下.图①,②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题.
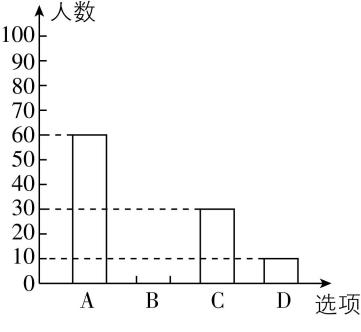
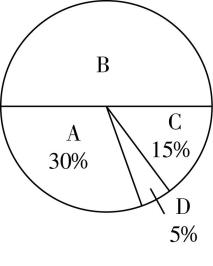
图① 图②
(1) 本次一共调查了多少名学生?
(2) 在图①中将B对应的部分补充完整.
(3) 若该校有3 000名学生,请估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下.
(1) 由题图可知,选A的共60人,占总人数的百分比为 $ 30\% $ ,所以总人数为 $ 60÷30\%=200 $ ,即本次一共调查了200名学生.
(2) 被调查的学生中,选B的有 $ 200-60-30-10=100 $ (人),补充完整的条形统计图如图所示.

(3) $ 3000×5\%=150 $ ,故估计全校有150名学生平均每天参加体育活动的时间在0.5小时以下.
17.某果园试种了 $ A $ , $ B $ 两个品种的桃树各10棵,并在桃树成熟挂果后统计了这20棵桃树的产量如下表,记 $ A $ , $ B $ 两个品种各10棵的产量(单位: $ \mathrm{k}\mathrm{g} $ )的平均数分别为 $ \overline{x} $ 和 $ \overline{y} $ ,方差分别为 $ {s}_{1}^{2} $ 和 $ {s}_{2}^{2} $ .
$ A $ | 60 | 50 | 40 | 60 | 70 | 80 | 80 | 80 | 90 | 90 |
$ B $ | 40 | 60 | 60 | 80 | 80 | 50 | 80 | 80 | 70 | 100 |
(1) 求 $ A $ 品种的10棵桃树产量的第80百分位数;
(2) 求 $ \overline{x} $ , $ \overline{y} $ , $ {s}_{1}^{2} $ , $ {s}_{2}^{2} $ ;
(3) 若果园要大面积种植这两种桃树中的一种,请依据以上计算结果分析选择哪个品种更合适,并说明理由.
(1) 【解】由题意将 $ A $ 品种的10棵桃树产量从小到大排列为40,50,60,60,70,80,80,80,90,90,且 $ 10×0.8=8 $ ,
则第80百分位数为第8位和第9位数的平均数,即 $ \dfrac{80+90}{2}=85 $ .
故 $ A $ 品种的10棵桃树产量的第80百分位数为85.
(2) 由题意可得 $ \overline{x}=\dfrac{1}{10}×(60×2+50+40+70+80×3+90×2)=70 $ ,
则 $ {s}_{1}^{2}=\dfrac{1}{10}× [ (60-70)^{2}×2+ (50-70)^{2}+ (40-70)^{2}+ (70-70)^{2}+ (80-70)^{2}×3+ (90-70)^{2}×2 ]=\dfrac{1}{10}× (100×2+400+900+0+100×3+400×2 )=260 $ ;
$ \overline{y}=\dfrac{1}{10}×(60×2+50+40+70+80×4+100)=70 $ ,
$ {s}_{2}^{2}=\dfrac{1}{10}× [ (60-70)^{2}×2+ (50-70)^{2}+ (40-70)^{2}+ (70-70)^{2}+ (80-70)^{2}×4+ (100-70)^{2} ]=\dfrac{1}{10}× (100×2+400+900+0+100×4+900 )=280 $ .
(3) 种植 $ A $ 品种更合适.由(2)可知 $ \overline{x}=\overline{y}=70 $ , $ {s}_{1}^{2}=260 < {s}_{2}^{2}=280 $ ,所以相比 $ B $ 品种产量 $ A $ 品种产量更稳定.
18.某学校组织“防电信诈骗知识”测试,随机调查400名学生,将他们的测试成绩(满分100分)的统计结果按 $ [50,60),[60,70) $ , $ \cdots $ , $ [90,100] $ 依次分成第一组至第五组,得到如图所示的频率分布直方图.
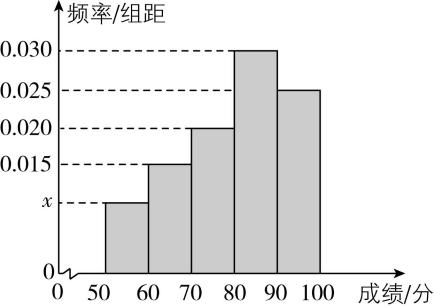
(1) 求图中 $ x $ 的值.
(2) 估计参与这次测试学生的成绩的平均数(同一组中的数据用该组区间的中点值为代表)和第60百分位数.
(3) 现从第三组、第四组和第五组参与测试的学生中用按比例分配的分层随机抽样的方法选取15人,担任学校“防电信诈骗知识”的宣传员.若这15名学校宣传员中来自第三组学生的测试成绩的平均数和方差分别为75和5,来自第四组学生的测试成绩的平均数和方差分别为85和10,来自第五组学生的测试成绩的平均数和方差分别为93和 $ 5.2 $ ,据此估计这次第三组、第四组和第五组所有参与测试学生的成绩的方差.
(1)由题意得 $ (x+0.015+0.020+0.030+0.025)×10=1 $ ,解得 $ x=0.010 $ .
(2) 估计参与这次测试学生的成绩的平均数 $ \overline{u}=10×(55×0.010+65×0.015+75×0.020+85×0.030+95×0.025)=79.5 $ .
由题图得,第一组至第三组的频率之和为 $ (0.01+0.015+0.02)×10=0.45 < 0.6 $ ,第一组至第四组的频率之和为 $ (0.01+0.015+0.02+0.03)×10=0.75 > 0.6 $ ,所以第60百分位数为 $ 80+\dfrac{0.6-0.45}{0.75-0.45}×10=85 $ .
(3) 设第三组、第四组、第五组学生成绩的平均数和方差分别为 $ {\overline{x}}_{3} $ , $ {\overline{x}}_{4} $ , $ {\overline{x}}_{5} $ , $ {s}_{3}^{2} $ , $ {s}_{4}^{2} $ , $ {s}_{5}^{2} $ ,且三组的频率之比为 $ 4:6:5 $ ,则这三组学生的成绩的平均数 $ \overline{x}=\dfrac{75×4+85×6+93×5}{15}=85 $ ,
所以第三组、第四组和第五组所有参与测试学生的成绩的方差
$ {s}^{2}=\dfrac{4}{15} [{s}_{3}^{2}+ ({\overline{x}}_{3}-\overline{x})^{2} ]+\dfrac{6}{15} [{s}_{4}^{2}+ ({\overline{x}}_{4}-\overline{x})^{2} ]+\dfrac{5}{15} [{s}_{5}^{2}+ ({\overline{x}}_{5}-\overline{x})^{2} ] $
$ =\dfrac{4}{15}× [5+ (75-85)^{2} ]+\dfrac{6}{15}× [10+ (85-85)^{2} ]+\dfrac{5}{15}× [5.2+ (93-85)^{2} ] $
$ =\dfrac{826}{15} $ .
19.已知某工厂一区生产车间与二区生产车间均生产某种型号的零件,这两个生产车间生产的该种型号的零件尺寸的频率分布直方图如图所示(每组区间均为左开右闭).

一区生产车间
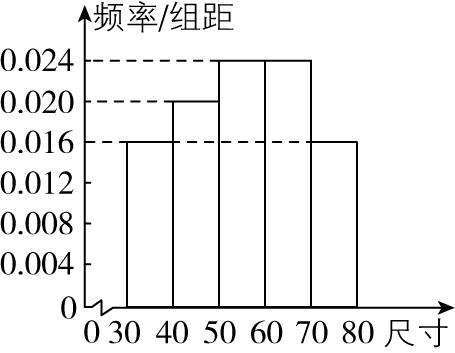
二区生产车间
尺寸大于 $ M $ 的零件用于大型机器中,尺寸小于或等于 $ M $ 的零件用于小型机器中.
(1) 若 $ M=60 $ ,试分别估计该工厂一区生产车间生产的500个该种型号的零件和二区生产车间生产的500个该种型号的零件用于大型机器中的零件个数.
(2) 若 $ M\in (60,70] $ ,现有足够多的来自一区生产车间与二区生产车间的零件,分别用于大型机器、小型机器各5 000台的生产,每台机器仅使用一个该种型号的零件.
方案一:直接将一区生产车间生产的零件用于大型机器中,其中用了尺寸小于或等于 $ M $ 的零件的大型机器每台会使得工厂损失200元;直接将二区生产车间生产的零件用于小型机器中,其中用了尺寸大于 $ M $ 的零件的小型机器每台会使得工厂损失100元.
方案二:重新测量一区生产车间与二区生产车间生产的零件尺寸,并正确匹配型号,重新测量的总费用为35万元.
请写出采用方案一,工厂损失费用的估计值 $ H(M) $ (单位:万元)的表达式,并从工厂损失的角度考虑,选择合理的方案.
(1) 一区生产车间生产的零件尺寸大于60的频率为 $ (0.020+0.024+0.020+0.020)×10=0.84 $ ,
则该工厂一区生产车间生产的500个该种型号的零件用于大型机器中的零件个数为 $ 500×0.84=420 $ .
二区生产车间生产的零件尺寸大于60的频率为 $ (0.024+0.016)×10=0.4 $ ,
则该工厂二区生产车间生产的500个该种型号的零件用于大型机器中的零件个数为 $ 500×0.4=200 $ .
(2) 一区生产车间生产的零件尺寸小于或等于 $ M $ 的频率为
$ 0.004×10+0.012×10+0.02×(M-60)=0.02M-1.04 $ .
二区生产车间生产的零件尺寸大于 $ M $ 的频率为
$ 0.024×(70-M)+0.016×10=1.84-0.024M $ .
故 $ H(M)=(0.02M-1.04)×0.02×5000+(1.84-0.024M)×0.01×5000=0.8M-12 $ .
因为 $ M\in (60,70] $ ,所以 $ H(M)\in (36,44] $ .
又因为采用方案二重新测量的总费用为35万元,
所以从工厂损失的角度考虑,应选择方案二.