1.某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图:
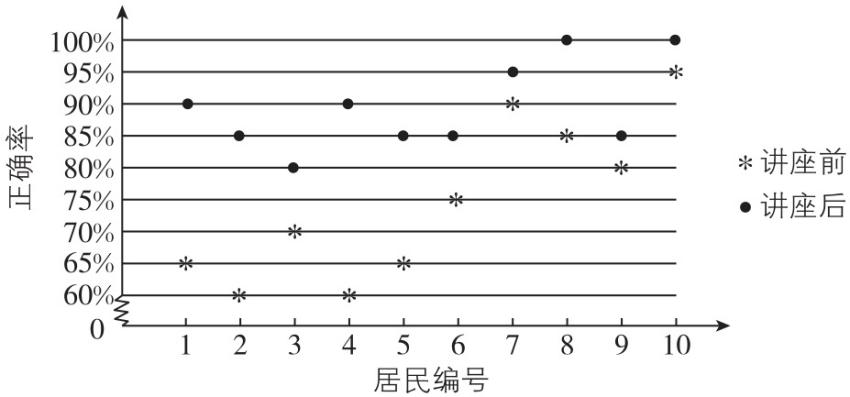
则( )
A.讲座前问卷答题的正确率的中位数小于 $ 70\% $
B.讲座后问卷答题的正确率的平均数大于 $ 85\% $
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
答案:B
解析:对于 $ \mathrm{A} $ ,讲座前问卷答题的正确率的中位数为 $ \dfrac{70\%+75{\%}}{2}=72.5\% $ ,大于 $ 70\% $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,讲座后问卷答题的正确率的平均数为 $ 89.5\% $ ,大于 $ 85\% $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,因为标准差越小,数据越集中,由题图可知,讲座前问卷答题的正确率的标准差大于讲座后正确率的标准差,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,讲座后问卷答题的正确率的极差为 $ 20\% $ ,小于讲座前正确率的极差 $ 35\% $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{B} $ .
2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
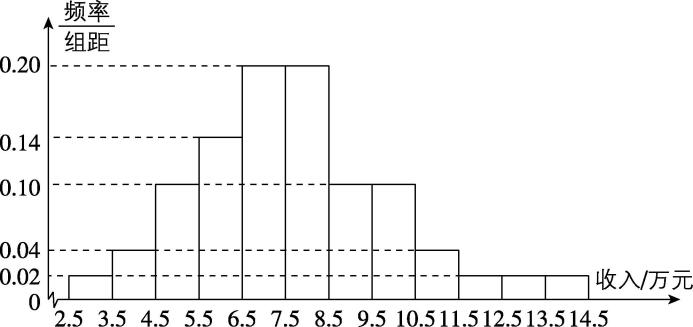
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为 $ 6\% $
B.该地农户家庭年收入不低于10.5万元的农户比率估计为 $ 10\% $
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
答案:C
解析:由频率分布直方图知年收入低于4.5万元的农户比率估计为 $ (0.02+0.04)×1=0.06=6\% $ ,故 $ \mathrm{A} $ 正确;年收入不低于10.5万元的农户比率估计为 $ (0.04+0.02×3)×1=0.10=10\% $ ,故 $ \mathrm{B} $ 正确;该地农户家庭年收入的平均值约为 $ 3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68 > 6.5 $ ,故 $ \mathrm{C} $ 错误;家庭年收入介于4.5万元至8.5万元之间的农户比率约为 $ (0.10+0.14+0.20+0.20)×1=0.64 > 0.5 $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{C} $ .
3.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
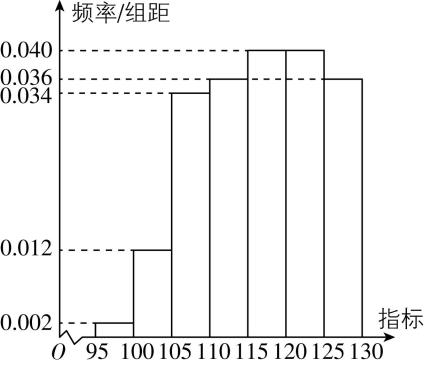

患病者 未患病者
利用该指标制定一个检测标准,需要确定临界值 $ c $ ,将该指标大于 $ c $ 的人判定为阳性,小于或等于 $ c $ 的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为 $ p(c) $ ;误诊率是将未患病者判定为阳性的概率,记为 $ q(c) $ .假设数据在组内均匀分布.以事件发生的频率作为相应事件发生的概率.
(1) 当漏诊率 $ p(c)=0.5\% $ 时,求临界值 $ c $ 和误诊率 $ q(c) $ ;
(2) 设函数 $ f(c)=p(c)+q(c) $ .当 $ c\in [95,105] $ 时,求 $ f(c) $ 的解析式,并求 $ f(c) $ 在区间 $ [95,105] $ 的最小值.
答案:(1) 【解】设 $ X $ 为患病者指标, $ Y $ 为未患病者指标,由患病者指标的频率分布直方图,知 $ p(c)=P(X\leqslant c)=(c-95)×0.002=0.5\% $ ,解得 $ c=97.5 $ .
则 $ q(c)=P(Y > c)=(100-97.5)×0.010+5×0.002=0.035=3.5\% $ .
(2) 当 $ 95\leqslant c\leqslant 100 $ 时,
$ p(c)=(c-95)×0.002 $ , $ q(c)=(100-c)×0.010+5×0.002 $ ,所以 $ f(c)=p(c)+q(c)=-0.008c+0.82 $ ;
当 $ 100 < c\leqslant 105 $ 时,
$ p(c)=5×0.002+(c-100)×0.012 $ , $ q(c)=(105-c)×0.002 $ ,
所以 $ f(c)=p(c)+q(c)=0.01c-0.98 $ .
综上所述, $ f(c)= $
$ \begin{cases}-0.008c+0.82,95\leqslant c\leqslant 100,\\ 0.01c-0.98,100 < c\leqslant 105.\end{cases} $
由一次函数的单调性知,函数 $ f(c) $ 在 $ [95,100] $ 上单调递减,在 $ (100,105] $ 上单调递增,所以 $ f (c)_{ \min }=f (100 )=-0.008×100+0.82=0.02 $ .
解析:
5.某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位: $ \mathrm{k}\mathrm{g} $ )并整理得下表:
亩产量 | $ [900,950) $ | $ [950,1000) $ | $ [1000,1050) $ | $ [1050,1100) $ | $ [1100,1150) $ | $ [1150,1200) $ |
频数 | 6 | 12 | 18 | 30 | 24 | 10 |
根据表中数据,下列结论中正确的是( )
A.100块稻田亩产量的中位数小于 $ 1050\mathrm{k}\mathrm{g} $
B.100块稻田中亩产量低于 $ 1100\mathrm{k}\mathrm{g} $ 的稻田所占比例超过 $ 80\mathrm{\%} $
C.100块稻田亩产量的极差介于 $ 200\mathrm{k}\mathrm{g} $ 至 $ 300\mathrm{k}\mathrm{g} $ 之间
D.100块稻田亩产量的平均值介于 $ 900\mathrm{k}\mathrm{g} $ 至 $ 1000\mathrm{k}\mathrm{g} $ 之间
答案:C
解析: $ \mathrm{A} $ 选项,因为 $ 6+12+18=36 < 50 $ , $ 36+30=66 > 50 $ ,所以100块稻田亩产量的中位数不小于 $ 1050\mathrm{k}\mathrm{g} $ , $ \mathrm{A} $ 错误; $ \mathrm{B} $ 选项,因为100块稻田中亩产量低于 $ 1100\mathrm{k}\mathrm{g} $ 的稻田有66块,所占比例为 $ 66\mathrm{\%} < 80\mathrm{\%} $ ,所以 $ \mathrm{B} $ 错误; $ \mathrm{C} $ 选项,100块稻田亩产量的极差的最大值小于 $ 1200-900=300 $ ,最小值大于 $ 1150-950=200 $ ,所以极差介于 $ 200\mathrm{k}\mathrm{g} $ 至 $ 300\mathrm{k}\mathrm{g} $ 之间, $ \mathrm{C} $ 正确; $ \mathrm{D} $ 选项,同一组中的数据都用左端点值来估计,则这100块稻田亩产量的平均值的最小值为 $ \dfrac{1}{100}×(6×900+12×950+18×1000+30×1050+24×1100+10×1150)=1042 > 1000 $ ,所以平均值不介于 $ 900\mathrm{k}\mathrm{g} $ 至 $ 1000\mathrm{k}\mathrm{g} $ 之间, $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
6.(多选)有一组样本数据 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{6} $ ,其中 $ {x}_{1} $ 是最小值, $ {x}_{6} $ 是最大值,则( )(多选)
A. $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的平均数等于 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{6} $ 的平均数
B. $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的中位数等于 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{6} $ 的中位数
C. $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的标准差不小于 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{6} $ 的标准差
D. $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的极差不大于 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{6} $ 的极差
答案:BD
解析:对于选项 $ \mathrm{A} $ , $ \because {x}_{1} $ , $ {x}_{6} $ 不确定, $ \therefore {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{6} $ 的平均数不确定,如1,2,2,2,2,4的平均数不等于2,2,2,2的平均数,故 $ \mathrm{A} $ 错误;
对于选项 $ \mathrm{B} $ ,不妨设 $ {x}_{2}\leqslant {x}_{3}\leqslant {x}_{4}\leqslant {x}_{5} $ ,则 $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的中位数为 $ \dfrac{{x}_{3}+{x}_{4}}{2} $ , $ {x}_{1} $ , $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ , $ {x}_{6} $ 的中位数为 $ \dfrac{{x}_{3}+{x}_{4}}{2} $ ,故 $ \mathrm{B} $ 正确;
对于选项 $ \mathrm{C} $ , $ \because {x}_{1} $ , $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ , $ {x}_{6} $ 的波动性不小于 $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的波动性,
$ \therefore {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的标准差不大于 $ {x}_{1} $ , $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ , $ {x}_{6} $ 的标准差,故 $ \mathrm{C} $ 错误;
对于选项 $ \mathrm{D} $ ,不妨设 $ {x}_{2}\leqslant {x}_{3}\leqslant {x}_{4}\leqslant {x}_{5} $ ,则 $ {x}_{1}\leqslant {x}_{2}\leqslant {x}_{3}\leqslant {x}_{4}\leqslant {x}_{5}\leqslant {x}_{6} $ , $ \therefore {x}_{5}-{x}_{2}\leqslant {x}_{6}-{x}_{1} $ ,即 $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ 的极差不大于 $ {x}_{1} $ , $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4} $ , $ {x}_{5} $ , $ {x}_{6} $ 的极差,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{B}\mathrm{D} $ .
8.某厂为比较甲、乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率.甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为 $ {x}_{i} $ , $ {y}_{i}(i=1,2,\cdots ,10) $ .试验结果如下:
试验序号 $ i $ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
伸缩率 $ {x}_{i} $ | 545 | 533 | 551 | 522 | 575 | 544 | 541 | 568 | 596 | 548 |
伸缩率 $ {y}_{i} $ | 536 | 527 | 543 | 530 | 560 | 533 | 522 | 550 | 576 | 536 |
记 $ {z}_{i}={x}_{i}-{y}_{i}(i=1,2,\cdots ,10) $ ,记 $ {z}_{1} $ , $ {z}_{2} $ , $ \cdots $ , $ {z}_{10} $ 的样本平均数为 $ \overline{z} $ ,样本方差为 $ {s}^{2} $ .
(1) 求 $ \overline{z} $ , $ {s}^{2} $ ;
(2) 判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高 $ ( $ 如果 $ \overline{z}\geqslant 2\sqrt{\dfrac{{s}^{2}}{10}} $ ,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高 $ ) $ .
答案:(1) 【解】因为 $ {z}_{i}={x}_{i}-{y}_{i}(i=1,2,\cdots ,10) $ ,
所以 $ {z}_{1}=9 $ , $ {z}_{2}=6 $ , $ {z}_{3}=8 $ , $ {z}_{4}=-8 $ , $ {z}_{5}=15 $ , $ {z}_{6}=11 $ , $ {z}_{7}=19 $ , $ {z}_{8}=18 $ , $ {z}_{9}=20 $ , $ {z}_{10}=12 $ ,
所以 $ \overline{z}=\dfrac{1}{10}×(9+6+8-8+15+11+19+18+20+12)=11 $ ,
所以 $ {s}^{2}=\dfrac{1}{10}×(4+25+9+361+16+0+64+49+81+1)=61 $ .
(2) 因为 $ 2\sqrt{\dfrac{{s}^{2}}{10}}=2×\sqrt{\dfrac{61}{10}}=\sqrt{24.4} < 11 $ ,即 $ 2\sqrt{\dfrac{{s}^{2}}{10}} < \overline{z} $ ,
所以甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.
解析:
1.某公司对来应聘的人进行笔试,统计出200名应聘者的笔试成绩,整理得到下表:
组号 | 1 | 2 | 3 | 4 | 5 | 6 |
成绩分组 | $ [40,50) $ | $ [50,60) $ | $ [60,70) $ | $ [70,80) $ | $ [80,90) $ | $ [90,100] $ |
累积频率 | 0.05 | 0.15 | $ a $ | $ a+0.30 $ | $ 2a+0.10 $ | $ 2a+0.30 $ |
注:第 $ n $ 组的累积频率指的是前 $ n $ 组的频率之和.
若公司计划150人进入面试,则估计参加面试的最低分数线为 .
解析:由第6组累积频率为1得, $ 2a+0.3=1 $ ,则 $ a=0.35 $ .
由 $ \dfrac{150}{200}=0.75 $ 知,面试的最低分数线为笔试成绩从低到高排列的 $ 25\% $ 分位数 $ m $ ,由题表知,笔试成绩在 $ [40,60) $ 与 $ [40,70) $ 的累积频率分别为 $ 0.15 $ , $ 0.35 $ ,
故 $ \dfrac{m-60}{70-60}=\dfrac{0.25-0.15}{0.35-0.15} $ ,解得 $ m=65 $ ,
从而可估计参加面试的最低分数线为65.
2.已知一组统计数据 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{n} $ 的平均数为 $ \overline{x} $ ,方差为 $ {s}^{2} $ ,则函数 $ f(x)=\underset{i=1}{\sum ^{n}}{\left(x-{x}_{i}\right) ^ {2}} $ 的最小值为 .
解析:由 $ \overline{x}=\dfrac{1}{n}\underset{i=1}{\sum ^{n}}{x}_{i} $ ,得 $ {s}^{2}=\dfrac{1}{n}\underset{i=1}{\sum ^{n}} ({x}_{i}-\overline{x})^{2}=\dfrac{1}{n} (\underset{i=1}{\sum ^{n}}{x}_{i}^{2}-2\overline{x}\underset{i=1}{\sum ^{n}}{x}_{i}+n{\overline{x}}^{2} )=\dfrac{1}{n} (\underset{i=1}{\sum ^{n}}{x}_{i}^{2}-n{\overline{x}}^{2} ) $ ,
则 $ \underset{i=1}{\sum ^{n}}{x}_{i}^{2}=n({s}^{2}+{\overline{x}}^{2}) $ ,
故 $ f(x)=\underset{i=1}{\sum ^{n}}{\left(x-{x}_{i}\right) ^ {2}}=n{x}^{2}-2x\underset{i=1}{\sum ^{n}}{x}_{i}+\underset{i=1}{\sum ^{n}}{x}_{i}^{2}=n{x}^{2}-2n\overline{x}\cdot x+\underset{i=1}{\sum ^{n}}{x}_{i}^{2}=n{\left(x-\overline{x}\right) ^ {2}}+n{s}^{2}\geqslant n{s}^{2} $ ,当且仅当 $ x=\overline{x} $ 时等号成立.所以函数 $ f(x)=\underset{i=1}{\sum ^{n}}{\left(x-{x}_{i}\right) ^ {2}} $ 的最小值为 $ n{s}^{2} $ .
3.某网络公司为了提升服务质量,从会员库中随机抽取 $ n $ 名会员进行线上问卷调查,将会员的评分(满分10分)从低到高分为四个等级:
会员评分 | $ [4,5) $ | $ [5,6) $ | $ [6,7) $ | $ [7,8) $ | $ [8,9) $ | $ [9,10] $ |
满意等级 | 不满意 | 一般 | 满意 | 非常满意 |
并绘制出如图所示的频率分布直方图.已知调查评分在 $ [7,8) $ 内的会员人数为40.
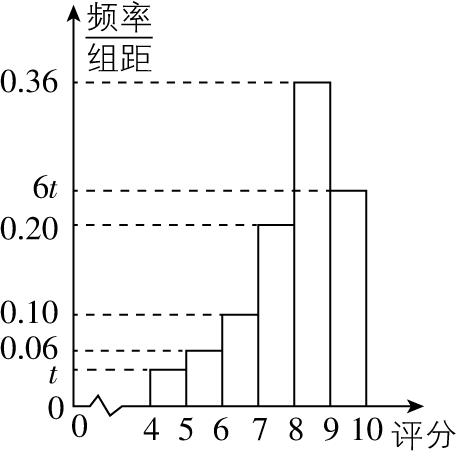
(1) 求样本容量 $ n $ 及频率分布直方图中的 $ t $ 值.
(2) 若该公司以抽取的样本为参考,每组数据以该组评分的区间中点值为代表进行评估:
(ⅰ) 若会员满意度评分的平均值 $ \overline{x} $ 低于8分,则需要提升公司产品的体验感,否则全力开发新产品.根据所学的统计知识,判断该公司应采用的运营策略,并说明理由.
(ⅱ) 记会员评分的样本标准差为 $ s $ ,试估计会员总体评分在区间 $ [\overline{x}-s,\overline{x}+s) $ 内的人数的百分比.
(参考数据: $ {1.29}^{2}\approx 1.66 $ , $ {1.31}^{2}\approx 1.72 $ , $ {1.32}^{2}\approx 1.74 $ , $ {1.33}^{2}\approx 1.77 $ )
答案:(1) 【解】由频率分布直方图可知,评分在 $ [7,8) $ 内的频率 $ f=1×0.20=0.2 $ ,故样本容量 $ n=\dfrac{40}{0.2}=200 $ .由 $ (t+0.06+0.10+0.20+6t+0.36)×1=1 $ ,得 $ t=0.04 $ .
(2) 各组评分的区间中点值分别为 $ 4.5 $ , $ 5.5 $ , $ 6.5 $ , $ 7.5 $ , $ 8.5 $ , $ 9.5 $ .
(2) (ⅰ) 会员满意度评分的平均值
$ \overline{x}=4.5×0.04+5.5×0.06+6.5×0.10+7.5×0.20+8.5×0.36+9.5×0.24=8 $ ,故该公司应全力开发新产品.
(ⅱ) 因为方差 $ {s}^{2}={\left(4.5-\overline{x}\right) ^ {2}}×0.04+{\left(5.5-\overline{x}\right) ^ {2}}×0.06+{\left(6.5-\overline{x}\right) ^ {2}}×0.10+{\left(7.5-\overline{x}\right) ^ {2}}×0.20+{\left(8.5-\overline{x}\right) ^ {2}}×0.36+{\left(9.5-\overline{x}\right) ^ {2}}×0.24=1.77 $ ,则 $ s\approx 1.33 $ ,故 $ \overline{x}-s\approx 6.67 $ , $ \overline{x}+s\approx 9.33 $ .
区间 $ [6,7) $ 内评分不小于6.67的频率 $ m $ 满足 $ \dfrac{7-6.67}{7-6}=\dfrac{m}{0.10} $ ,解得 $ m=0.033 $ ,区间 $ [9,10) $ 内评分小于9.33的频率 $ n $ 满足 $ \dfrac{9.33-9}{10-9}=\dfrac{n}{0.24} $ ,即 $ n=0.0792 $ ,
所以样本在区间 $ [\overline{x}-s,\overline{x}+s) $ 内的频率为 $ m+0.20+0.36+n=0.6722 $ ,
因此用样本估计总体知,会员总体评分在区间 $ [\overline{x}-s,\overline{x}+s) $ 内的人数的百分比约为 $ 67.22\% $ .
解析:




