①甲直接结束掷骰子,换由乙掷骰子一次,向上的点数记为 $ b $ ,若 $ a+b\leqslant 6 $ ,则乙赢,否则甲赢,游戏结束.
②甲再掷一次骰子,向上的点数记为 $ c $ ,若 $ a+c > 6 $ ,则乙赢,游戏结束;若 $ a+c\leqslant 6 $ ,甲结束掷骰子,换由乙掷骰子一次,向上的点数记为 $ d $ ,若 $ a+c+d\leqslant 6 $ ,则乙赢,否则甲赢,游戏结束.问:
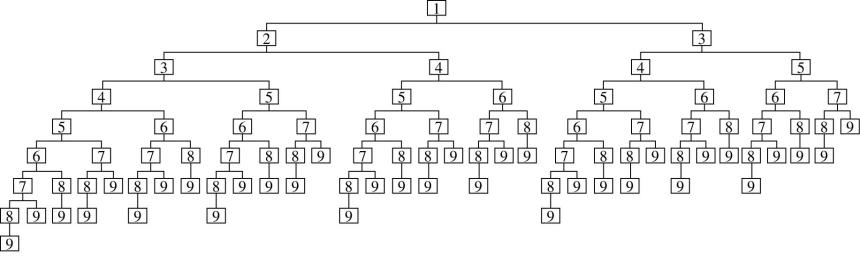
(1) 若甲只掷骰子1次,求甲赢的概率.
(2) 若甲掷骰子2次,求甲赢的概率.
答案:(1) 【解】若甲只掷骰子1次,甲赢的情况如下:
甲掷出向上的点数为1,乙掷出向上的点数为6,此时有1种情况;
甲掷出向上的点数为2,乙掷出向上的点数为6,5,此时有2种情况;
甲掷出向上的点数为3,乙掷出向上的点数为6,5,4,此时有3种情况;
依此类推,甲赢的情况共有 $ 1+2+3+4+5+6=21 $ 种,
故甲赢的概率为 $ \dfrac{21}{36}=\dfrac{7}{12} $ .
(2) 若甲掷骰子2次,甲赢的情况如下:
①甲第1次掷骰子向上的点数为1.
第2次掷骰子向上的点数为1,乙掷骰子向上的点数为6,5,此时有2种情况;
第2次掷骰子向上的点数为2,乙掷骰子向上的点数为6,5,4,此时有3种情况;
依此类推,
第2次掷骰子向上的点数为5,乙掷骰子向上的点数为6,5,4,3,2,1,此时有6种情况.
以上共有 $ 2+3+4+5+6=20 $ 种情况.
②甲第1次掷骰子向上的点数为2.
第2次掷骰子向上的点数为1,乙掷骰子向上的点数为6,5,4,此时有3种情况;
第2次掷骰子向上的点数为2,乙掷骰子向上的点数为6,5,4,3,此时有4种情况;
第2次掷骰子向上的点数为3,乙掷骰子向上的点数为6,5,4,3,2,此时有5种情况;
第2次掷骰子向上的点数为4,乙掷骰子向上的点数为6,5,4,3,2,1,此时有6种情况,
以上共有 $ 3+4+5+6=18 $ 种情况.
依此类推,③甲第1次掷骰子向上的点数为3时,甲赢的情况有 $ 4+5+6=15 $ 种.
④甲第1次掷骰子向上的点数为4时,甲赢的情况有 $ 5+6=11 $ 种.
⑤甲第1次掷骰子向上的点数为5时,甲赢的情况有6种.
综上,甲掷骰子2次且甲赢的情况总数为 $ 20+18+15+11+6=70 $ .
故甲赢的概率为 $ \dfrac{70}{{6}^{3}}=\dfrac{35}{108} $ .
(3) 当甲第一次掷骰子向上的点数为 $ a $ 时,
甲选择①,若甲赢,则乙掷骰子向上的点数为 $ {\rm 6,5,4,} \cdots $ , $ 7-a $ ,共 $ a $ 种,
而乙掷骰子向上的点数共6种情况,则甲赢的概率 $ {P}_{1}=\dfrac{a}{6} $ .
甲选择②,若甲赢,则甲第二次掷骰子向上的点数为 $ {\rm 1,2,} \cdots $ , $ 6-a $ ,共 $ 6-a $ 种,
若甲第二次掷骰子向上的点数为1时,则乙掷骰子向上的点数为 $ {\rm 6,5,4,} \cdots $ , $ 6-a $ ,共 $ a+1 $ 种;
若甲第二次掷骰子向上的点数为2时,则乙掷骰子向上的点数为 $ {\rm 6,5,4,} \cdots $ , $ 5-a $ ,共 $ a+2 $ 种;
……
若甲第二次掷骰子向上的点数为 $ 6-a $ 时,则乙掷骰子向上的点数为6,5,4,3,2,1,共6种,
所以甲赢的情况的总数为 $ (a+1)+(a+2)+\cdots +6=\dfrac{(a+1+6)(6-a)}{2}=\dfrac{(a+7)(6-a)}{2} $ ,
而甲第二次掷骰子、乙掷骰子的可能情况各为6种,则甲赢的概率
$ {P}_{2}=\dfrac{(a+7)(6-a)}{2×{6}^{2}}=\dfrac{(a+7)(6-a)}{72} $ .
令 $ {P}_{1} > {P}_{2} $ ,即 $ \dfrac{a}{6} > \dfrac{(a+7)(6-a)}{72} $ ,化简得 $ {a}^{2}+13a-42 > 0 $ ,解得 $ a > \dfrac{-13+\sqrt{337}}{2} $ .
因为 $ 2 < \dfrac{-13+\sqrt{337}}{2} < 3(a\in {\boldsymbol{N}}^{\ast }) $ ,且 $ a\leqslant 6 $ ,所以 $ a=3 $ 或4或5或6.
综上,当甲掷骰子向上的点数为3或4或5或6时,甲选择①赢得游戏的概率更大.
 (多选)
(多选)