7.某市四所重点中学进行高二期中联考,共有5 000名学生参加,为了了解数学学科的学习情况,现从中随机地抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
$ [80,90) $ | ① | ② |
$ [90,100) $ |
| 0.050 |
$ [100,110) $ |
| 0.200 |
$ [110,120) $ | 36 | 0.300 |
$ [120,130) $ |
| 0.275 |
$ [130,140) $ | 12 | ③ |
$ [140,150] $ |
| 0.050 |
合计 |
| ④ |
(1) 根据上面的频率分布表,计算①②③④处的数字分别为 , , , .
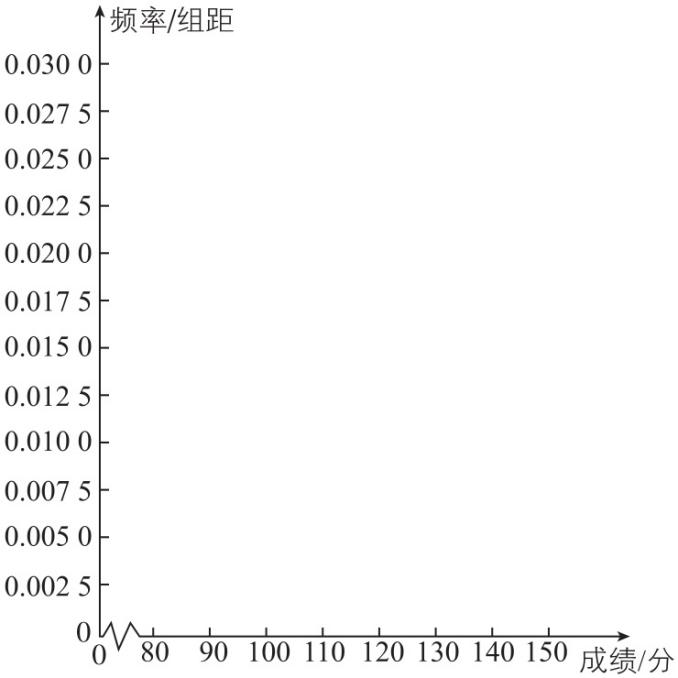
(2) 画出频率分布直方图.
(3) 根据题中的信息估计总体:
① 成绩在120分及以上的学生人数;
② 成绩在 $ [126,150] $ 内的概率.
(1) 3; $ 0.025 $ ; $ 0.100 $ ;1
(2) 【解】频率分布直方图如图所示.

(3) ① 成绩在120分及以上的学生人数约为 $ (0.275+0.100+0.050)×5000=2125 $ .
② 成绩在 $ [126,150] $ 内的概率约为 $ 0.4×0.275+0.100+0.050=0.26 $ .
(1) 由题表可知,共抽取了 $ \dfrac{36}{0.300}=120 $ 名学生,③处的数字为 $ \dfrac{12}{120}=0.100 $ ,②处的数字是 $ 1-0.050-0.200-0.300-0.275-0.100-0.050=0.025 $ ,①处的数字是 $ 0.025×120=3 $ ,④处的数字是1.
故①②③④处的数字分别为 $ {\rm 3,} 0.025 $ , $ 0.100 {\rm ,1} $ .