专题9 概率与统计的综合应用

一、刷难关

1．某地区公共卫生部门为了调查本地区中学生的吸烟情况，对随机抽出的200名学生进行了调查.调查中使用了下面两个问题：

问题一：你的生日日期是不是奇数？

问题二：你是否经常吸烟？

调查者设计了一个随机化装置：一个装有大小、形状、质量完全一样的50个白球和50个红球的袋子，每个被调查者随机从袋中摸取1个球（摸出的球再放回袋中），摸到白球的学生如实回答第一个问题，摸到红球的学生如实回答第二个问题，回答“是”的人往一个盒子中放一个小石子，回答“否”的人什么都不要做，最后收集回来60个小石子，则可以估计出该地区经常吸烟的中学生所占的百分比约为（假设一年为365天，其中日期为奇数的天数为186）（      ）

A． $ 9\% $

B． $ 14\% $

C． $ 16\% $

D． $ 32\% $

答案：A
解析：

因为从一个装有大小、形状、质量完全一样的50个白球和50个红球的袋子中,随机摸出1个球,摸到白球和红球的概率都为 $ \dfrac{1}{2} $ ,

因此,这200人中,回答了第一个问题的大约有100人,

而一年365天中,日期为奇数的有186天,所以对第一个问题回答“是”的概率为 $ \dfrac{186}{365}\approx 0.51 $ ,

所以这100名回答第一个问题的学生中,约有51人回答了“是”,

从而可以估计,回答第二个问题的100人中,约有9人回答了“是”,

所以可以估计出该地区经常吸烟的中学生所占的百分比为 $ 9\% $ .故 $ \mathrm{A} $ 正确.故选 $ \mathrm{A} $ .

2．某课外实践小组随机调查了该市的10名外卖骑手，统计他们的日单量（平均每天送的外卖单数），数据如表：

31

37

38

32

33

42

24

20

37

26

（1） 试用频率估计概率，估计该市的外卖骑手日单量大于30的概率.

（2） 求这10名外卖骑手日单量的平均数和方差.

（3） 若表中第一行数据对应的外卖骑手来自甲公司，第二行数据对应的外卖骑手来自乙公司，试判断：哪家公司的外卖骑手日单量的差异更大?（直接给出结论即可，不需要写计算过程）

答案：

（1） 【解】10名外卖骑手中有7人的日单量大于30,频率为 $ \dfrac{7}{10} $ ,

因此估计该市的外卖骑手日单量大于30的概率为 $ \dfrac{7}{10} $ .

（2） 平均数为 $ \overline{x}=30+\dfrac{1}{10}×(1+7+8+2+3+12-6-10+7-4)=32 $ .

方差为 $ {s}^{2}=\dfrac{1}{10}× [ (-1)^{2}+{5}^{2}+{6}^{2}+0+{1}^{2}+{10}^{2}+ (-8)^{2}+ (-12)^{2}+{5}^{2}+ (-6)^{2} ]=43.2 $ .

（3） 乙公司的外卖骑手日单量的差异更大,理由如下：

甲公司的外卖骑手日单量的极差为 $ 38-31=7 $ ,

乙公司的外卖骑手日单量的极差为 $ 42-20=22 $ ,

由于 $ 22 > 7 $ ,故乙公司的外卖骑手日单量的差异更大.

解析：

3．某学校高一年级组织了1 200名学生参加线上航天知识竞赛活动，现从中抽取200名学生，记录他们的首轮竞赛成绩并作出如图所示的频率分布直方图（每组为左闭右开的区间），请据图回答下列问题.

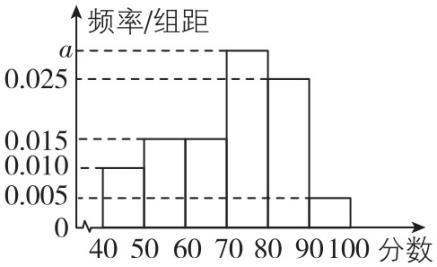
试题资源网 https://stzy.com

（1） 若从成绩低于60分的同学中按分层抽样的方法抽取10人的成绩，求10人中成绩低于50分的人数；

（2） 求 $ a $ 的值，并以样本估计总体，估计该校学生首轮竞赛成绩的平均数及中位数；

（3） 由首轮竞赛成绩确定甲、乙、丙三位同学参加第二轮的复赛，已知甲复赛获优秀等级的概率为 $ \dfrac{2}{3} $ ，乙复赛获优秀等级的概率为 $ \dfrac{3}{4} $ ，丙复赛获优秀等级的概率为 $ \dfrac{1}{2} $ ，甲、乙、丙是否获优秀等级互不影响，求三人中至少有两位同学复赛获优秀等级的概率.

答案：

（1） 【解】因为抽取的200名学生中, 成绩低于50分的人数为 $ 0.010×10×200=20 $ ,

成绩在 $ [50,60) $ 分的人数为 $ 0.015×10×200=30 $ ,所以从成绩低于60分的同学中按分层抽样的方法抽取10人的成绩,其中低于50分的人数为 $ 10×\dfrac{20}{20+30}=4 $ .

（2） 由 $ (0.005+0.010+0.015+0.015+0.025+a)×10=1 $ ,解得 $ a=0.03 $ .

平均数 $ \overline{x}=45×0.10+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71 $ （分）.

因为成绩低于70分的频率为 $ (0.01+0.015+0.015)×10=0.4 $ ,成绩低于80分的频率为 $ (0.01+0.015+0.015+0.03)×10=0.7 $ ,

所以中位数位于 $ [70,80) $ 内,则中位数为 $ 70+\dfrac{0.5-0.4}{0.03}=\dfrac{220}{3} $ （分）.

（3） 三人中至少有两位同学复赛获优秀等级的概率 $ P=\dfrac{2}{3}×\dfrac{3}{4}×\dfrac{1}{2}+\dfrac{2}{3}×\dfrac{1}{4}×\dfrac{1}{2}+\dfrac{1}{3}×\dfrac{3}{4}×\dfrac{1}{2}+\dfrac{2}{3}×\dfrac{3}{4}×\dfrac{1}{2}=\dfrac{17}{24} $ .

解析：