第十章素养检测

1．为了推广一种新饮料，某饮料生产企业开展了有奖促销活动：将8瓶该种饮料装一箱，其中有2瓶能够中奖.现从一箱该饮料中随机抽取2瓶，则下列两个事件互斥但不对立的是（）

A．“至少有1瓶中奖”与“2瓶都中奖”

B．“至多有1瓶中奖”与“2瓶都中奖”

C．“恰有1瓶中奖”与“2瓶都不中奖”

D．“恰有1瓶中奖”与“至多有1瓶中奖”

答案：C

解析：

对于 $ \mathrm{A} $ ,“至少有1瓶中奖”与“2瓶都中奖”可以同时发生,则“至少有1瓶中奖”与“2瓶都中奖”不是互斥事件,所以 $ \mathrm{A} $ 错误；

对于 $ \mathrm{B} $ ,“至多有1瓶中奖”与“2瓶都中奖”是对立事件,所以 $ \mathrm{B} $ 错误；

对于 $ \mathrm{C} $ ,“恰有1瓶中奖”与“2瓶都不中奖”是互斥但不对立事件,所以 $ \mathrm{C} $ 正确；

对于 $ \mathrm{D} $ ,“恰有1瓶中奖”与“至多有1瓶中奖”可以同时发生,则“恰有1瓶中奖”与“至多有1瓶中奖”不是互斥事件,所以 $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .

2．下列说法正确的是（）

A．若一批产品的次品率为 $ \dfrac{1}{10} $ ，则从中任取10件，必有1件是次品

B．天气预报：“明天降雨的概率为 $ 90\% $ ”，则明天可能不下雨

C．一名篮球运动员，号称“百发百中”，若罚球三次，则不会出现三次都投不中的情况

D．做8次抛硬币的试验，结果5次出现正面，则抛一枚硬币出现正面的概率是 $ \dfrac{5}{8} $

答案：B

解析：

对于 $ \mathrm{A} $ ,次品率描述的是次品的可能情况,故 $ \mathrm{A} $ 错误；

对于 $ \mathrm{B} $ ,天气预报：“明天降雨的概率为 $ 90\% $ ”,则明天可能不下雨,故 $ \mathrm{B} $ 正确；

对于 $ \mathrm{C} $ ,罚球三次,有可能出现三次都投不中的情况,故 $ \mathrm{C} $ 错误；

对于 $ \mathrm{D} $ ,做8次抛硬币的试验,结果5次出现正面,则抛一枚硬币出现正面的频率是 $ \dfrac{5}{8} $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{B} $ .

3．对空中飞行的飞机连续射击两次，每次发射一枚炮弹，设 $ A= $ “两次都击中飞机”， $ B= $ “两次都没击中飞机”， $ C= $ “恰有一枚炮弹击中飞机”， $ D= $ “至少有一枚炮弹击中飞机”，则下列关系不正确的是（）

A． $ A\subseteq D $

B． $ B\cap D=⌀ $

C． $ A\cup C=D $

D． $ A\cup B=B\cup D $

答案：D

解析：

“恰有一枚炮弹击中飞机”指第一枚击中第二枚没击中或第一枚没击中第二枚击中,“至少有一枚炮弹击中飞机”包含两种情况：恰有一枚炮弹击中、两枚炮弹都击中，故 $ A\subseteq D $ , $ A\cup C=D $ , $ B $ , $ D $ 为互斥事件, $ B\cap D=⌀ $ ； $ A\cup B= $ “两次都击中或者都没击中飞机”, $ B\cup D $ 为必然事件,这两者不相等.故选 $ \mathrm{D} $ .

4．从长度为1，3，5，7，9的5条线段中任取3条，则这3条线段能构成一个三角形的概率为（）

A． $ \dfrac{1}{10} $

B． $ \dfrac{1}{5} $

C． $ \dfrac{3}{10} $

D． $ \dfrac{2}{5} $

答案：C

解析：

从5条线段中任取3条的所有样本点有10个,即 $ (1,3,5) $ , $ (1,3,7) $ , $ (1,3,9) $ , $ (1,5,7) $ , $ (1,5,9) $ , $ (1,7,9) $ , $ (3,5,7) $ , $ (3,5,9) $ , $ (3,7,9) $ , $ (5,7,9) $ ,

其中能构成三角形的样本点有3个,即 $ (3,5,7) $ , $ (3,7,9) $ , $ (5,7,9) $ ,

故所求概率 $ P=\dfrac{3}{10} $ .故选 $ \mathrm{C} $ .

6．下列说法正确的是（）

A．若 $ P(A) > 0 $ , $ P(B) > 0 $ ，则事件 $ A $ ， $ B $ 相互独立与事件 $ A $ ， $ B $ 互斥不能同时成立

B．若事件 $ A $ ， $ B $ ， $ C $ 两两独立，则 $ P(ABC)=P(A)P(B)P(C) $

C．互斥的事件一定是对立事件，对立事件不一定是互斥事件

D．事件 $ A $ 与事件 $ B $ 中至少有一个发生的概率一定比 $ A $ 与 $ B $ 中恰有一个发生的概率大

答案：A

解析：

因为 $ P(A) > 0 $ , $ P(B) > 0 $ ,若事件 $ A $ , $ B $ 相互独立,则 $ P(AB)=P(A)P(B) > 0 $ ,故事件 $ A $ , $ B $ 不互斥；若事件 $ A $ , $ B $ 互斥,则 $ P(AB)=0 $ , $ P(AB)\ne P(A)P(B) $ ,故事件 $ A $ , $ B $ 不独立,故 $ \mathrm{A} $ 正确.

三个事件 $ A $ , $ B $ , $ C $ 两两独立能推出 $ P(AB)=P(A)\cdot P(B) $ , $ P(AC)=P(A)P(C) $ , $ P(BC)=P(B)P(C) $ ,但是推不出 $ P(ABC)=P(A)P(B)P(C) $ ,比如,从1,2,3,4中随机选出一个数字,事件 $ A： $ 取出的数字为1或2,事件 $ B： $ 取出的数字为1或3,事件 $ C： $ 取出的数字为1或4,则事件 $ AB=AC=BC=ABC： $ 取出的数字为1,所以 $ P(A)=P(B)=P(C)=\dfrac{1}{2} $ , $ P(AB)=P(AC)=P(BC)=P(ABC)=\dfrac{1}{4} $ ,满足 $ P(AB)=P(A)P(B) $ , $ P(AC)=P(A)P(C) $ , $ P(BC)=P(B)P(C) $ ,

所以事件 $ A $ , $ B $ , $ C $ 两两独立,

但是推不出 $ P(ABC)=P(A)P(B)P(C) $ ,故 $ \mathrm{B} $ 错误.

互斥的事件不一定是对立事件,对立事件一定是互斥事件,故 $ \mathrm{C} $ 错误.

当事件 $ A $ 与事件 $ B $ 为对立事件时,事件 $ A $ 与事件 $ B $ 中至少有一个发生的概率和 $ A $ 与 $ B $ 中恰有一个发生的概率相等,故 $ \mathrm{D} $ 错误.

7．下列对各事件发生的概率判断正确的是（）

①某学生在上学的路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是 $ \dfrac{1}{3} $ ，那么该学生在上学路上到第3个路口首次遇到红灯的概率为 $ \dfrac{4}{27} $ ；

②三人独立地破译一份密码，他们能单独译出的概率分别为 $ \dfrac{1}{5} $ ， $ \dfrac{1}{3} $ ， $ \dfrac{1}{4} $ ，假设他们破译密码是彼此独立的，则此密码被破译的概率为 $ \dfrac{2}{5} $ ；

③甲袋中有8个白球，4个红球，乙袋中有6个白球，6个红球，从每个袋中任取一个球，则取到同色球的概率为 $ \dfrac{1}{2} $ ；

④设两个独立事件 $ A $ 和 $ B $ 都不发生的概率为 $ \dfrac{1}{9} $ ， $ A $ 发生 $ B $ 不发生的概率与 $ B $ 发生 $ A $ 不发生的概率相同，则事件 $ A $ 发生的概率是 $ \dfrac{2}{9} $ .

A．①③

B．①④

C．①②③

D．①③④

答案：A

解析：

对于①,记事件 $ {A}_{i}(i=1,2,3,4) $ 表示第 $ i $ 个路口遇到红灯,

则该学生在上学路上到第3个路口首次遇到红灯的概率为 $ P({\overline{A}}_{1}{\overline{A}}_{2}{A}_{3})=P(\overline{{A}_{1}})\cdot P(\overline{{A}_{2}})P({A}_{3})=\dfrac{2}{3}×\dfrac{2}{3}×\dfrac{1}{3}=\dfrac{4}{27} $ ,所以①正确；

对于②,由题知此密码被破译的概率为 $ P=1-(1-\dfrac{1}{5})(1-\dfrac{1}{3})(1-\dfrac{1}{4})=\dfrac{3}{5} $ ,所以②错误；

对于③,因为从甲袋中任取一个球,取到红球的概率为 $ \dfrac{4}{8+4}=\dfrac{1}{3} $ ,取到白球的概率为 $ 1-\dfrac{1}{3}=\dfrac{2}{3} $ ,从乙袋中任取一个球,取到红球的概率为 $ \dfrac{6}{6+6}=\dfrac{1}{2} $ ,取到白球的概率为 $ 1-\dfrac{1}{2}=\dfrac{1}{2} $ ,所以从每个袋中任取一个球,则取到同色球的概率为 $ P=\dfrac{1}{3}×\dfrac{1}{2}+\dfrac{2}{3}×\dfrac{1}{2}=\dfrac{1}{2} $ ,故③正确；

对于④,设事件 $ A $ 和 $ B $ 发生的概率分别为 $ {p}_{1} $ , $ {p}_{2} $ ,又事件 $ A $ 和 $ B $ 相互独立,

由题知 $ \begin{cases}P(\overline{A}\overline{B})=\dfrac{1}{9},\\ P(\overline{A}B)=P(A\overline{B}),\end{cases} $

即 $ \begin{cases}(1-{p}_{1})(1-{p}_{2})=\dfrac{1}{9},\\ (1-{p}_{1}){p}_{2}={p}_{1}(1-{p}_{2}),\end{cases} $ 解得 $ {p}_{1}=\dfrac{2}{3} $ ,所以④错误.

故选 $ \mathrm{A} $ .

8．甲、乙、丙三人进行传球游戏，每次抛掷一枚质地均匀的正方体骰子决定传球的方式，当球在甲手中时，若骰子点数大于3，则甲将球传给乙，若点数不大于3，则甲将球保留；当球在乙手中时，若骰子点数大于4，则乙将球传给甲，若点数不大于4，则乙将球传给丙；当球在丙手中时，若骰子点数大于3，则丙将球传给甲，若点数不大于3，则丙将球传给乙.初始时，球在甲手中，抛掷3次骰子后，球在甲手中的概率为（）

A． $ \dfrac{1}{8} $

B． $ \dfrac{1}{3} $

C． $ \dfrac{5}{24} $

D． $ \dfrac{11}{24} $

答案：D

解析：

由题意,当抛掷3次骰子后,球在甲手中,共有4种情况：

①甲 $ \to $ 甲 $ \to $ 甲 $ \to $ 甲,概率为 $ \dfrac{1}{2}×\dfrac{1}{2}×\dfrac{1}{2}=\dfrac{1}{8} $ ；

②甲 $ \to $ 甲 $ \to $ 乙 $ \to $ 甲,概率为 $ \dfrac{1}{2}×\dfrac{1}{2}×\dfrac{1}{3}=\dfrac{1}{12} $ ；

③甲 $ \to $ 乙 $ \to $ 甲 $ \to $ 甲,概率为 $ \dfrac{1}{2}×\dfrac{1}{3}×\dfrac{1}{2}=\dfrac{1}{12} $ ；

④甲 $ \to $ 乙 $ \to $ 丙 $ \to $ 甲,概率为 $ \dfrac{1}{2}×\dfrac{2}{3}×\dfrac{1}{2}=\dfrac{1}{6} $ .

所以抛掷3次骰子后,球在甲手中的概率 $ P=\dfrac{1}{8}+\dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{6}=\dfrac{11}{24} $ .故选 $ \mathrm{D} $ .

9．已知 $ A $ ， $ B $ 为随机事件， $ P(A)=0.5 $ ， $ P(B)=0.3 $ ，下列结论正确的有（）（多选）

A．若 $ A $ ， $ B $ 为互斥事件，则 $ P(A\cup B)=0.8 $

B．若 $ A $ ， $ B $ 为互斥事件，则 $ P(\overline{A}\cup \overline{B})=0.2 $

C．若 $ A $ ， $ B $ 相互独立，则 $ P(A\cup B)=0.65 $

D．若 $ A $ ， $ B $ 相互独立，则 $ P(\overline{A}B\cup A\overline{B})=0.5 $

答案：ACD

解析：

对于 $ \mathrm{A} $ , $ \mathrm{B} $ ,因为 $ A $ , $ B $ 为互斥事件,所以 $ P(AB)=0 $ ,

所以 $ P(A\cup B)=P(A)+P(B)-P(AB)=0.8 $ , $ P(\overline{A}\cup \overline{B})=P(\overline{A})+P(\overline{B})-P(\overline{A}\overline{B})=P(\overline{A})+P(\overline{B})-[P(\overline{B})-P(A)]=1.2-0.2=1 $ ,所以 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误；

对于 $ \mathrm{C} $ , $ \mathrm{D} $ ,因为 $ A $ , $ B $ 相互独立,所以 $ P(AB)=P(A)P(B)=0.15 $ ,所以 $ P(A\cup B)=P(A)+P(B)-P(AB)=0.65 $ , $ P(\overline{A}B\cup A\overline{B})=P(\overline{A}B)+P(A\overline{B})-0=P(\overline{A})P(B)+P(A)P(\overline{B})=0.5 $ ,所以 $ \mathrm{C} $ , $ \mathrm{D} $ 正确.

故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .

10．在一个不透明的袋子中，装有大小、材质相同的2个红球和3个绿球，从袋中依次抽取2个球，记 $ {R}_{i}= $ “第 $ i $ 次取到红球”， $ {G}_{i}= $ “第 $ i $ 次取到绿球”，其中 $ i=1 {\rm ,2} $ ，下列说法正确的是（）（多选）

A．若有放回地抽取，则 $ P({R}_{1})=P({R}_{2})=P({G}_{1})=P({G}_{2})=\dfrac{1}{5} $

B．若有放回地抽取，则 $ P({R}_{1}{G}_{2})=\dfrac{6}{25} $

C．若不放回地抽取，则 $ P({R}_{1}{G}_{2})=\dfrac{3}{10} $

D．若不放回地抽取，则 $ P({R}_{1}+{G}_{2})=\dfrac{7}{10} $

答案：BCD

解析：

给大小、材质相同的2个红球编号为 $ a $ , $ b {\rm ,3} $ 个绿球编号为 $ c $ , $ d $ , $ e $ ,

若有放回地抽取,则样本空间 $ \mathrm{\Omega }=｛(x,y)|x $ , $ y\in ｛a $ , $ b $ , $ c $ , $ d $ , $ e｝｝ $ ,共包含25个样本点,

其中第一次摸到红球,有 $ ｛(x,y)|x\in ｛a $ , $ b｝ $ , $ y\in ｛a $ , $ b $ , $ c $ , $ d $ , $ e｝｝ $ ,包含10个样本点,

第二次摸到红球,有 $ ｛(x,y)|x\in ｛a $ , $ b $ , $ c $ , $ d $ , $ e｝ $ , $ y\in ｛a $ , $ b｝｝ $ ,包含10个样本点,

第一次摸到绿球,有 $ ｛(x,y)|x\in ｛c $ , $ d $ , $ e｝ $ , $ y\in ｛a $ , $ b $ , $ c $ , $ d $ , $ e｝｝ $ ,包含15个样本点,

第二次摸到绿球,有 $ ｛(x,y)|x\in ｛a $ , $ b $ , $ c $ , $ d $ , $ e｝ $ , $ y\in ｛c $ , $ d $ , $ e｝｝ $ ,包含15个样本点,

所以 $ P({R}_{1})=P({R}_{2})=\dfrac{10}{25}=\dfrac{2}{5} $ , $ P({G}_{1})=P({G}_{2})=\dfrac{15}{25}=\dfrac{3}{5} $ ,故 $ \mathrm{A} $ 错误；

因为事件 $ {R}_{1}{G}_{2}=｛(x,y)|x\in ｛a $ , $ b｝ $ , $ y\in ｛c $ , $ d $ , $ e｝｝ $ ,包含6个样本点,

所以 $ P({R}_{1}{G}_{2})=\dfrac{6}{25} $ ,故 $ \mathrm{B} $ 正确；

若不放回地抽取,则样本空间 $ {\mathrm{\Omega }}_{1}=｛ab $ , $ ac $ , $ ad $ , $ ae $ , $ ba $ , $ bc $ , $ bd $ , $ be $ , $ ca $ , $ cb $ , $ cd $ , $ ce $ , $ da $ , $ db $ , $ dc $ , $ de $ , $ ea $ , $ eb $ , $ ec $ , $ ed｝ $ ,共含有20个样本点,因为事件 $ {R}_{1}{G}_{2}=｛ac $ , $ ad $ , $ ae $ , $ bc $ , $ bd $ , $ be｝ $ ,其中包含6个样本点,所以 $ P({R}_{1}{G}_{2})=\dfrac{6}{20}=\dfrac{3}{10} $ ,故 $ \mathrm{C} $ 正确；因为事件 $ {R}_{1}+{G}_{2}=｛ab $ , $ ac $ , $ ad $ , $ ae $ , $ ba $ , $ bc $ , $ bd $ , $ be $ , $ cd $ , $ ce $ , $ dc $ , $ de $ , $ ec $ , $ ed｝ $ ,其中包含14个样本点,所以 $ P({R}_{1}+{G}_{2})=\dfrac{14}{20}=\dfrac{7}{10} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .

11．某青少年篮球训练营在一堂训练课结束后，组织学员进行投篮测试，规则为

①每人最多投篮3次，先在三分线外投第一次，投中得3分，不中不得分；

②从第二次开始均在三分线内罚球线附近投篮，投中得2分，不中不得分；

③测试者累计得分超过3分即通过测试，并立即终止，累计得分不超过3分则继续投篮.

已知学员小明参加测试，他一次投篮得3分和2分的概率分别为0.2和 $ 0.6 $ ，各次投篮是否投中互不影响，则（）（多选）

A．小明测试得3分的概率为0.032

B．小明测试得5分的概率为0.168

C．小明测试一共投篮3次的概率为0.336

D．小明测试通过的概率为0.456

答案：ABD

解析：

设小明第一次投篮投中为事件 $ A $ ,第二次投篮投中为事件 $ B $ ,第三次投篮投中为事件 $ C $ ,

则 $ P(A)=0.2 $ , $ P(B)=0.6 $ , $ P(C)=0.6 $ .

对于 $ \mathrm{A} $ ：小明测试得3分为事件 $ A\overline{B}\overline{C} $ ,

则 $ P(A\overline{B}\overline{C})=P(A)P(\overline{B})P(\overline{C})=0.2×(1-0.6)×(1-0.6)=0.032 $ ,故 $ \mathrm{A} $ 正确.

对于 $ \mathrm{B} $ ：小明测试得5分为事件 $ A\overline{B}C\cup AB $ ,

则 $ P(A\overline{B}C\cup AB)=P(A\overline{B}C)+P(AB)=P(A)P(\overline{B})P(C)+P(A)P(B)=0.2×0.4×0.6+0.2×0.6=0.168 $ ,故 $ \mathrm{B} $ 正确.

对于 $ \mathrm{C} $ ：小明测试一共投篮3次为事件 $ A\overline{B}\cup \overline{A}B\cup \overline{A}\overline{B} $ ,则 $ P(A\overline{B}\cup \overline{A}B\cup \overline{A}\overline{B})=P(A\overline{B})+P(\overline{A}B)+P(\overline{A}\overline{B})=P(A)P(\overline{B})+P(\overline{A})P(B)+P(\overline{A})P(\overline{B})=0.2×0.4+0.8×0.6+0.8×0.4=0.88 $ ,故 $ \mathrm{C} $ 错误.

对于 $ \mathrm{D} $ ：小明测试通过为事件 $ AB\cup \overline{A}BC\cup A\overline{B}C $ , $ P(AB\cup \overline{A}BC\cup A\overline{B}C)=P(AB)+P(\overline{A}BC)+P(A\overline{B}C)=P(A)P(B)+P(\overline{A})P(B)P(C)+P(A)P(\overline{B})P(C)=0.2×0.6+0.8×0.6×0.6+0.2×0.4×0.6=0.456 $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .

13．某保险柜的密码由0，1，2，3，4，5，6，7，8，9中的四个数字组成，假设一个人记不清自己的保险柜密码，只记得密码全部由奇数组成且按照递增顺序排列，则最多输入2次就能打开保险柜的概率是 .

答案：

$ \dfrac{2}{5} $

解析：

密码全部由奇数组成且按照递增顺序排列的结果有 $ (1,3,5,7) $ , $ (1,3,5,9) $ , $ (1,3,7,9) $ , $ (1,5,7,9) $ , $ (3,5,7,9) $ ,共5个.

设最多输入2次就能打开保险柜为事件 $ A $ ,输入1次能打开保险柜为事件 $ {A}_{1} $ ,第2次输入才能打开保险柜为事件 $ {A}_{2} $ ,则 $ A={A}_{1}+{A}_{2} $ 且 $ {A}_{1} $ , $ {A}_{2} $ 互斥,

由题意知 $ P({A}_{1})=\dfrac{1}{5} $ , $ P({A}_{2})=\dfrac{4}{5}×\dfrac{1}{4}=\dfrac{1}{5} $ ,则 $ P(A)=P({A}_{1})+P({A}_{2})=\dfrac{2}{5} $ ,

所以最多输入2次就能打开保险柜的概率是 $ \dfrac{2}{5} $ .

14．甲、乙、丙、丁四支球队进行单循环小组赛，比赛分三轮，每轮两场比赛，具体赛程如表：

第一轮	甲 $ \mathrm{V}\mathrm{S} $ 乙	丙 $ \mathrm{V}\mathrm{S} $ 丁
第二轮	甲 $ \mathrm{V}\mathrm{S} $ 丙	乙 $ \mathrm{V}\mathrm{S} $ 丁
第三轮	甲 $ \mathrm{V}\mathrm{S} $ 丁	乙 $ \mathrm{V}\mathrm{S} $ 丙

规定：每场比赛获胜的球队记3分，输的球队记0分，平局两队各记1分，三轮比赛结束后以总分排名.总分相同的球队以抽签的方式确定排名，排名前两位的球队出线.假设甲、乙、丙三支球队水平相当，彼此间胜、负、平的概率均为 $ \dfrac{1}{3} $ ，丁的水平较弱，面对其他任意一支球队胜、负、平的概率都分别为 $ \dfrac{1}{6} $ ， $ \dfrac{1}{2} $ ， $ \dfrac{1}{3} $ .每场比赛结果相互独立.

（1）丁的总分为7分的概率为；

（2）若第一轮比赛结束，甲、乙、丙、丁四支球队积分分别为3，0，3，0，则丁以6分的成绩出线的概率为 .（答对一空给3分）

答案：

（1） $ \dfrac{1}{36} $

（2） $ \dfrac{13}{486} $

解析：

（1）记第 $ i $ 轮比赛丁胜、平、负的事件分别为 $ {A}_{i} $ , $ {B}_{i} $ , $ {C}_{i}(i=1,2,3) $ ,每场比赛结果相互独立.丁总分为7分,则丁三场比赛两胜一平,记丁三轮比赛两胜一平的事件为 $ D $ ,

所以 $ P(D)=P({A}_{1}{A}_{2}{B}_{3})+P({A}_{1}{B}_{2}{A}_{3})+P({B}_{1}{A}_{2}{A}_{3})=3×{\left(\dfrac{1}{6}\right) ^ {2}}×\dfrac{1}{3}=\dfrac{1}{36} $ .

（2）由题意知第一轮比赛,甲胜乙,丙胜丁,又丁总分为6分,则丁对战甲、乙都获胜,

此时乙队总分最多3分,少于丁队总分.

①第二轮中若甲负于丙或平丙时,甲总分最多4分,少于丁队总分,

此时甲、乙两队少于丁队总分,丁一定出线,

其相应的概率为 $ {P}_{1}=(\dfrac{1}{3}+\dfrac{1}{3})×\dfrac{1}{6}×\dfrac{1}{6}=\dfrac{1}{54} $ ；

②第二轮中若甲胜丙、第三轮中丙平乙或负于乙时,丙总分最多4分,

此时丙、乙两队少于丁队总分,丁一定出线,其相应的概率为 $ {P}_{2}=\dfrac{1}{3}×\dfrac{1}{6}×(\dfrac{1}{3}+\dfrac{1}{3})×\dfrac{1}{6}=\dfrac{1}{162} $ ；

③第二轮中若甲胜丙、第三轮中丙胜乙时,甲、丁、丙队总分均为6分,此时由抽签确定出线,三队中有两队出线,每队出线概率均为 $ \dfrac{2}{3} $ ,丁队出线的概率为 $ {P}_{3}=\dfrac{1}{3}×\dfrac{1}{6}×\dfrac{1}{3}×\dfrac{1}{6}×\dfrac{2}{3}=\dfrac{1}{486} $ .

综上,丁以6分的成绩出线的概率为 $ {P}_{1}+{P}_{2}+{P}_{3}=\dfrac{1}{54}+\dfrac{1}{162}+\dfrac{1}{486}=\dfrac{13}{486} $ .

15．（本小题满分13分）某班统计出某天学生向老师咨询物理、化学、生物问题的数量，其中咨询的物理问题有30道，化学问题有20道，生物问题有10道.现从当天咨询的所有问题中用按比例分配的分层随机抽样的方法抽取样本容量为6的样本，再从样本中一次性任取2题.

（1）从样本中任取2题的样本点用 $ (x,y) $ 的形式表示，写出所有的样本点；

（2）求任取的2题中恰好有物理和化学问题各1道的概率.

答案：

（1）【解】用按比例分配的分层随机抽样抽到物理、化学、生物问题的数量分别为 $ \dfrac{30}{60}×6=3 $ , $ \dfrac{20}{60}×6=2 $ , $ \dfrac{10}{60}×6=1 $ .

不妨令抽到的3个物理问题为 $ {a}_{1} $ , $ {a}_{2} $ , $ {a}_{3} {\rm ,2} $ 个化学问题为 $ {b}_{1} $ , $ {b}_{2} {\rm ,1} $ 个生物问题为 $ c $ .

若从样本中任取2题,有 $ ({a}_{1},{a}_{2}) $ , $ ({a}_{1},{a}_{3}) $ , $ ({a}_{1},{b}_{1}) $ , $ ({a}_{1},{b}_{2}) $ , $ ({a}_{1},c) $ , $ ({a}_{2},{a}_{3}) $ , $ ({a}_{2},{b}_{1}) $ , $ ({a}_{2},{b}_{2}) $ , $ ({a}_{2},c) $ , $ ({a}_{3},{b}_{1}) $ , $ ({a}_{3},{b}_{2}) $ , $ ({a}_{3},c) $ , $ ({b}_{1},{b}_{2}) $ , $ ({b}_{1},c) $ , $ ({b}_{2},c) $ ,共15个样本点.

（2）由（1）知,恰好抽到物理和化学问题各1道的样本点共有6个,所以恰好抽到物理和化学问题各1道的概率为 $ \dfrac{6}{15}=\dfrac{2}{5} $ .

解析：

16．（本小题满分15分）在甲、乙两个盒子中分别装有标号为1，2，3，4的4个大小、质地相同的球，现从甲、乙两个盒子中各取出1个球，每个球被取出的可能性相等.

（1）列出所有的可能结果；设取出的两个球上的标号为相同数字为事件 $ A $ ，写出事件 $ A $ 包含的样本点集合，并求出事件 $ A $ 发生的概率 $ P(A) $ .

（2）设取出的两个球上标号之积能被3整除为事件 $ B $ ，求事件 $ B $ 发生的概率 $ P(B) $ .

答案：

（1）【解】由题意,设从甲、乙两个盒子中各取出1个球,其数字分别为 $ x $ , $ y $ ,用 $ (x,y) $ 表示抽取结果,

可得 $ (1,1) $ , $ (1,2) $ , $ (1,3) $ , $ (1,4) $ , $ (2,1) $ , $ (2,2) $ , $ (2,3) $ , $ (2,4) $ , $ (3,1) $ , $ (3,2) $ , $ (3,3) $ , $ (3,4) $ , $ (4,1) $ , $ (4,2) $ , $ (4,3) $ , $ (4,4) $ ,

则所有的样本点有16个.

其中 $ A=｛(1,1) $ , $ (2,2) $ , $ (3,3) $ , $ (4,4)｝ $ ,共4个样本点,

故取出的两个球上的标号为相同数字的概率 $ P(A)=\dfrac{4}{16}=\dfrac{1}{4} $ .

（2）由题意可得, $ B=｛(1,3) $ , $ (3,1) $ , $ (2,3) $ , $ (3,2) $ , $ (3,3) $ , $ (3,4) $ , $ (4,3)｝ $ ,共7个样本点,

故取出的两个球上标号之积能被3整除的概率 $ P(B)=\dfrac{7}{16} $ .

解析：

17．（本小题满分15分）某高校“强基计划”自主招生的面试中有三道不同的题目，每位面试者依次作答.若答对两道题目，则面试通过，结束面试；若答错两道题目，则面试不通过，结束面试.已知李明答对第一道题目的概率为 $ \dfrac{4}{5} $ ，答对第二道题目的概率为 $ \dfrac{3}{5} $ ，答对第三道题目的概率为 $ \dfrac{2}{5} $ ，假设每道题目是否答对是独立的.

（1）求李明答完第二道题后结束面试的概率；

（2）求李明最终通过面试的概率.

答案：

（1）【解】设 $ {A}_{i} $ 表示“李明答对第 $ {\rm }{\rm i}({\rm i}=1,2,3) $ 道题目”, $ B $ 表示“李明答完第二道题后结束面试”,则 $ B={A}_{1}{A}_{2}\cup \overline{{A}_{1}}\overline{{A}_{2}}{\rm } $ ,且 $ {A}_{1}{A}_{2} $ , $ \overline{{A}_{1}}\overline{{A}_{2}} $ 互斥.因为每道题目是否答对是独立的,所以 $ {A}_{1} $ 与 $ {A}_{2} $ 相互独立, $ \overline{{A}_{1}} $ 与 $ \overline{{A}_{2}} $ 相互独立,于是 $ P(B)=P({A}_{1}{A}_{2}\cup \overline{{A}_{1}}\overline{{A}_{2}})=P({A}_{1}{A}_{2})+P(\overline{{A}_{1}}\overline{{A}_{2}})=P({A}_{1})P({A}_{2})+P(\overline{{A}_{1}})P(\overline{{A}_{2}})=\dfrac{4}{5}×\dfrac{3}{5}+\dfrac{1}{5}×\dfrac{2}{5}=\dfrac{14}{25} $ .

（2）设 $ C $ 表示“李明最终通过面试”,则 $ C={A}_{1}{A}_{2}\cup {A}_{1}\overline{{A}_{2}}{A}_{3}\cup \overline{{A}_{1}}{A}_{2}{A}_{3} $ 且 $ {A}_{1}{A}_{2} $ , $ {A}_{1}\overline{{A}_{2}}{A}_{3} $ , $ \overline{{A}_{1}}{A}_{2}{A}_{3} $ 互斥,

所以 $ P(C)=P({A}_{1}{A}_{2}\cup {A}_{1}\overline{{A}_{2}}{A}_{3}\cup \overline{{A}_{1}}{A}_{2}{A}_{3})=P({A}_{1}{A}_{2})+P({A}_{1}\overline{{A}_{2}}{A}_{3})+P(\overline{{A}_{1}}{A}_{2}{A}_{3}) $

$ =P({A}_{1})P({A}_{2})+P({A}_{1})P(\overline{{A}_{2}})P({A}_{3})+P(\overline{{A}_{1}})P({A}_{2})P({A}_{3})=\dfrac{4}{5}×\dfrac{3}{5}+\dfrac{4}{5}×\dfrac{2}{5}×\dfrac{2}{5}+\dfrac{1}{5}×\dfrac{3}{5}×\dfrac{2}{5}=\dfrac{82}{125} $ .

解析：

18．（本小题满分17分）我国水资源的状况不容乐观，某政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准 $ x $ （吨），一位居民的月用水量不超过 $ x $ 的部分按平价收费，超出 $ x $ 的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照 $ [0,0.5) $ , $ [0.5,1) $ , $ \cdots $ , $ [4,4.5] $ 分成9组，制成了如图所示的频率分布直方图.

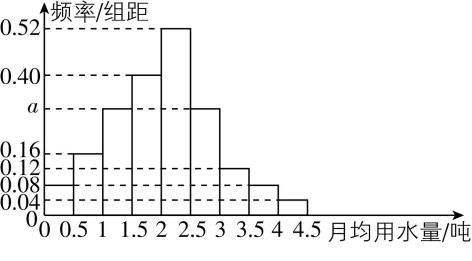
试题资源网 https://stzy.com

（1）求直方图中 $ a $ 的值（保留两位小数）以及估计该地区月均用水量的 $ 60\% $ 分位数；

（2）现在该地区居民中任选2位居民，将月均用水量落入各组的频率视为概率，不同居民的月均用水量相互独立，求恰有1位居民月均用水量大于 $ 60\% $ 分位数的概率；

（3）现有4位居民甲、乙、丙、丁，经调查，甲和乙月均用水量大于 $ 60\% $ 分位数，丙和丁月均用水量不大于 $ 60\% $ 分位数，现从该4人中随机选2人，求所选2人中恰有1人月均用水量大于 $ 60\% $ 分位数的概率.

答案：

（1）【解】由频率分布直方图,得 $ 0.5×(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)=1 $ ,解得 $ a=0.30 $ .

数据落在区间 $ [0,2) $ 内的频率为 $ 0.5×(0.08+0.16+0.30+0.40)=0.47 $ ,

数据落在区间 $ [0,2.5) $ 内的频率为 $ 0.47+0.5×0.52=0.73 $ ,则月均用水量的 $ 60\% $ 分位数 $ m\in [2,2.5) $ ,

由 $ (m-2)×0.52=0.6-0.47 $ ,解得 $ m=2.25 $ .

所以 $ a=0.30 $ ,估计该地区月均用水量的 $ 60\% $ 分位数为2.25.

（2）设事件 $ {A}_{i}(i=1,2) $ 表示第 $ i $ 位居民月均用水量大于 $ 60\% $ 分位数, $ P({A}_{i})=0.4 $ ,

事件 $ B $ 表示恰有1位居民月均用水量大于 $ 60\% $ 分位数, $ B={A}_{1}\overline{{A}_{2}}+\overline{{A}_{1}}{A}_{2} $ ,

因此 $ P(B)=P({A}_{1}\overline{{A}_{2}})+P(\overline{{A}_{1}}{A}_{2})=0.4×0.6+0.6×0.4=0.48 $ ,

所以所求概率为0.48.

（3）样本空间 $ \mathrm{\Omega }=｛ $ （甲,乙）,（甲,丙）,（甲,丁）,（乙,丙）,（乙,丁）,（丙,丁）},共6个样本点,事件 $ D $ 表示所选2人中恰有1人月均用水量大于 $ 60\% $ 分位数,

则 $ D=｛ $ （甲,丙）,（甲,丁）,（乙,丙）,（乙,丁）},共4个样本点,

所以 $ P(D)=\dfrac{4}{6}=\dfrac{2}{3} $ .

解析：

19．（本小题满分17分）甲、乙两支篮球队进入某次决赛，比赛采用“主客场比赛制”，具体赛制如下：若某队两场比赛均获胜或一胜一平，则获得冠军；若某队两场比赛均平局或一胜一负，则通过加时赛决出冠军.现假定甲队在主场获胜的概率为 $ p $ ，平局的概率为 $ \dfrac{2p}{3} $ ，其中 $ 0 < p < 1 $ ；甲队在客场获胜和平局的概率均为 $ \dfrac{p}{2} $ ；加时赛甲队获胜的概率为 $ p $ .不同场对阵的结果相互独立，假设甲队先主场后客场.

（1）已知 $ p=\dfrac{2}{5} $ .

$ {\rm （i）} $ 求甲队通过加时赛获得冠军的概率；

$ {\rm （ii）} $ 求甲队获得冠军的概率.

（2）除“主客场比赛制”外，也经常采用在第三方场地的“单场比赛制”：若某队比赛获胜则获得冠军；若为平局，则通过加时赛决出冠军.假定甲队在第三方场地获胜的概率为 $ {p}^{2} $ ，平局的概率为 $ \dfrac{p}{2} $ ，加时赛甲队获胜的概率为 $ p $ .问哪种赛制更有利于甲队夺冠？

答案：

$ {\rm （i）} $ 【解】设甲队通过加时赛获得冠军为事件 $ A $ ,

则事件 $ A $ 包含甲队主胜客负,主负客胜,主平客平,然后加时赛获胜,

所以 $ P(A)=[p(1-p)+(1-\dfrac{5p}{3})\dfrac{p}{2}+\dfrac{2p}{3}\cdot \dfrac{p}{2}]p=\dfrac{3{p}^{2}(1-p)}{2} $ .

因为 $ p=\dfrac{2}{5} $ ,所以 $ P(A)=\dfrac{3×{\left(\dfrac{2}{5}\right) ^ {2}}×(1-\dfrac{2}{5})}{2}=\dfrac{18}{125} $ .

$ {\rm （ii）} $ 设甲队获得冠军为事件 $ B $ ,

则事件 $ B $ 包含甲队加时赛胜,主胜客胜,主胜客平,主平客胜,

则 $ P(B)=P(A)+p\cdot \dfrac{p}{2}+p\cdot \dfrac{p}{2}+\dfrac{2p}{3}\cdot \dfrac{p}{2}=\dfrac{17{p}^{2}}{6}-\dfrac{3{p}^{3}}{2} $ .

因为 $ p=\dfrac{2}{5} $ ,所以 $ P(B)=\dfrac{17}{6}×{\left(\dfrac{2}{5}\right) ^ {2}}-\dfrac{3}{2}×{\left(\dfrac{2}{5}\right) ^ {3}}=\dfrac{134}{375} $ .

（2）在第三方场地的“单场比赛制”下,将甲队获胜记为事件 $ C $ ,

则事件 $ C $ 包含甲队胜,甲队平且加时赛胜,

则 $ P(C)={p}^{2}+\dfrac{1}{2}p\cdot p=\dfrac{3{p}^{2}}{2} $ ,

因为 $ 0 < p+\dfrac{2p}{3} < 1 $ ,所以 $ 0 < p < \dfrac{3}{5} $ ,此时 $ 0 < {p}^{2}+\dfrac{p}{2} < \dfrac{33}{50} $ ,符合题意,

$ P(B)-P(C)=\dfrac{17{p}^{2}}{6}-\dfrac{3{p}^{3}}{2}-\dfrac{3{p}^{2}}{2}=\dfrac{4{p}^{2}}{3}-\dfrac{3{p}^{3}}{2}=\dfrac{{p}^{2}}{6}(8-9p) $ .

因为 $ 0 < p < \dfrac{3}{5} $ , $ \dfrac{{p}^{2}}{6} > 0 $ , $ 8-9p > 0 $ ,

所以 $ P(B)-P(C) > 0 $ ,即 $ P(B) > P(C) $ ,

所以“主客场比赛制”比第三方场地的“单场比赛制”更有利于甲队夺冠.

解析：

第十章素养检测

一、刷速度