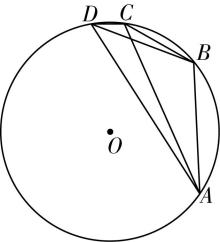
4.克罗狄斯·托勒密是希腊数学家,他博学多才,既是天文学权威,也是地理学大师.托勒密定理是平面几何中非常著名的定理,它揭示了圆内接四边形的对角线与边长的内在联系,该定理的内容为圆的内接四边形中,两对角线长的乘积等于两组对边长乘积之和.已知四边形 $ ABCD $ 是圆 $ O $ 的内接四边形,且 $ AC=\sqrt{3}BD $ , $ \mathrm{\angle }ADC=2\mathrm{\angle }BAD. $ 若 $ AB\cdot CD+BC\cdot AD=4\sqrt{3} $ ,则圆 $ O $ 的半径为 .
2
由托勒密定理,得 $ AC\cdot BD=AB\cdot CD+BC\cdot AD=4\sqrt{3} $ .
因为 $ AC=\sqrt{3}BD $ ,所以 $ BD=2 $ .设圆 $ O $ 的半径为 $ R $ ,由正弦定理,得 $ \dfrac{AC}{ \sin \mathrm{\angle }ADC}=\dfrac{BD}{ \sin \mathrm{\angle }BAD}=2R $ .
又 $ AC=\sqrt{3}BD $ ,所以 $ \sin \mathrm{\angle }ADC=\sqrt{3} \sin \mathrm{\angle }BAD $ .
因为 $ \mathrm{\angle }ADC=2\mathrm{\angle }BAD $ ,所以 $ 2 \sin \mathrm{\angle }BAD\cdot \cos \mathrm{\angle }BAD=\sqrt{3} \sin \mathrm{\angle }BAD $ .
因为 $ 0 < \mathrm{\angle }BAD < \mathrm{\pi } $ ,所以 $ \sin \mathrm{\angle }BAD > 0 $ ,所以 $ \cos \mathrm{\angle }BAD=\dfrac{\sqrt{3}}{2} $ ,所以 $ \sin \mathrm{\angle }BAD=\sqrt{1-{ \cos }^{2}\mathrm{\angle }BAD}=\dfrac{1}{2} $ ,所以 $ 2R=\dfrac{BD}{ \sin \mathrm{\angle }BAD}=4 $ ,故 $ R=2 $ .