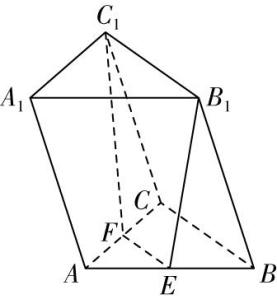
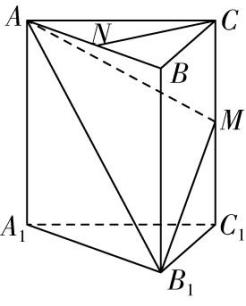
19.空间的弯曲性是几何研究的重要内容,用曲率刻画空间的弯曲性,规定:多面体顶点的曲率等于 $ 2\mathrm{\pi } $ 与多面体在该点的面角之和的差,其中多面体的面的内角叫作多面体的面角,角度用弧度制.例如:正四面体每个顶点均有3个面角,每个面角均为 $ \dfrac{\mathrm{\pi }}{3} $ ,故其各个顶点的曲率均为 $ 2\mathrm{\pi }-3×\dfrac{\mathrm{\pi }}{3}=\mathrm{\pi } $ .如图,在直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 中,点 $ A $ 的曲率为 $ \dfrac{2\mathrm{\pi }}{3} $ , $ N $ , $ M $ 分别为 $ AB $ , $ C{C}_{1} $ 的中点,且 $ AB=AC $ .
(1) 证明: $ CN\perp $ 平面 $ AB{B}_{1}{A}_{1} $ .
(2) 若 $ A{A}_{1}=\sqrt{2}AB $ ,求二面角 $ {B}_{1}-AM-{C}_{1} $ 的余弦值.
(3) 表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名的欧拉定理:设简单多面体的顶点数为 $ D $ ,棱数为 $ L $ ,面数为 $ M $ ,则有 $ D-L+M=2 $ .利用此定理试证明:简单多面体的总曲率(多面体所有顶点的曲率之和)是常数.
答案:(1) 【证明】因为在直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 中, $ A{A}_{1}\perp $ 平面 $ ABC $ , $ AC $ , $ AB\subset $ 平面 $ ABC $ ,
所以 $ A{A}_{1}\perp AC $ , $ A{A}_{1}\perp AB $ ,所以点 $ A $ 的曲率为 $ 2\mathrm{\pi }-2×\dfrac{\mathrm{\pi }}{2}-\mathrm{\angle }BAC=\dfrac{2\mathrm{\pi }}{3} $ ,得 $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{3} $ .
又 $ AB=AC $ ,所以 $ △ABC $ 为等边三角形.
因为 $ N $ 为 $ AB $ 的中点,所以 $ CN\perp AB $ .
因为 $ A{A}_{1}\perp $ 平面 $ ABC $ , $ CN\subset $ 平面 $ ABC $ ,
所以 $ A{A}_{1}\perp CN $ .
因为 $ A{A}_{1}\cap AB=A $ , $ A{A}_{1} $ , $ AB\subset $ 平面 $ AB{B}_{1}{A}_{1} $ ,所以 $ CN\perp $ 平面 $ AB{B}_{1}{A}_{1} $ .
(2) 【解】取 $ {A}_{1}{C}_{1} $ 的中点 $ F $ ,连接 $ {B}_{1}F $ , $ MF $ .因为 $ △{A}_{1}{B}_{1}{C}_{1} $ 为等边三角形,
所以 $ {B}_{1}F\perp {A}_{1}{C}_{1} $ .
因为三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 为直三棱柱,
所以平面 $ A{A}_{1}{C}_{1}C\perp $ 平面 $ {A}_{1}{B}_{1}{C}_{1} $ .
因为平面 $ A{A}_{1}{C}_{1}C\cap $ 平面 $ {A}_{1}{B}_{1}{C}_{1}={A}_{1}{C}_{1} $ , $ {B}_{1}F\subset $ 平面 $ {A}_{1}{B}_{1}{C}_{1} $ .
又 $ {B}_{1}F\perp {A}_{1}{C}_{1} $ ,所以 $ {B}_{1}F\perp $ 平面 $ A{A}_{1}{C}_{1}C $ .
因为 $ AM $ , $ MF\subset $ 平面 $ A{A}_{1}{C}_{1}C $ ,
所以 $ {B}_{1}F\perp AM $ , $ {B}_{1}F\perp MF $ ,
故 $ △FM{B}_{1} $ 为直角三角形.
设 $ AB=\sqrt{2} $ ,则 $ A{A}_{1}=2 $ , $ AM={B}_{1}M=\sqrt{3} $ , $ A{B}_{1}=\sqrt{6} $ ,
所以 $ A{M}^{2}+{B}_{1}{M}^{2}=A{B}_{1}^{2} $ ,
所以 $ AM\perp {B}_{1}M $ .
因为 $ {B}_{1}F\cap {B}_{1}M={B}_{1} $ , $ {B}_{1}F $ , $ {B}_{1}M\subset $ 平面 $ {B}_{1}FM $ ,所以 $ AM\perp $ 平面 $ {B}_{1}FM $ .
因为 $ MF\subset $ 平面 $ {B}_{1}FM $ ,所以 $ AM\perp MF $ ,
又 $ AM\perp {B}_{1}M $ ,所以 $ \mathrm{\angle }FM{B}_{1} $ 为二面角 $ {B}_{1}-AM-{C}_{1} $ 的平面角.
因为 $ MF=\sqrt{{\left(\dfrac{\sqrt{2}}{2}\right) ^ {2}}+{1}^{2}}=\dfrac{\sqrt{6}}{2} $ , $ {B}_{1}M=\sqrt{3} $ ,
所以在 $ \mathrm{R}\mathrm{t}△FM{B}_{1} $ 中, $ \cos \mathrm{\angle }FM{B}_{1}=\dfrac{FM}{M{B}_{1}}=\dfrac{\sqrt{2}}{2} $ ,所以二面角 $ {B}_{1}-AM-{C}_{1} $ 的余弦值为 $ \dfrac{\sqrt{2}}{2} $ .

(3) 【证明】设多面体有 $ M $ 个面,给组成多面体的多边形编号,分别为 $ {\rm 1,2,} \cdots $ , $ M $ 号,
设第 $ i $ 号 $ (1\leqslant i\leqslant M) $ 多边形有 $ {L}_{i} $ 条边,
则多面体共有 $ L=\dfrac{{L}_{1}+{L}_{2}+\cdots +{L}_{M}}{2} $ 条棱,
由题意,多面体共有 $ D=2-M+L=2-M+\dfrac{{L}_{1}+{L}_{2}+\cdots +{L}_{M}}{2} $ 个顶点,
第 $ i $ 号多边形的内角之和为 $ \mathrm{\pi }{L}_{i}-2\mathrm{\pi } $ ,
所以多面体的所有多边形的内角之和为 $ \mathrm{\pi }({L}_{1}+{L}_{2}+\cdots +{L}_{M})-2\mathrm{\pi }M $ ,
故多面体的总曲率为
$ 2\mathrm{\pi }D-[\mathrm{\pi }({L}_{1}+{L}_{2}+\cdots +{L}_{M})-2\mathrm{\pi }M] $
$ =2\mathrm{\pi }(2-M+\dfrac{{L}_{1}+{L}_{2}+\cdots +{L}_{M}}{2})-[\mathrm{\pi }({L}_{1}+{L}_{2}+\cdots +{L}_{M})-2\mathrm{\pi }M] $
$ =4\mathrm{\pi } $ ,
所以简单多面体的总曲率为常数 $ 4\mathrm{\pi } $ .
 (多选)
(多选)