课时1 速度 平均速度与瞬时速度
一、刷基础
1.下列关于速度的说法正确的是( )
A. $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ 只适用于直线运动
B.由 $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ 可知, $ v $ 与 $ \mathrm{\Delta }x $ 成正比,与 $ \mathrm{\Delta }t $ 成反比
C.速度不变的运动是匀速运动(非静止)
D.速度的方向与物体位移的方向一致
答案:C
解析: $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ 普遍适用,适用于直线运动,也适用于曲线运动,故 $ \mathrm{A} $ 错误;由 $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ 可知, $ v $ 是由比值定义的物理量, $ v $ 与 $ \mathrm{\Delta }x $ 、 $ \mathrm{\Delta }t $ 的大小没有直接关系,故 $ \mathrm{B} $ 错误;速度是矢量,速度不变即速度大小和方向均不变,所以速度不变的运动是匀速运动(非静止),故 $ \mathrm{C} $ 正确;速度的方向与物体位移的方向不一定相同,故 $ \mathrm{D} $ 错误.
2.小王乘坐由16节车厢编组的高铁旅行.他位于某节车厢尾部,当高铁头部恰好进入隧道时,立即以正常速度向此车厢头部行走.他经过 $ 15\mathrm{s} $ 到达该节车厢头部时,车厢头部恰好出隧道.行走过程中看到车厢内显示屏上的示数一直为 $ 216\mathrm{k}\mathrm{m}/\mathrm{h} $ ,已知每节车厢的长度为 $ 22.5\mathrm{m} $ ,则( )

A.小王相对于车厢的速度大小为 $ 1.5\mathrm{m}/\mathrm{s} $
B.高铁的总长度为 $ 900\mathrm{m} $
C.小王相对于地面所发生的位移大小为 $ 877.5\mathrm{m} $
D.高铁通过隧道的时间为 $ 15\mathrm{s} $
答案:A
解析:每节车厢的长度为 $ x=22.5\mathrm{m} $ ,则小王相对于车厢的速度大小为 $ v=\dfrac{x}{t}=1.5\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 正确;高铁的总长度为 $ s=16x=360\mathrm{m} $ , $ \mathrm{B} $ 错误;高铁相对于地面的速度大小为 $ {v}_{1}=216\mathrm{k}\mathrm{m}/\mathrm{h}=60\mathrm{m}/\mathrm{s} $ ,则小王相对地面的速度大小为 $ v\prime =v+{v}_{1}=61.5\mathrm{m}/\mathrm{s} $ ,小王相对于地面所发生的位移大小为 $ x\prime =v\prime t=922.5\mathrm{m} $ , $ \mathrm{C} $ 错误; 设隧道长度为 $ L $ ,则 $ L=x\prime =922.5\mathrm{m} $ ,列车通过隧道的时间为 $ t\prime =\dfrac{s+L}{{v}_{1}}=21.375\mathrm{s} $ , $ \mathrm{D} $ 错误.
3.关于瞬时速度、平均速度,以下说法中正确的是( )
A.瞬时速度可以看成时间趋于无穷小时的平均速度
B.做变速运动的物体在某段时间内的平均速度大小,一定和物体在这段时间内各个时刻的瞬时速度大小的平均值相等
C.物体做变速直线运动时,平均速度的大小就是平均速率
D.物体做变速运动时,平均速度是指物体通过的路程与所用时间的比值
答案:A
解析:时间趋于无穷小时,物体在这段时间内的运动可以近似看成匀速运动,平均速度等于瞬时速度,故 $ \mathrm{A} $ 正确;做变速运动的物体在某段时间内的平均速度大小等于这段时间内的位移的大小与所用时间的比值,不一定和物体在这段时间内各个时刻的瞬时速度大小的平均值相等,例如绕操场一周回到初始位置,故 $ \mathrm{B} $ 错误;平均速率指总路程与总时间的比值,而平均速度指总位移与总时间的比值,变速直线运动中物体的路程大于等于物体的位移大小,则物体的平均速率大于等于平均速度的大小,故 $ \mathrm{C} $ 错误;做变速运动的物体在某段时间内的平均速度等于位移与发生该段位移所用时间的比值,故 $ \mathrm{D} $ 错误.
4.如图所示,一质点从 $ A $ 点由静止开始运动,经 $ 2\mathrm{s} $ 运动到 $ B $ 点,再经 $ 2\mathrm{s} $ 运动到 $ C $ 点.已知 $ AB=4\mathrm{m} $ , $ BC=10\mathrm{m} $ ,则质点( )

A.在 $ AC $ 段的平均速度大小为 $ 7\mathrm{m}/\mathrm{s} $
B.在 $ BC $ 段的平均速度大小为 $ 5\mathrm{m}/\mathrm{s} $
C.在 $ B $ 点的瞬时速度大小为 $ 4\mathrm{m}/\mathrm{s} $
D.在 $ B $ 点的瞬时速度大小为 $ 3.5\mathrm{m}/\mathrm{s} $
答案:B
解析:质点在 $ AC $ 段的平均速度大小为 $ {\overline{v}}_{AC}=\dfrac{{x}_{AC}}{{t}_{AC}}=3.5\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 错误;在 $ BC $ 段的平均速度大小为 $ {\overline{v}}_{BC}=\dfrac{{x}_{BC}}{{t}_{BC}}=5\mathrm{m}/\mathrm{s} $ , $ \mathrm{B} $ 正确;因质点的运动性质不确定,则 $ B $ 点瞬时速度无法求解, $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
5.对于速度或速率,下列说法中正确的是( )
A.速率是瞬时速度的大小
B.平均速率是平均速度的大小
C.速度是矢量,平均速度是标量
D.平均速度的方向就是物体运动的方向
答案:A
解析:速率是瞬时速度的大小, $ \mathrm{A} $ 正确;平均速率是路程与时间的比值,不是平均速度的大小, $ \mathrm{B} $ 错误;速度和平均速度都是既有大小,又有方向的物理量,均为矢量, $ \mathrm{C} $ 错误;平均速度的方向是位移的方向,不是运动的方向, $ \mathrm{D} $ 错误.
6.扫地机器人因操作简单、使用方便,已逐渐走进了人们的生活.某次清扫过程中,主人在 $ A $ 处启动扫地机器人,在 $ B $ 处完成清扫工作,其规划清扫路线如图所示,完成清扫任务用时 $ 3 \min $ .机器人清扫路线的总长度为 $ 36\mathrm{m} $ , $ A $ 、 $ B $ 两点间的距离为 $ 9\mathrm{m} $ .下列说法正确的是( )
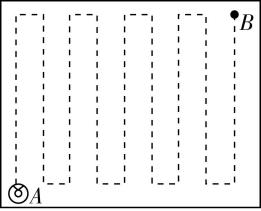
A.机器人在该过程中的位移大小为 $ 36\mathrm{m} $
B.机器人在该过程中的平均速率为 $ 12\mathrm{m}/\mathrm{s} $
C.机器人在该过程中的平均速度大小为 $ 0.05\mathrm{m}/\mathrm{s} $
D.机器人在 $ B $ 点的瞬时速率大小一定为 $ 0.2\mathrm{m}/\mathrm{s} $
答案:C
解析:机器人在该过程中的位移大小为 $ 9\mathrm{m} $ ,路程为 $ 36\mathrm{m} $ , $ \mathrm{A} $ 错误;平均速率等于路程与时间的比值,机器人在该过程中的平均速率为 $ {\overline{v}}_{1}=\dfrac{s}{t}=\dfrac{36}{180}\mathrm{m}/\mathrm{s}=0.2\mathrm{m}/\mathrm{s} $ , $ \mathrm{B} $ 错误;平均速度等于位移与时间的比值,机器人在该过程中的平均速度大小为 $ {\overline{v}}_{2}=\dfrac{x}{t}=\dfrac{9}{180}\mathrm{m}/\mathrm{s}=0.05\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确;题干未明确指出机器人在整个过程中瞬时速率大小不变,故不可认定机器人在 $ B $ 点的瞬时速率等于平均速率 $ 0.2\mathrm{m}/\mathrm{s} $ , $ \mathrm{D} $ 错误.
7.一辆汽车在教练场上沿平直道路行驶,以 $ x $ 表示它相对于出发点的位移,如图近似描绘了汽车在 $ t=0 $ 时刻到 $ t=40\mathrm{s} $ 这段时间内的 $ x-t $ 图像.以下说法正确的是( )
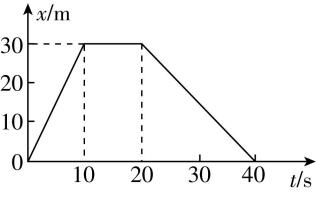 (多选)
(多选)
A.汽车前 $ 5\mathrm{s} $ 内和前 $ 30\mathrm{s} $ 内位移相同
B.汽车前 $ 10\mathrm{s} $ 内的位移为 $ 30\mathrm{m} $ ,后 $ 20\mathrm{s} $ 内位移为 $ 30\mathrm{m} $
C.汽车前 $ 10\mathrm{s} $ 内的平均速度为 $ 3\mathrm{m}/\mathrm{s} $ ,全程平均速度为 $ 1.5\mathrm{m}/\mathrm{s} $
D.汽车前 $ 10\mathrm{s} $ 内的平均速度为 $ 3\mathrm{m}/\mathrm{s} $ ,全程平均速率为 $ 1.5\mathrm{m}/\mathrm{s} $
答案:AD
解析:由题图可知, $ 5\mathrm{s} $ 末、 $ 30\mathrm{s} $ 末汽车的位置均在 $ 15\mathrm{m} $ 处,所以汽车前 $ 5\mathrm{s} $ 内和前 $ 30\mathrm{s} $ 内位移均为 $ 15\mathrm{m} $ ,故 $ \mathrm{A} $ 正确;汽车前 $ 10\mathrm{s} $ 内的位移为 $ 30\mathrm{m} $ ,后 $ 20\mathrm{s} $ 内的位移为 $ -30\mathrm{m} $ ,故 $ \mathrm{B} $ 错误;由题图可知,汽车前 $ 10\mathrm{s} $ 内的平均速度为 $ \overline{v}=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t}=\dfrac{30}{10}\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ ,全程位移为0,所以全程平均速度为0,而全程总路程为 $ 60\mathrm{m} $ ,所以全程平均速率为 $ \overline{v}\prime =\dfrac{s}{t}=\dfrac{60}{40}\mathrm{m}/\mathrm{s}=1.5\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
8.甲、乙两辆汽车在平直公路上同时开始运动,它们的 $ x-t $ 图像如图所示,下列说法正确的是( )
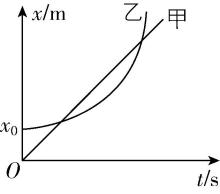 (多选)
(多选)
A. $ t=0 $ 时刻甲汽车的速度小于乙汽车的速度
B. $ t=0 $ 时刻甲汽车的速度大于乙汽车的速度
C.当甲、乙两汽车第二次相遇时,甲汽车的速度小于乙汽车的速度
D.从第一次相遇到第二次相遇,甲汽车的平均速度大于乙汽车的平均速度
答案:BC
解析: $ x-t $ 图像的切线斜率表示物体运动的速度,由题图可知, $ t=0 $ 时刻甲图线的斜率大于乙图线的切线斜率,则甲汽车的速度大于乙汽车的速度,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;甲、乙两汽车第二次相遇时,甲图线的斜率小于乙图线的切线斜率,则甲汽车的速度小于乙汽车的速度,故 $ \mathrm{C} $ 正确;从第一次相遇到第二次相遇,两汽车通过的位移相等,所用时间也相等,则平均速度相同,故 $ \mathrm{D} $ 错误.
9.在一条平直的公路上有甲、乙两辆行驶的汽车,在 $ 0\sim 4\mathrm{s} $ 内两辆汽车的位置坐标 $ x $ 与时间 $ t $ 的关系图像如图所示,则下列说法正确的是( )
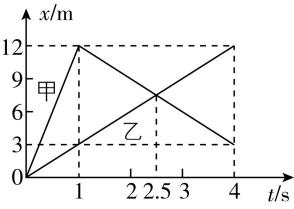 (多选)
(多选)
A.在 $ t=2.5\mathrm{s} $ 时,两辆汽车相遇
B.在 $ t=2.5\mathrm{s} $ 时,两辆汽车速度相同
C.在 $ 0\sim 4\mathrm{s} $ 内,汽车甲的平均速率为 $ 0.75\mathrm{m}/\mathrm{s} $
D.在 $ 0\sim 2.5\mathrm{s} $ 内,两辆汽车的平均速度大小均为 $ 3\mathrm{m}/\mathrm{s} $
答案:AD
解析:由题图可知,两辆汽车在 $ t=2.5\mathrm{s} $ 时出现在同一位置,所以在 $ t=2.5\mathrm{s} $ 时,两辆汽车相遇,故 $ \mathrm{A} $ 正确; $ x-t $ 图像的斜率表示速度,斜率为正表示向正方向运动,斜率为负表示向负方向运动,由题图可知,在 $ t=2.5\mathrm{s} $ 时两辆汽车的速度大小相等,方向相反,故 $ \mathrm{B} $ 错误;在 $ 0\sim 4\mathrm{s} $ 内,汽车甲的路程为 $ {s}_{甲}=12\mathrm{m}+(12-3)\mathrm{m}=21\mathrm{m} $ ,平均速率为 $ v=\dfrac{{s}_{甲}}{t}=5.25\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 错误;在 $ 0\sim 2.5\mathrm{s} $ 内,两辆汽车的位移相同,平均速度相同,由题图可以看出位移 $ \mathrm{\Delta }x=7.5\mathrm{m} $ , $ \overline{v}=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t}=3\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 正确.
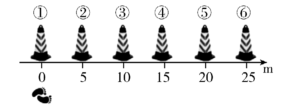
10.直线折返跑是训练足球运动员体能的方式之一.如图将6个标示筒两两间隔 $ 5\mathrm{m} $ 摆放,跑动顺序为 $ \mathrm{①}\to \mathrm{④}\to \mathrm{②}\to \mathrm{⑥} $ ,运动时间为 $ 10\mathrm{s} $ ,则全过程的平均速度大小和平均速率分别为( )
 (多选)
(多选)
A.平均速度大小为 $ 2.5\mathrm{m}/\mathrm{s} $
B.平均速度大小为 $ 3.5\mathrm{m}/\mathrm{s} $
C.平均速率为 $ 6.5\mathrm{m}/\mathrm{s} $
D.平均速率为 $ 4.5\mathrm{m}/\mathrm{s} $
答案:AD
解析:平均速度等于总位移与总时间之比,则有 $ {v}_{1}=\dfrac{5×5}{10}\mathrm{m}/\mathrm{s}=2.5\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;平均速率等于总路程与总时间之比,则有 $ {v}_{2}=\dfrac{5×(3+2+4)}{10}\mathrm{m}/\mathrm{s}=4.5\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
11.一质点始终朝一个方向做直线运动,在前 $ \dfrac{t}{3} $ 时间内平均速度大小为 $ v $ ,在后 $ \dfrac{2t}{3} $ 时间内其平均速度大小为 $ 2v $ ,则此质点在 $ t $ 时间内平均速度的大小为( )
A. $ \dfrac{3v}{5} $
B. $ \dfrac{3v}{2} $
C. $ v $
D. $ \dfrac{5v}{3} $
答案:D
解析:质点在前 $ \dfrac{t}{3} $ 时间内的位移 $ {x}_{1}=v\cdot \dfrac{t}{3} $ ,后 $ \dfrac{2t}{3} $ 时间内的位移 $ {x}_{2}=2v\cdot \dfrac{2t}{3} $ ,根据平均速度的定义式 $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ ,可得质点在 $ t $ 时间内的平均速度大小为 $ \overline{v}=\dfrac{x}{t}=\dfrac{\dfrac{t}{3}\cdot v+\dfrac{2}{3}t\cdot 2v}{t}=\dfrac{5}{3}v $ ,故 $ \mathrm{D} $ 正确.
12.一质点始终向着一个方向做直线运动,在前 $ \dfrac{2}{3}x $ 位移内平均速度为 $ v $ ,后 $ \dfrac{1}{3}x $ 位移内平均速度为 $ 2v $ ,则质点在位移 $ x $ 内的平均速度大小是( )
A. $ \dfrac{4}{3}v $
B. $ \dfrac{6}{5}v $
C. $ \dfrac{4}{5}v $
D. $ \dfrac{3}{2}v $
答案:B
解析:设前 $ \dfrac{2}{3}x $ 位移用时为 $ {t}_{1} $ ,则有 $ {t}_{1}=\dfrac{\dfrac{2}{3}x}{v}=\dfrac{2x}{3v} $ ,设后 $ \dfrac{1}{3}x $ 位移用时为 $ {t}_{2} $ ,则有 $ {t}_{2}=\dfrac{\dfrac{1}{3}x}{2v}=\dfrac{x}{6v} $ ,则质点在位移 $ x $ 内运动的总时间为 $ t={t}_{1}+{t}_{2}=\dfrac{5x}{6v} $ ,则质点在位移 $ x $ 内的平均速度大小为 $ \overline{v}=\dfrac{x}{t}=\dfrac{6}{5}v $ ,故 $ \mathrm{B} $ 正确.
二、刷提升
1.在一次爬山比赛中,某人从山脚爬上山顶,然后又沿原路返回山脚.上山的平均速率为 $ {v}_{1} $ ,下山的平均速率为 $ {v}_{2} $ ,则此人往返一次的平均速度的大小和平均速率是( )
A. $ \dfrac{{v}_{1}+{v}_{2}}{2} $ , $ \dfrac{{v}_{1}+{v}_{2}}{2} $
B. $ \dfrac{{v}_{1}-{v}_{2}}{2} $ , $ \dfrac{{v}_{1}+{v}_{2}}{2} $
C. $ {\rm 0,} \dfrac{{v}_{1}-{v}_{2}}{{v}_{1}+{v}_{2}} $
D. $ {\rm 0,} \dfrac{2{v}_{1}{v}_{2}}{{v}_{1}+{v}_{2}} $
答案:D
解析:设从山脚到山顶的路程为 $ x $ ,此人往返一次对应的位移为0,其平均速度大小为0,而平均速率等于路程与时间的比值,往返一次的平均速率为 $ \overline{v}=\dfrac{x+x}{\dfrac{x}{{v}_{1}}+\dfrac{x}{{v}_{2}}}=\dfrac{2{v}_{1}{v}_{2}}{{v}_{1}+{v}_{2}} $ ,故 $ \mathrm{D} $ 正确.
2.某段高速公路限速 $ 120\mathrm{k}\mathrm{m}/\mathrm{h} $ .监控车辆是否超速的“电子警察”系统如图所示,其工作原理是在路面下相距 $ L $ 的两点埋设两个传感器线圈 $ A $ 和 $ B $ ,当有车辆经过线圈正上方时,传感器能向数据采集器发出一个电信号;若有一辆汽车(可以看作质点)经过该路段,两个传感器先后向数据采集器发送信号,时间间隔为 $ \mathrm{\Delta }t $ ,经微型计算机处理后得出汽车的速度,若超速,则计算机向架设在路面上方的照相机 $ C $ 发出指令,对汽车拍照,留下违章证据.已知 $ L=6\mathrm{m} $ ,则( )

A.若 $ \mathrm{\Delta }t=0.20\mathrm{s} $ ,照相机 $ C $ 会拍照
B.若 $ \mathrm{\Delta }t=0.15\mathrm{s} $ ,照相机 $ C $ 会拍照
C.若 $ \mathrm{\Delta }t=0.20\mathrm{s} $ ,汽车经过线圈 $ A $ 时的瞬时速度大小一定是 $ 30\mathrm{m}/\mathrm{s} $
D.若 $ \mathrm{\Delta }t=0.15\mathrm{s} $ ,汽车经过线圈 $ B $ 时的瞬时速度大小一定是 $ 40\mathrm{m}/\mathrm{s} $
答案:B
解析:计算汽车速度的原理是利用短时间内的平均速度来代替瞬时速度,若汽车刚好全程以最大速度通过 $ AB $ 段,则所需的时间为 $ t=\dfrac{L}{{v}_{\mathrm{m}}}=\dfrac{6}{120}×3.6\mathrm{s}=0.18\mathrm{s} $ ,故当 $ \mathrm{\Delta }t⩾ 0.18\mathrm{s} $ 时,汽车不超速,照相机 $ C $ 不会拍照,当 $ \mathrm{\Delta }t < 0.18\mathrm{s} $ 时,汽车超速,照相机 $ C $ 会拍照,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;若 $ \mathrm{\Delta }t=0.20\mathrm{s} $ ,则汽车通过 $ AB $ 段的平均速度为 $ \overline{v}=\dfrac{6}{0.20}\mathrm{m}/\mathrm{s}=30\mathrm{m}/\mathrm{s} $ ,即汽车的平均速度大小为 $ 30\mathrm{m}/\mathrm{s} $ ,但汽车通过线圈 $ A $ 时的瞬时速度大小不一定是 $ 30\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 错误;若 $ \mathrm{\Delta }t=0.15\mathrm{s} $ ,则汽车通过 $ AB $ 段的平均速度为 $ \overline{v}\prime =\dfrac{6}{0.15}\mathrm{m}/\mathrm{s}=40\mathrm{m}/\mathrm{s} $ ,即汽车的平均速度大小为 $ 40\mathrm{m}/\mathrm{s} $ ,但汽车通过线圈 $ B $ 时的瞬时速度大小不一定是 $ 40\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 错误.
3.在平直公路上行驶的 $ a $ 车和 $ b $ 车,其位置 $ (x)— $ 时间 $ (t) $ 图像分别为图中直线 $ a $ 和曲线 $ b $ ,由图可知( )
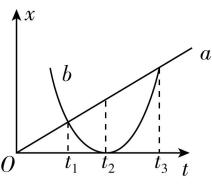
A. $ {t}_{1} $ 到 $ {t}_{3} $ 时间内, $ a $ 车与 $ b $ 车的平均速度相同
B.在 $ {t}_{3} $ 时刻 $ a $ 车与 $ b $ 车速度相同
C. $ {t}_{1}\sim {t}_{2} $ 时间内, $ b $ 车沿正方向做减速运动
D. $ a $ 车与 $ b $ 车运动过程中运动方向始终不变
答案:A
解析:以 $ a $ 车运动的初始位置为原点 $ O $ ,将题给位置—时间图像转化成位移—时间图像,根据位移—时间图像在某段时间内的位移等于纵坐标的变化量,由题图可知 $ {t}_{1} $ 到 $ {t}_{3} $ 时间内 $ a $ 车的位移等于 $ b $ 车的位移,根据平均速度公式 $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ ,可知 $ {t}_{1} $ 到 $ {t}_{3} $ 时间内 $ a $ 车与 $ b $ 车的平均速度相同,故 $ \mathrm{A} $ 正确;根据位移—时间图像切线斜率代表速度,可知在 $ {t}_{3} $ 时刻 $ a $ 车与 $ b $ 车速度不同,故 $ \mathrm{B} $ 错误;由题图可知, $ {t}_{1}\sim {t}_{2} $ 时间内, $ b $ 车沿负方向做减速运动,故 $ \mathrm{C} $ 错误; $ b $ 车的位移—时间图像的切线斜率的正负在 $ {t}_{2} $ 时刻发生变化,则运动方向发生变化,故 $ \mathrm{D} $ 错误.
4.央视军事宣传片《淬火》曝光了一起震撼的海上对峙事件:长沙舰在南海西沙海域与外舰对峙47小时,以一敌三,展现了我国海军强大的战斗意志和冷静的态度.如图所示为长沙舰某次海域巡航活动路线图,长沙舰从 $ A $ 港出发先沿正东方向以 $ 30\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度运动 $ 3\mathrm{h} $ 到达 $ B $ 处,然后沿正北方向以 $ 40\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度运动 $ 3\mathrm{h} $ 到达小岛 $ C $ 处.求:
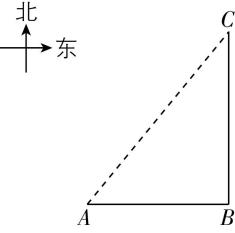
(1) 该过程中长沙舰的路程和位移大小;
(2) 该过程中长沙舰的平均速率和平均速度大小.
答案:(1) $ 210\mathrm{k}\mathrm{m} $ ; $ 150\mathrm{k}\mathrm{m} $
(2) $ 35\mathrm{k}\mathrm{m}/\mathrm{h} $ ; $ 25\mathrm{k}\mathrm{m}/\mathrm{h} $
解析:(1) 长沙舰向东运动的位移大小为 $ x={v}_{1}{t}_{1}=30×3\mathrm{k}\mathrm{m}=90\mathrm{k}\mathrm{m} $ ,再向北运动的位移大小为 $ y={v}_{2}{t}_{2}=40×3\mathrm{k}\mathrm{m}=120\mathrm{k}\mathrm{m} $ ,则该过程中长沙舰的位移大小为 $ l=\sqrt{{x}^{2}+{y}^{2}} $ ,解得 $ l=150\mathrm{k}\mathrm{m} $ ,长沙舰的路程为 $ s=x+y=90\mathrm{k}\mathrm{m}+120\mathrm{k}\mathrm{m}=210\mathrm{k}\mathrm{m} $ .
(2) 该过程中长沙舰的平均速率 $ v=\dfrac{s}{t}=\dfrac{210}{6}\mathrm{k}\mathrm{m}/\mathrm{h}=35\mathrm{k}\mathrm{m}/\mathrm{h} $ ,长沙舰的平均速度大小 $ \overline{v}=\dfrac{l}{t}=\dfrac{150}{6}\mathrm{k}\mathrm{m}/\mathrm{h}=25\mathrm{k}\mathrm{m}/\mathrm{h} $ .
5.小船以速度 $ v $ 从河边 $ A $ 处沿河岸划行至 $ B $ 处又返回 $ A $ 处.不计船掉头时间,若河水不流动时往返一次时间为 $ t $ ,那么河水流速为 $ {v}_{0} $ 时,往返 $ A $ 、 $ B $ 一次的时间为( )
A. $ \dfrac{{v}^{2}}{{v}^{2}-{v}_{0}^{2}}t $
B. $ \dfrac{{v}^{2}}{{v}^{2}+{v}_{0}^{2}}t $
C. $ \dfrac{v}{v-{v}_{0}}t $
D. $ \dfrac{v}{v+{v}_{0}}t $
答案:A
解析:水不流动时,小船通过的路程为 $ A $ 点到 $ B $ 点距离的两倍,设 $ A $ 、 $ B $ 点间距离为 $ s $ ,则有 $ 2s=vt $ ,故 $ A $ 点到 $ B $ 点之间的距离 $ s=\dfrac{vt}{2} $ ;若河水流速为 $ {v}_{0} $ ,则顺水速度为 $ v+{v}_{0} $ ,顺水运动所用的时间为 $ {t}_{AB}=\dfrac{s}{v+{v}_{0}} $ ;逆水速度为 $ v-{v}_{0} $ ,逆水运动所用的时间为 $ {t}_{BA}=\dfrac{s}{v-{v}_{0}} $ ,则往返时间为 $ t\prime =\dfrac{s}{v+{v}_{0}}+\dfrac{s}{v-{v}_{0}}=\dfrac{{v}^{2}}{{v}^{2}-{v}_{0}^{2}}t $ ,故 $ \mathrm{A} $ 正确.



 (多选)
(多选) (多选)
(多选) (多选)
(多选) (多选)
(多选)

