1.为了研究位移与时间的关系,物理兴趣实验小组将位移传感器佩戴在 $ A $ 和 $ B $ 两位同学的身上,让他们在操场上沿直线运动,记录了他们运动的位置—时间图像如图所示,下列说法中正确的是( )
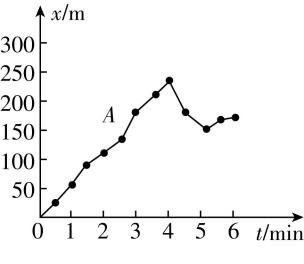
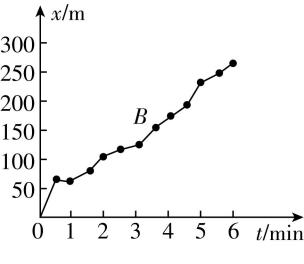
A.在 $ 0\sim 6 \min $ 内, $ B $ 同学的平均速度较大
B.在 $ t=1 \min $ 时刻, $ A $ 同学的速度较大
C.在 $ 0\sim 6 \min $ 内, $ B $ 同学始终在加速
D.在 $ 0\sim 6 \min $ 内, $ A $ 同学始终沿着一个方向运动
答案:AB
解析:根据 $ x-t $ 图像中纵坐标的变化量表示位移,可知 $ 0\sim 6 \min $ 内, $ B $ 同学的位移大于 $ A $ 同学的位移,则 $ B $ 同学的平均速度较大,故 $ \mathrm{A} $ 正确;根据 $ x-t $ 图像中图线的斜率表示速度,可知在 $ t=1 \min $ 时刻, $ A $ 同学的 $ x-t $ 图线斜率较大,则 $ A $ 同学的速度较大,故 $ \mathrm{B} $ 正确;根据 $ x-t $ 图像中图线的斜率表示速度,可知在 $ 0\sim 6 \min $ 内, $ B $ 同学的速度不是一直增大,故 $ \mathrm{C} $ 错误;根据 $ x-t $ 图线斜率的正负表示速度的方向,可知 $ A $ 同学在 $ t=4 \min $ 时刻和 $ t=5 \min $ 时刻运动方向发生改变,故 $ \mathrm{D} $ 错误.
2.如图甲所示是一种速度传感器的工作原理图,在这个系统中 $ B $ 为一个能发射超声波的固定装置,工作时 $ B $ 向匀速直线运动的被测物体发出短暂的超声波脉冲,超声波速度为 $ {v}_{0} $ ,脉冲被运动的物体反射后又被 $ B $ 接收到,从 $ B $ 发射超声波开始计时,经 $ \mathrm{\Delta }{t}_{0} $ 时间再次发射超声波脉冲,图乙是连续两次发射的超声波的位置—时间图像.则下列说法正确的是( )
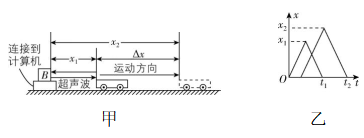
A.脉冲第一次被运动的物体反射时,物体与 $ B $ 间的距离 $ {x}_{1}={v}_{0}{t}_{1} $
B.脉冲第二次被运动的物体反射时,物体与 $ B $ 间的距离 $ {x}_{2}=\dfrac{{v}_{0}{t}_{2}}{2} $
C.物体的平均速度大小为 $ \overline{v}=\dfrac{2({x}_{2}-{x}_{1})}{{t}_{2}-{t}_{1}+2\mathrm{\Delta }{t}_{0}} $
D.物体的平均速度大小为 $ \overline{v}=\dfrac{2({x}_{2}-{x}_{1})}{{t}_{2}-{t}_{1}+\mathrm{\Delta }{t}_{0}} $
答案:D
解析:由题图乙可知,脉冲第一次被运动的物体反射时,物体与 $ B $ 间的距离 $ {x}_{1}={v}_{0}\cdot \dfrac{{t}_{1}}{2} $ ,故 $ \mathrm{A} $ 错误;脉冲第二次被运动的物体反射时,物体与 $ B $ 间的距离 $ {x}_{2}={v}_{0}\cdot \dfrac{{t}_{2}-\mathrm{\Delta }{t}_{0}}{2} $ ,故 $ \mathrm{B} $ 错误;由题可知,物体运动 $ \mathrm{\Delta }x={x}_{2}-{x}_{1} $ 的距离所用时间为 $ t=\dfrac{{t}_{2}-\mathrm{\Delta }{t}_{0}}{2}+\mathrm{\Delta }{t}_{0}-\dfrac{{t}_{1}}{2}=\dfrac{1}{2}({t}_{2}-{t}_{1}+\mathrm{\Delta }{t}_{0}) $ ,物体的平均速度大小为 $ \overline{v}=\dfrac{\mathrm{\Delta }x}{t}=\dfrac{2({x}_{2}-{x}_{1})}{{t}_{2}-{t}_{1}+\mathrm{\Delta }{t}_{0}} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
3.某兴趣小组的同学在做“用打点计时器测速度”的实验中,让重锤自由下落,打出的一条纸带如图所示,图中直尺的单位为 $ \mathrm{c}\mathrm{m} $ ,点 $ O $ 为纸带上记录到的第一个点,点 $ A $ 、 $ B $ 、 $ C $ 、 $ D\cdots $ 依次表示点 $ O $ 以后连续打出的各点,已知打点计时器每隔 $ T=0.02\mathrm{s} $ 打一个点.

(1) 纸带的 (填“左端”或“右端”)与重锤相连.
(2) $ {x}_{OF}= $ $ \mathrm{c}\mathrm{m} $ , $ {x}_{OH}= $ $ \mathrm{c}\mathrm{m} $ , $ FH $ 段的平均速度大小为 $ \overline{v}= $ $ \mathrm{m}/\mathrm{s} $ .
(3) 如果当时交变电流的频率是 $ f=51\mathrm{H}\mathrm{z} $ ,而计算时仍按 $ f=50\mathrm{H}\mathrm{z} $ 处理,那么速度的测量值将 (填“偏大”“偏小”或“不变”). $ ( $ 已知 $ T=\dfrac{1}{f}) $
答案:(1) 左端
(2) 6.10;11.40;1.325
(3) 偏小
解析:(1) 纸带下落过程中,速度越来越大,相等时间间隔的位移越来越大,则点迹间距不断增大,由题图知,从左到右点迹间距逐渐增大,则纸带的左端与重锤相连.
(2) 由题图可知, $ {x}_{OF}=6.10\mathrm{c}\mathrm{m} $ , $ {x}_{OH}=11.40\mathrm{c}\mathrm{m} $ , $ {x}_{FH}={x}_{OH}-{x}_{OF}=11.40\mathrm{c}\mathrm{m}-6.10\mathrm{c}\mathrm{m}=5.30×{10}^{-2}\mathrm{m} $ ,则 $ \overline{v}=\dfrac{5.30×{10}^{-2}}{2×0.02}\mathrm{m}/\mathrm{s}=1.325\mathrm{m}/\mathrm{s} $ .
(3) 如果 $ f=51\mathrm{H}\mathrm{z} > 50\mathrm{H}\mathrm{z} $ ,根据 $ T=\dfrac{1}{f} $ ,则实际打点周期偏小,计时所用数据偏大,由 $ v=\dfrac{x}{t} $ 可知,速度测量值将小于真实值.
4.如图所示,一条水平长直轨道上有两辆小车,甲车向左运动,速度大小为 $ {v}_{1} $ ,乙车向右运动,速度大小为 $ {v}_{2} $ ,甲车上装有一只玩具枪,每隔 $ \mathrm{\Delta }{t}_{0} $ 时间水平射出一颗子弹,都能击中装在乙车上的靶子,不计子弹的重力和空气阻力,每颗子弹对地速度保持 $ {v}_{0} $ 不变,每颗子弹击中靶时下一颗子弹已经射出,设两车速度不受子弹射击影响,求:
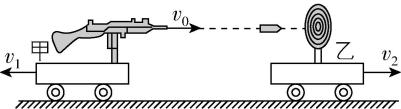
(1) 空中相邻两颗子弹间的距离 $ s $ ;
(2) 相邻两颗子弹击中靶的间隔时间 $ \mathrm{\Delta }t $ 的大小.
答案:(1) $ ({v}_{0}+{v}_{1})\cdot \mathrm{\Delta }{t}_{0} $
(2) $ \dfrac{({v}_{0}+{v}_{1})\mathrm{\Delta }{t}_{0}}{{v}_{0}-{v}_{2}} $
解析:(1) 对于射出的子弹,在时间 $ \mathrm{\Delta }{t}_{0} $ 内运动的距离为 $ {s}_{1}={v}_{0}\cdot \mathrm{\Delta }{t}_{0} $ ,小车甲在时间 $ \mathrm{\Delta }{t}_{0} $ 内运动的距离为 $ {s}_{2}={v}_{1}\cdot \mathrm{\Delta }{t}_{0} $ ,所以空中相邻两颗子弹间的距离为 $ s={s}_{1}+{s}_{2}=({v}_{0}+{v}_{1})\cdot \mathrm{\Delta }{t}_{0} $ .
(2) 当一颗子弹击中靶后,下一颗子弹运动的距离为 $ {s}_{3}={v}_{0}\cdot \mathrm{\Delta }t $ ,这一段时间内小车乙运动的距离为 $ {s}_{4}={v}_{2}\cdot \mathrm{\Delta }t $ ,下一颗子弹击中靶时,有 $ s={s}_{3}-{s}_{4}=({v}_{0}-{v}_{2})\cdot \mathrm{\Delta }t $ ,联立解得 $ \mathrm{\Delta }t=\dfrac{({v}_{0}+{v}_{1})\mathrm{\Delta }{t}_{0}}{{v}_{0}-{v}_{2}} $ .




