第4节 速度变化快慢的描述——加速度
一、刷基础
1.以下关于加速度的说法中正确的是( )
A.加速度越大,则在相同的时间内速度改变量就越大
B.加速度增大,则物体的速度也增大
C.加速度越大,则物体的速度也越大
D.速率不变,则物体的加速度为零
答案:A
解析:根据加速度定义式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ ,可知加速度越大,则在相同的时间内速度改变量就越大,故 $ \mathrm{A} $ 正确;若加速度方向与速度方向相反,物体做减速运动,加速度增大,物体的速度减小,故 $ \mathrm{B} $ 错误;加速度与速度无必然联系,加速度越大,物体的速度不一定越大,故 $ \mathrm{C} $ 错误;速率不变时,速度的方向可能改变,此时加速度不为零,故 $ \mathrm{D} $ 错误.
2.甲、乙两物体的速度分别为 $ {v}_{甲}=1\mathrm{m}/\mathrm{s} $ 、 $ {v}_{乙}=-5\mathrm{m}/\mathrm{s} $ ,丙、丁两物体的加速度分别为 $ {a}_{丙}=1\mathrm{m}/{\mathrm{s}}^{2} $ 、 $ {a}_{丁}=-5\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法正确的是( )
A.甲物体的速度大于乙物体的速度
B.丙物体的加速度大于丁物体的加速度
C.若乙物体做匀速直线运动,则 $ 1\mathrm{s} $ 内乙物体的位移大小为 $ 5\mathrm{m} $
D.丁物体不可能做匀加速直线运动
答案:C
解析:矢量的正负表示方向,不表示大小,矢量的大小只取决于数值的大小,速度和加速度都是矢量,所以甲的速度小于乙的速度,丙的加速度小于丁的加速度, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;若乙做匀速直线运动,根据匀速直线运动公式得 $ 1\mathrm{s} $ 内乙的位移大小 $ x=|{v}_{乙}|\cdot t=5\mathrm{m} $ , $ \mathrm{C} $ 正确;若丁物体的速度方向和加速度方向相同,则其做匀加速直线运动, $ \mathrm{D} $ 错误.
3.关于表格中的数据,下列说法正确的是( )
运动 | $ a/(\mathrm{m}\cdot {\mathrm{s}}^{-2}) $ | 运动 | $ a/(\mathrm{m}\cdot {\mathrm{s}}^{-2}) $ |
子弹在枪筒中 | $ 5×{10}^{4} $ | 赛车起步 | 4.5 |
跳伞者着陆 | $ -25 $ | 汽车起步 | 2 |
汽车急刹车 | $ -5 $ | 高铁起步 | 0.35 |
A.子弹的加速度最大,子弹的速度变化最快
B.跳伞者的加速度最小,跳伞者的速度变化最慢
C.高铁的加速度最小,其速度变化量一定最小
D.汽车在刹车过程中,位移是逐渐变小的
答案:A
解析:由表格数据可知,子弹的加速度最大,则子弹的速度变化最快;高铁起步的加速度最小,则高铁的速度变化最慢,但其速度变化量不一定最小,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误.汽车在刹车过程中的速度方向保持不变,所以汽车的位移是逐渐增大的,故 $ \mathrm{D} $ 错误.
4.在某次台球比赛中,某运动员将台球甲从距离台球乙 $ {x}_{1}=1.5\mathrm{m} $ 处对准静止的台球乙击出,台球甲经过 $ {t}_{1}=0.25\mathrm{s} $ 后以 $ {v}_{1}=5\mathrm{m}/\mathrm{s} $ 的速度击中台球乙,两者碰撞后台球甲以 $ {v}_{2}=1\mathrm{m}/\mathrm{s} $ 的速度、台球乙以 $ {v}_{3}=4\mathrm{m}/\mathrm{s} $ 的速度均沿台球甲碰撞前运动方向运动,台球甲、乙碰撞的时间 $ \mathrm{\Delta }t=0.005\mathrm{s} $ .求:
(1) 台球甲从被击出到击中台球乙前的平均速度大小 $ \overline{v} $ ;
(2) 台球甲在碰撞过程中的平均加速度大小 $ {a}_{1} $ ;
(3) 台球乙在碰撞过程中的平均加速度大小 $ {a}_{2} $ .
答案:(1) $ 6\mathrm{m}/\mathrm{s} $
(2) $ 800\mathrm{m}/{\mathrm{s}}^{2} $
(3) $ 800\mathrm{m}/{\mathrm{s}}^{2} $
解析:(1) 台球甲从被击出到击中台球乙前的平均速度大小 $ \overline{v}=\dfrac{{x}_{1}}{{t}_{1}}=6\mathrm{m}/\mathrm{s} $ .
(2) 根据加速度的定义式可得,台球甲在碰撞过程中的平均加速度大小 $ {a}_{1}=|\dfrac{{v}_{2}-{v}_{1}}{\mathrm{\Delta }t}|=800\mathrm{m}/{\mathrm{s}}^{2} $ .
(3) 根据加速度的定义式可得,台球乙在碰撞过程中的平均加速度大小 $ {a}_{2}=|\dfrac{{v}_{3}}{\mathrm{\Delta }t}|=800\mathrm{m}/{\mathrm{s}}^{2} $ .
5.如图所示为研究汽车速度变化时的示意图,若汽车原来的速度是 $ {v}_{1} $ ,经过一小段时间 $ \mathrm{\Delta }t $ 之后速度变为 $ {v}_{2} $ ,在图中以原来的速度 $ {v}_{1} $ 的箭头端为起点,以后来的速度 $ {v}_{2} $ 的箭头端为终点,作出一个新的带箭头的有向线段,用它表示速度的变化量 $ \mathrm{\Delta }v $ .则以下说法中正确的是( )
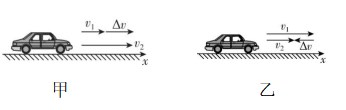
A.图甲中汽车正在做加速运动,图乙中汽车正在做减速运动
B.速度的变化量 $ \mathrm{\Delta }v $ 越大,加速度也越大
C.速度较小的汽车,其加速度也较小,速度较大的汽车,其加速度也较大
D.汽车加速时,其加速度方向与 $ \mathrm{\Delta }v $ 方向相同,汽车减速时,其加速度方向与 $ \mathrm{\Delta }v $ 方向相反
答案:A
解析:题图甲中 $ {v}_{2} > {v}_{1} $ ,即汽车速度在增大,所以题图甲中汽车正在做加速运动;题图乙中 $ {v}_{2} < {v}_{1} $ ,即汽车速度在减小,所以题图乙中汽车正在做减速运动, $ \mathrm{A} $ 正确.由加速度的定义式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 可知,在相同的时间内,速度的变化量 $ \mathrm{\Delta }v $ 越大,加速度越大, $ \mathrm{B} $ 错误.加速度反映的是物体速度变化的快慢,与物体速度的大小无直接关系, $ \mathrm{C} $ 错误.由加速度的定义式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 可知,加速度的方向与速度的变化量 $ \mathrm{\Delta }v $ 的方向相同,与汽车做加速运动还是减速运动无关, $ \mathrm{D} $ 错误.
6.如图为蜻蜓、火箭的运动示意图.图甲中以 $ 8\mathrm{m}/\mathrm{s} $ 的速度飞行的蜻蜓能在 $ 0.7\mathrm{s} $ 内停下来;图乙中火箭发射后 $ 10\mathrm{s} $ 内速度由0增加到 $ 100\mathrm{m}/\mathrm{s} $ .

(1) 计算蜻蜓和火箭加速度的大小并说明谁的速度变化快;
(2) 分析蜻蜓和火箭的加速度方向与速度方向的关系;
(3) 试根据上述情景和问题分析:在直线运动中物体做加速运动或减速运动的条件.
答案:(1) $ 11.4\mathrm{m}/{\mathrm{s}}^{2} $ ; $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ;蜻蜓的速度变化快
(2) 蜻蜓的加速度方向与速度方向相反;火箭的加速度方向与速度方向相同
(3) 见解析
解析:(1) 蜻蜓的加速度为 $ {a}_{1}=\dfrac{\mathrm{\Delta }{v}_{1}}{\mathrm{\Delta }{t}_{1}}=\dfrac{0-8}{0.7}\mathrm{m}/{\mathrm{s}}^{2}=-11.4\mathrm{m}/{\mathrm{s}}^{2} $ ,火箭的加速度为 $ {a}_{2}=\dfrac{\mathrm{\Delta }{v}_{2}}{\mathrm{\Delta }{t}_{2}}=\dfrac{100-0}{10}\mathrm{m}/{\mathrm{s}}^{2}=10\mathrm{m}/{\mathrm{s}}^{2} $ ,蜻蜓和火箭加速度的大小分别为 $ 11.4\mathrm{m}/{\mathrm{s}}^{2} $ 和 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,且 $ 11.4\mathrm{m}/{\mathrm{s}}^{2} > 10\mathrm{m}/{\mathrm{s}}^{2} $ ,则蜻蜓速度变化快.
(2) 根据第(1)问,可知蜻蜓的加速度为负值,表示其方向与速度方向相反;火箭的加速度为正值,表示其方向与速度方向相同.
(3) 根据第(1)问,可得在直线运动中,当加速度方向与速度方向相同时,物体做加速运动;当加速度方向与速度方向相反时,物体做减速运动.
7.一枚火箭由地面竖直向上发射,其速度—时间图像如图所示,由图像可知( )
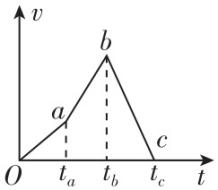
A. $ {t}_{c} $ 时刻火箭回到地面
B. $ 0\sim {t}_{a} $ 段火箭处在上升过程, $ {t}_{a}\sim {t}_{b} $ 段火箭处在下落过程
C. $ {t}_{b} $ 时刻火箭离地面最远
D. $ 0\sim {t}_{a} $ 段火箭的加速度小于 $ {t}_{a}\sim {t}_{b} $ 段的火箭加速度
答案:D
解析:根据 $ v-t $ 图像的斜率表示加速度,可知 $ 0\sim {t}_{a} $ 段火箭的加速度小于 $ {t}_{a}\sim {t}_{b} $ 段火箭的加速度,故 $ \mathrm{D} $ 正确;根据 $ v-t $ 图像可知, $ 0\sim {t}_{c} $ 内 $ v $ 始终大于0,可知 $ 0\sim {t}_{c} $ 段火箭都处在上升过程,则 $ {t}_{c} $ 时刻火箭离地面最远,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误.
8.一物体做直线运动,其加速度随时间变化的 $ a-t $ 图像如图所示.下列 $ v-t $ 图像中,能正确描述此物体运动的是( )
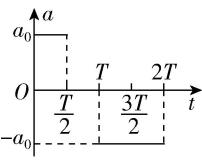
A.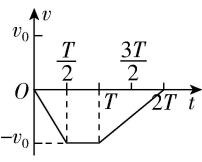
B.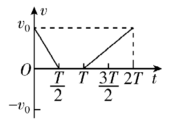
C.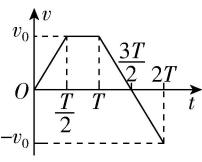
D.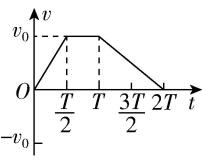
答案:C
解析: $ t=0 $ 时刻,若物体的初速度为零,根据 $ a-t $ 图像可知, $ 0\sim \dfrac{T}{2} $ 内物体向正方向做加速度大小不变的加速直线运动; $ \dfrac{T}{2}\sim T $ 内物体向正方向做匀速直线运动; $ T\sim \dfrac{3T}{2} $ 内物体向正方向做加速度大小不变的减速直线运动, $ \dfrac{3}{2}T $ 时刻物体的速度为0; $ \dfrac{3T}{2}\sim 2T $ 内物体向负方向做加速度大小不变的加速直线运动,且 $ 0\sim \dfrac{T}{2} $ 内和 $ T\sim 2T $ 内物体的加速度大小相同,方向相反,故 $ \mathrm{C} $ 正确.
9.升降机直线提升重物,重物运动的 $ v-t $ 图像如图所示,取竖直向上为正方向,求:
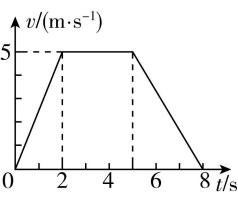
(1) 重物在 $ 0\sim 2\mathrm{s} $ 、 $ 2\sim 5\mathrm{s} $ 和 $ 5\sim 8\mathrm{s} $ 的时间内分别做什么运动?
(2) $ 0\sim 2\mathrm{s} $ 与 $ 5\sim 8\mathrm{s} $ 内重物的加速度大小和方向.
答案:(1) 加速直线运动;匀速直线运动;减速直线运动
(2) $ 2.5\mathrm{m}/{\mathrm{s}}^{2} $ ,方向竖直向上; $ \dfrac{5}{3}\mathrm{m}/{\mathrm{s}}^{2} $ ,方向竖直向下
解析:(1) 由 $ v-t $ 图像可知 $ 0\sim 2\mathrm{s} $ 内图线是一条倾斜的直线且速度为正、加速度为正,两者方向相同,则重物做加速直线运动, $ 2\sim 5\mathrm{s} $ 内图线是一条平行于 $ t $ 轴的直线,则重物做匀速直线运动, $ 5\sim 8\mathrm{s} $ 内图线是一条倾斜的直线且速度为正、加速度为负,则重物做减速直线运动.
(2) 由加速度的定义式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 结合 $ v-t $ 图像,在 $ 0\sim 2\mathrm{s} $ 内、 $ 5\sim 8\mathrm{s} $ 内分别代入数据,有 $ {a}_{1}=2.5\mathrm{m}/{\mathrm{s}}^{2} $ ,方向竖直向上, $ {a}_{2}=\dfrac{5}{3}\mathrm{m}/{\mathrm{s}}^{2} $ ,方向竖直向下.
10.如图所示,在足够长的固定光滑斜面上,一小物块以大小为 $ 8\mathrm{m}/\mathrm{s} $ 的初速度从 $ A $ 点沿斜面向上做加速度不变的直线运动, $ 2\mathrm{s} $ 后到达 $ B $ 点(图中未画出),小物块到达 $ B $ 点时的速度大小为 $ 2\mathrm{m}/\mathrm{s} $ .小物块在斜面上运动的加速度大小可能为( )
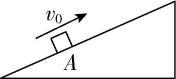 (多选)
(多选)
A. $ 2\mathrm{m}/{\mathrm{s}}^{2} $
B. $ 3\mathrm{m}/{\mathrm{s}}^{2} $
C. $ 4\mathrm{m}/{\mathrm{s}}^{2} $
D. $ 5\mathrm{m}/{\mathrm{s}}^{2} $
答案:BD
解析:以初速度的方向为正方向,则初速度 $ {v}_{0}=8\mathrm{m}/\mathrm{s} $ ,当末速度为 $ {v}_{1}=2\mathrm{m}/\mathrm{s} $ 时,由加速度定义式得 $ {a}_{1}=\dfrac{{v}_{1}-{v}_{0}}{t}=-3\mathrm{m}/{\mathrm{s}}^{2} $ ,负号表示方向与初速度方向相反;当末速度为 $ {v}_{2}=-2\mathrm{m}/\mathrm{s} $ 时,由加速度定义式得 $ {a}_{2}=\dfrac{{v}_{2}-{v}_{0}}{t}=-5\mathrm{m}/{\mathrm{s}}^{2} $ ,负号表示方向与初速度方向相反,故 $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确.
11.一骑行爱好者在平直公路上骑行,从某时刻开始刹车下坡,自行车的加速度沿斜坡向上,其值由零逐渐增大到某一值后又立即逐渐减小到零(自行车始终在运动),在该过程中自行车( )(多选)
A.速度一直减小,直到加速度减小到零为止
B.速度先增大后减小,直到加速度减小到零为止
C.位移先增大后减小,直到加速度减小到零为止
D.位移一直增大,加速度减小到零之后位移仍继续增大
答案:AD
解析:自行车的运动方向沿斜坡向下,加速度方向沿斜坡向上,所以速度一直减小,位移一直在增大,当加速度减小到零后做匀速直线运动,故 $ \mathrm{A} $ 、 $ \mathrm{D} $ 正确.
二、刷提升
1.一质点自原点开始在 $ x $ 轴上运动,初速度 $ {v}_{0} > 0 $ ,加速度 $ a > 0 $ , $ a $ 值不断减小直至为零的过程中,质点的( )(多选)
A.速度不断减小,位移一定减小
B.速度不断增大,位移一定增大
C.速度不断增大,当 $ a=0 $ 时,速度达到最大
D.速度不断减小,当 $ a=0 $ 时,速度达到最小
答案:BC
解析:由于初速度 $ {v}_{0} > 0 $ ,加速度 $ a > 0 $ ,即速度和加速度同向,不管加速度大小如何变化,速度都是在增加的,当加速度减小时,相同时间内速度的增加量变小,即增加得慢了;当 $ a=0 $ 时,速度达到最大值,此后以该最大速度做匀速直线运动,位移不断增大, $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确.
2.汽车的“ $ G $ 值”是一个用来量化某一加速区间汽车加速性能的参数,测试中,“ $ G $ 值”是在一定加速区间测得的加速度的平均值除以重力加速度 $ g $ 得到的数.某型号汽车在 $ 0\sim 100\mathrm{k}\mathrm{m}/\mathrm{h} $ 加速性能测试中,测得的加速时间是 $ 6.2\mathrm{s} $ ,重力加速度 $ g $ 取 $ 9.8\mathrm{m}/{\mathrm{s}}^{2} $ ,由此推算,该车的“ $ G $ 值”约为( )
A.1.6
B.1.0
C.0.46
D.0.30
答案:C
解析:由题意有 $ v=100\mathrm{k}\mathrm{m}/\mathrm{h}=\dfrac{100}{3.6}\mathrm{m}/\mathrm{s} $ , $ {v}_{0}=0 $ ,根据加速度的定义式得该汽车的平均加速度为 $ a=\dfrac{v-{v}_{0}}{t}=4.48\mathrm{m}/{\mathrm{s}}^{2} $ ,由题意知该车的“ $ G $ 值”约为 $ \dfrac{a}{g}=0.46 $ ,故选 $ \mathrm{C} $ .
3.我国海军在亚丁湾索马里海域护航时,有六艘海盗快艇试图靠近中国海军护航编队保护的商船,中国特战队员发射爆震弹成功将其驱离.假如其中一艘海盗快艇在海面上运动的 $ v-t $ 图像如图所示,下列说法正确的是( )
 (多选)
(多选)
A.海盗快艇在 $ 0\sim 66\mathrm{s} $ 内从静止出发做加速度增大的加速直线运动
B.海盗快艇在 $ 96\mathrm{s} $ 末开始掉头逃离
C.海盗快艇在 $ 66\mathrm{s} $ 末开始掉头逃离
D.海盗快艇在 $ 96\sim 116\mathrm{s} $ 内的加速度为 $ a=-0.75\mathrm{m}/{\mathrm{s}}^{2} $
答案:BD
解析:速度—时间图像的切线斜率表示加速度,在 $ 0\sim 66\mathrm{s} $ 内题图图线的切线斜率越来越小,加速度越来越小,故海盗快艇做加速度减小的加速直线运动,故 $ \mathrm{A} $ 错误;海盗快艇在 $ 96\mathrm{s} $ 末速度由正值变为负值,速度方向发生变化,即改变运动的方向,开始掉头逃离,故 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;在 $ 96\sim 116\mathrm{s} $ 内,根据加速度定义式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 可得 $ a=\dfrac{-15-0}{116-96}\mathrm{m}/{\mathrm{s}}^{2}=-0.75\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{D} $ 正确.
4.一辆摩托车沿直线运动时,速度随时间变化的数据见下表.摩托车在 $ 0\mathrm{~}15\mathrm{s} $ 和 $ 15\mathrm{~}30\mathrm{s} $ 两段时间内视为做加速度不变的直线运动.
$ t/\mathrm{s} $ | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
$ v/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $ | 0 | 10 | 20 | 30 | 20 | 10 | 0 |
(1) 求摩托车在第一个 $ 10\mathrm{s} $ 内的加速度;
(2) 根据表中数据作出摩托车运动的 $ v-t $ 图像;
(3) 根据画出的 $ v-t $ 图像求出第一个 $ 10\mathrm{s} $ 内的加速度,并与(1)中的计算结果进行比较;
(4) 求摩托车在 $ 15\mathrm{~}30\mathrm{s} $ 内的加速度.
答案:(1) $ 2\mathrm{m}/{\mathrm{s}}^{2} $ ,方向与运动方向相同
(2) 见解析
(3) $ 2\mathrm{m}/{\mathrm{s}}^{2} $ ,方向与运动方向相同与(1)中的计算结果相同
(4) $ 2\mathrm{m}/{\mathrm{s}}^{2} $ ,方向与运动方向相反
解析:(1) 根据加速度的定义式可得 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\dfrac{20}{10}\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,方向与运动方向相同.
(2) 摩托车运动的 $ v-t $ 图像如图所示.
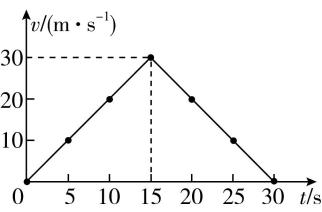
(3) $ v-t $ 图像的斜率表示加速度,摩托车第一个 $ 10\mathrm{s} $ 内的加速度 $ a\prime =k=\dfrac{30}{15}\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,方向与运动方向相同,与(1)中的计算结果相同.
(4) 摩托车在 $ 15\mathrm{~}30\mathrm{s} $ 内的加速度为 $ {a}_{1}=\dfrac{\mathrm{\Delta }v\prime }{\mathrm{\Delta }t\prime }=\dfrac{0-30}{15}\mathrm{m}/{\mathrm{s}}^{2}=-2\mathrm{m}/{\mathrm{s}}^{2} $ ,负号表示加速度方向与运动方向相反.
5.近年来,一些高级轿车的设计师提出了“加速度的变化率”的概念,用这一新的概念来描述轿车加速度随时间变化的快慢,轿车的“加速度的变化率”越小,乘坐轿车的人感觉越舒适.图示是一辆汽车在水平公路上行驶时加速度随时间变化的关系图像(在 $ a-t $ 图像中图像与时间轴所围图形的面积表示物体速度的变化量),则下列说法正确的是( )
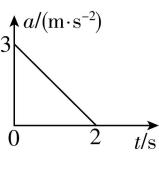 (多选)
(多选)
A.从运动学角度定义,“加速度的变化率”的单位应是 $ \mathrm{m}/{\mathrm{s}}^{2} $
B.加速度的变化率保持为0的直线运动是速度均匀变化的直线运动
C.若加速度与速度同方向, $ a-t $ 图像如图所示,表示的是汽车的速度在减小
D.若加速度与速度同方向, $ a-t $ 图像如图所示,已知汽车在 $ t=0 $ 时速度为 $ 5\mathrm{m}/\mathrm{s} $ ,则 $ 2\mathrm{s} $ 末的速度大小为 $ 8\mathrm{m}/\mathrm{s} $
答案:BD
解析:变化率是变化量与所用时间的比值,“加速度的变化率”是 $ \dfrac{\mathrm{\Delta }a}{\mathrm{\Delta }t} $ , $ a $ 的单位是 $ \mathrm{m}/{\mathrm{s}}^{2} $ , $ t $ 的单位是 $ \mathrm{s} $ ,则 $ \dfrac{\mathrm{\Delta }a}{\mathrm{\Delta }t} $ 的单位为 $ \mathrm{m}/{\mathrm{s}}^{3} $ ,故 $ \mathrm{A} $ 错误;加速度的变化率为0是指加速度保持不变,即加速度恒定,做速度均匀变化的直线运动,故 $ \mathrm{B} $ 正确;若加速度与速度同方向,则汽车做加速运动,如题图所示,加速度减小,则汽车速度增加得越来越慢,但仍在加速,速度不会减小,故 $ \mathrm{C} $ 错误;根据题意可知在 $ a-t $ 图像中图像与时间轴所围图形的面积表示汽车速度的变化量,则 $ \mathrm{\Delta }v=\dfrac{1}{2}×2×3\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ ,由于加速度与速度同方向,故汽车做加速直线运动,已知初速度为 $ 5\mathrm{m}/\mathrm{s} $ ,则汽车在 $ 2\mathrm{s} $ 末的速度大小为 $ 8\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 正确.









 (多选)
(多选) (多选)
(多选)
 (多选)
(多选)