第一章素养检测
一、刷速度
1.下列说法正确的是( )
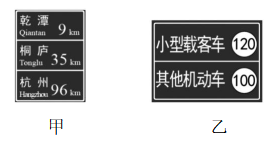
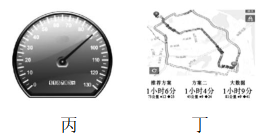
A.甲图是高速公路上的指示牌,上面的“ $ 96\mathrm{k}\mathrm{m} $ ”“ $ 35\mathrm{k}\mathrm{m} $ ”“ $ 9\mathrm{k}\mathrm{m} $ ”指的是位移
B.乙图是高速公路上的指示牌,上面的“120”“100”指的是平均速度的大小
C.丙图是汽车上的时速表,上面指针指示的“90”指90米每秒
D.丁图是导航中的信息,上面三个方案的位移相同
答案:D
解析:题图甲是高速公路上的指示牌,上面的“ $ 96\mathrm{k}\mathrm{m} $ ”“ $ 35\mathrm{k}\mathrm{m} $ ”“ $ 9\mathrm{k}\mathrm{m} $ ”指的是路程, $ \mathrm{A} $ 错误;题图乙是高速公路上的指示牌,上面的“120”“100”指的是瞬时速度的大小, $ \mathrm{B} $ 错误;题图丙是汽车上的时速表,上面指针指示的“90”指90千米每小时, $ \mathrm{C} $ 错误;题图丁是导航中的信息,上面三个方案的起点、终点一样,故位移相同, $ \mathrm{D} $ 正确.
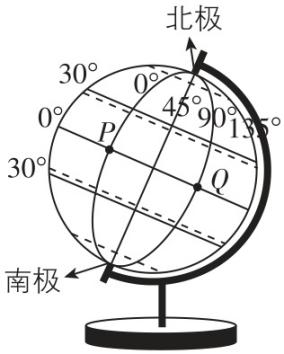
2.如图所示,半径为 $ R $ 的地球仪(可视为均匀球体)上, $ P $ 点为赤道与 $ {0}^{\circ } $ 经线的交点, $ Q $ 点为赤道与东经 $ {90}^{\circ } $ 经线的交点,一只蚂蚁从 $ P $ 点沿 $ {0}^{\circ } $ 经线向北爬行到北极点,然后又沿东经 $ {90}^{\circ } $ 经线向南爬行到 $ Q $ 点,则蚂蚁从 $ P $ 点运动到 $ Q $ 点的整个过程中的路程和位移大小分别为( )
A. $ 2\mathrm{\pi }R $ , $ 2R $
B. $ \mathrm{\pi }R $ , $ R $
C. $ \mathrm{\pi }R $ , $ \sqrt{2}R $
D. $ 2\mathrm{\pi }R $ , $ \sqrt{2}R $
答案:C
解析:将地球仪视为一个均匀的球体,蚂蚁从 $ P $ 点沿 $ {0}^{\circ } $ 经线向北爬行到北极点,路程恰好为四分之一圆周,即 $ {s}_{1}=\dfrac{1}{4}×2\mathrm{\pi }R=\dfrac{1}{2}\mathrm{\pi }R $ ,然后又沿东经 $ {90}^{\circ } $ 经线向南爬行到 $ Q $ 点,路程为 $ {s}_{2}=\dfrac{1}{4}×2\mathrm{\pi }R=\dfrac{1}{2}\mathrm{\pi }R $ ,整个过程中的路程为 $ s={s}_{1}+{s}_{2}=\mathrm{\pi }R $ ,从 $ P $ 点运动到 $ Q $ 点的整个过程位移大小等于 $ P $ 、 $ Q $ 两点间距离,由几何关系知 $ x=\sqrt{2}R $ ,故选 $ \mathrm{C} $ .
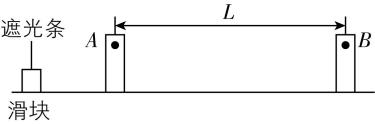
3.如图所示,在气垫导轨上安装有两个光电门 $ A $ 、 $ B $ , $ A $ 、 $ B $ 间的距离为 $ L=30\mathrm{c}\mathrm{m} $ .为了测量滑块的加速度,在滑块上安装了一宽度为 $ d=1\mathrm{c}\mathrm{m} $ 的遮光条,现让滑块以某一加速度通过光电门 $ A $ 、 $ B $ .记录了遮光条通过两光电门 $ A $ 、 $ B $ 的时间分别为 $ 0.010\mathrm{s} $ 、 $ 0.005\mathrm{s} $ ,滑块从光电门 $ A $ 到 $ B $ 的时间为 $ 0.200\mathrm{s} $ .则下列说法正确的是( )
A.滑块经过光电门 $ A $ 时的速度大小为 $ 1\mathrm{c}\mathrm{m}/\mathrm{s} $
B.滑块经过光电门 $ B $ 时的速度大小为 $ 2\mathrm{c}\mathrm{m}/\mathrm{s} $
C.滑块的加速度大小为 $ 5\mathrm{m}/{\mathrm{s}}^{2} $
D.滑块在光电门 $ A $ 、 $ B $ 间的平均速度大小为 $ 3\mathrm{m}/\mathrm{s} $
答案:C
解析:滑块经过光电门 $ A $ 时的速度大小为 $ {v}_{A}=\dfrac{0.01}{0.010}\mathrm{m}/\mathrm{s}=1\mathrm{m}/\mathrm{s} $ ,经过光电门 $ B $ 时的速度大小为 $ {v}_{B}=\dfrac{0.01}{0.005}\mathrm{m}/\mathrm{s}=2\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;滑块在光电门 $ A $ 、 $ B $ 间的平均速度大小为 $ \overline{v}=\dfrac{L}{{t}_{AB}}=\dfrac{0.30}{0.200}\mathrm{m}/\mathrm{s}=1.5\mathrm{m}/\mathrm{s} $ , $ \mathrm{D} $ 错误;滑块的加速度大小为 $ a=\dfrac{{v}_{B}-{v}_{A}}{{t}_{AB}}=5\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{C} $ 正确.
4.如图所示为某一公园的路线图,该图为一个半径为 $ R $ 的圆形,内部三角形为正三角形,圆心 $ O $ 恰好为正三角形的中心.小明和妈妈在晚上7:00进入公园大门,晚上7:15同时从公园 $ A $ 点出发,小明沿圆形轨迹 $ ABC $ 前进,在晚上8:00到达 $ C $ 点,妈妈沿直线 $ AB $ 运动到 $ B $ 点再沿直线 $ BC $ 到 $ C $ 点,用时35分钟.运动过程中小明和妈妈均可看成质点,则下列说法正确的是( )
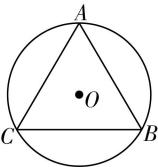
A.晚上7:00指的是时间间隔,晚上7:15指的是时刻
B.整个过程中,小明和妈妈的位移相同
C.整个过程中,小明和妈妈的平均速度相同
D.整个过程中,小明的平均速率大于妈妈的平均速率
答案:B
解析:晚上7:00和晚上7:15均指的是时刻,故 $ \mathrm{A} $ 错误;整个过程中,小明和妈妈的初位置均在 $ A $ 点,末位置均在 $ C $ 点,所以小明和妈妈的位移相同,根据 $ \overline{v}=\dfrac{x}{t} $ ,由于所用时间不相等,所以小明和妈妈的平均速度不相等,故 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;根据题意可知,整个过程中,小明的路程和所用时间分别为 $ {s}_{1}=\dfrac{2}{3}\cdot 2\mathrm{\pi }R=\dfrac{4\mathrm{\pi }R}{3} $ , $ {t}_{1}=45 \min $ ,妈妈的路程和所用时间分别为 $ {s}_{2}=4R \cos {30}^{\circ }=2\sqrt{3}R $ , $ {t}_{2}=35 \min $ ,则 $ {v}_{1}=\dfrac{{s}_{1}}{{t}_{1}} < {v}_{2}=\dfrac{{s}_{2}}{{t}_{2}} $ ,可知整个过程中,小明的平均速率小于妈妈的平均速率,故 $ \mathrm{D} $ 错误.
5. $ a $ 、 $ b $ 、 $ c $ 、 $ d $ 四个质点在一条直线上运动,它们的运动图像如图所示,下列说法不正确的是( )
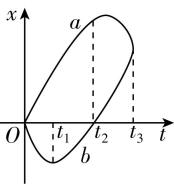
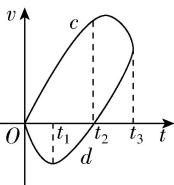
A. $ {t}_{1} $ 时刻质点 $ b $ 改变速度方向
B. $ {t}_{2} $ 时刻质点 $ d $ 改变速度方向
C.在 $ 0\sim {t}_{3} $ 时间内,质点 $ a $ 、 $ b $ 的平均速度相同
D.在 $ 0\sim {t}_{2} $ 时间内,质点 $ d $ 的位移先变大再变小
答案:D
解析:根据 $ x-t $ 图像的切线斜率表示速度可知,在 $ 0\sim {t}_{1} $ 时间内,质点 $ b $ 的速度为负,在 $ {t}_{1}\sim {t}_{2} $ 时间内,质点 $ b $ 的速度为正,即 $ {t}_{1} $ 时刻质点 $ b $ 改变速度方向, $ \mathrm{A} $ 正确; $ {t}_{2} $ 时刻质点 $ d $ 的速度由负值变为正值,故 $ {t}_{2} $ 时刻质点 $ d $ 改变速度方向, $ \mathrm{B} $ 正确;在 $ 0\mathrm{~}{t}_{3} $ 时间内, $ a $ 、 $ b $ 质点的初、末位置的差值相同,则位移相同,故平均速度相同, $ \mathrm{C} $ 正确;在 $ 0\sim {t}_{2} $ 时间内,质点 $ d $ 一直向负方向运动,其位移一直变大, $ \mathrm{D} $ 错误.本题选说法不正确的,故选 $ \mathrm{D} $ .
6.如图所示的 $ xOy $ 坐标系中,一质点从 $ O $ 点出发,沿 $ O-A-B $ 轨迹以不变的速率运动.已知 $ OA $ 段轨迹为直线, $ AB $ 段轨迹是以 $ O $ 为圆心、 $ OA $ 为半径的一段圆弧,则在质点沿 $ O-A-B $ 运动过程中( )
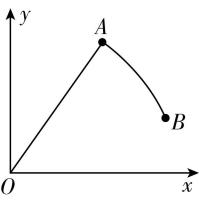
A.位移大小一直增大
B.平均速度大小先不变后减小
C.路程先增大后不变
D.平均速率一直增大
答案:B
解析:由题图可知,质点从 $ O $ 到 $ A $ 过程,位移一直增大,从 $ A $ 到 $ B $ 过程位移大小不变,故 $ \mathrm{A} $ 错误;根据 $ \overline{v}=\dfrac{s}{t} $ ,可知平均速度大小先不变后减小,故 $ \mathrm{B} $ 正确;路程是轨迹的长度,由题图可知质点的路程一直增大,故 $ \mathrm{C} $ 错误;依题意,质点的平均速率不变,故 $ \mathrm{D} $ 错误.
7. $ A $ 、 $ B $ 是一条平直公路上的两块路牌,一辆汽车由右向左经过 $ B $ 路牌时,一只小鸟恰好自 $ A $ 向 $ B $ 飞去,小鸟飞到汽车正上方立即折返,以原速率飞回 $ A $ ,一段时间后,汽车也行驶到 $ A $ .它们的位置与时间的关系如图所示,图中 $ {t}_{2}=2{t}_{1} $ ,由图可知( )
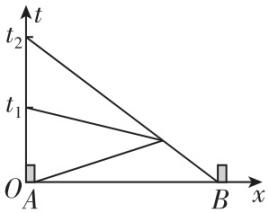
A.小鸟的速率是汽车的2倍
B.小鸟飞行的路程是汽车的3倍
C.相遇时小鸟与汽车的位移大小之比是 $ 3:1 $
D.小鸟和汽车在 $ 0\sim {t}_{2} $ 时间内位移相等
答案:C
解析:设 $ A $ 、 $ B $ 之间的距离为 $ L $ ,小鸟的速率为 $ {v}_{1} $ ,汽车的速率为 $ {v}_{2} $ , $ {t}_{2}=2{t}_{1} $ ,则小鸟从出发到与汽车相遇的时间和小鸟返回的时间相同,则它们相向运动的时间为 $ \dfrac{{t}_{1}}{2} $ ,则在小鸟和汽车相向运动的过程中有 $ {v}_{1}\cdot \dfrac{{t}_{1}}{2}+{v}_{2}\cdot \dfrac{{t}_{1}}{2}=L $ ,对于汽车有 $ {v}_{2}{t}_{2}=L $ ,又 $ {t}_{2}=2{t}_{1} $ ,联立可得 $ {v}_{1}=3{v}_{2} $ ,可知小鸟与汽车速度大小之比为 $ 3:1 $ ,故 $ \mathrm{A} $ 错误;根据 $ x=vt $ 可知从出发到相遇这段时间内,小鸟与汽车通过的位移大小之比等于速率之比,即为 $ 3:1 $ ,故 $ \mathrm{C} $ 正确;汽车通过的路程为 $ {x}_{2}={v}_{2}{t}_{2} $ ,小鸟通过的总路程为 $ {x}_{1}={v}_{1}{t}_{1}=3{v}_{2}\cdot \dfrac{{t}_{2}}{2}=\dfrac{3}{2}{v}_{2}{t}_{2}=\dfrac{3}{2}{x}_{2} $ ,可知小鸟与汽车通过的总路程之比为 $ 3:2 $ ,即小鸟飞行的总路程是汽车的1.5倍,故 $ \mathrm{B} $ 错误;小鸟最终回到出发点,故小鸟的位移为零,而汽车的位移不为零,故 $ \mathrm{D} $ 错误.
8.小天到同学家做客,发现他家的扫地机器人正在忙碌地工作着,机器人沿铺有相同大瓷砖的地面做加速度不变的直线运动,连续经过 $ P $ 、 $ Q $ 、 $ R $ 三点.在 $ PQ $ 段(2块砖)和 $ QR $ 段(3块砖)的平均速度分别为 $ 2{v}_{0} $ 和 $ {v}_{0} $ ,不计相邻瓷砖间的缝隙,则( )
 (多选)
(多选)
A.机器人经过 $ PQ $ 段与 $ QR $ 段所用时间之比为 $ 1:3 $
B.机器人在 $ PR $ 段的平均速度大小为 $ \dfrac{5}{4}{v}_{0} $
C.机器人在 $ PR $ 段的平均速度大小为 $ \dfrac{5}{3}{v}_{0} $
D.机器人通过每块砖过程中的速度变化量相同
答案:AB
解析:设每块瓷砖的长度为 $ d $ ,根据平均速度的定义可知,机器人经过 $ PQ $ 段和 $ QR $ 段所用时间之比为 $ {t}_{PQ}:{t}_{QR}=\dfrac{2d}{2{v}_{0}}:\dfrac{3d}{{v}_{0}}=1:3 $ , $ \mathrm{A} $ 正确;机器人在 $ PR $ 段的平均速度为 $ {\overline{v}}_{PR}=\dfrac{{x}_{PR}}{{t}_{PR}}=\dfrac{5d}{{t}_{PQ}+{t}_{QR}}=\dfrac{5d}{\dfrac{2d}{2{v}_{0}}+\dfrac{3d}{{v}_{0}}}=\dfrac{5}{4}{v}_{0} $ , $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;由加速度的定义可知 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ ,解得 $ \mathrm{\Delta }v=a\cdot \mathrm{\Delta }t $ ,尽管机器人的加速度不变,但机器人通过每块瓷砖的时间不同,故速度的变化量不同, $ \mathrm{D} $ 错误.
9.挥杆套马是我国蒙古族传统体育项目,如图甲.烈马从骑手身边奔驰而过时,骑手持 $ 6\mathrm{m} $ 长的套马杆,由静止开始催马追赶,二者的 $ v-t $ 图像如图乙所示,则( )
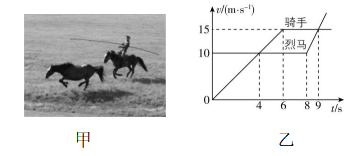 (多选)
(多选)
A. $ 0\sim 8\mathrm{s} $ 内烈马做匀速直线运动
B. $ 0\sim 6\mathrm{s} $ 内骑手做匀速直线运动
C. $ 4\sim 6\mathrm{s} $ 内骑手的加速度大小为 $ 7.5\mathrm{m}/{\mathrm{s}}^{2} $
D. $ 8\sim 9\mathrm{s} $ 内烈马的加速度大于 $ 0\sim 6\mathrm{s} $ 内骑手的加速度
答案:AD
解析: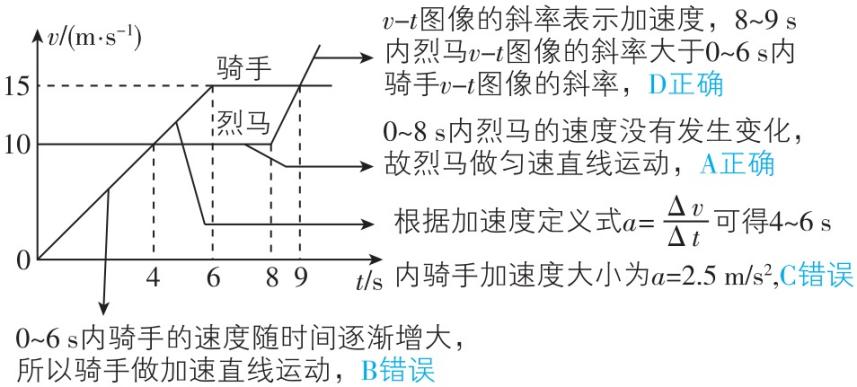
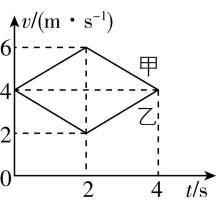
10.如图所示为甲、乙两辆玩具小车在一平直轨道上运动时的速度—时间图像,甲车先加速后减速,乙车先减速后加速.下列关于两辆车运动情况的说法中正确的是( )
 (多选)
(多选)
A.甲车加速和减速时的加速度大小均为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $
B.若两辆车在 $ t=0 $ 时刻从同一位置出发,则在 $ t=2\mathrm{s} $ 时两者相距最远
C.若两辆车在 $ t=0 $ 时刻从同一位置出发,则在 $ t=4\mathrm{s} $ 时两者相距最远
D.在 $ 0\sim 4\mathrm{s} $ 内甲车的平均速度比乙车的平均速度大 $ 4\mathrm{m}/\mathrm{s} $
答案:AC
解析: $ v-t $ 图像斜率的绝对值表示加速度的大小,甲车加速和减速时的加速度大小均为 $ a=\dfrac{6-4}{2}\mathrm{m}/{\mathrm{s}}^{2}=1\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{A} $ 正确;若两辆车在 $ t=0 $ 时刻从同一位置出发, $ 0\sim 4\mathrm{s} $ 内甲车的速度始终不小于乙车的速度,则两车在 $ t=4\mathrm{s} $ 时相距最远,故 $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确;由题图可知,在 $ 0\sim 4\mathrm{s} $ 内,两车的速度之差最大为 $ 4\mathrm{m}/\mathrm{s} $ ,故两车平均速度的差值小于 $ 4\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 错误.
11.(10分)小明为了测定气垫导轨上滑块的加速度,在滑块上安装了宽度为 $ d=3.0\mathrm{c}\mathrm{m} $ 的遮光条,如图所示,滑块在牵引力作用下先后通过两个光电门,配套的数字计时器记录了遮光条通过光电门1的时间为 $ \mathrm{\Delta }{t}_{1}=0.30\mathrm{s} $ ,通过光电门2的时间为 $ \mathrm{\Delta }{t}_{2}=0.10\mathrm{s} $ ,遮光条从开始遮住光电门1到开始遮住光电门2的时间为 $ \mathrm{\Delta }t=3.0\mathrm{s} $ .
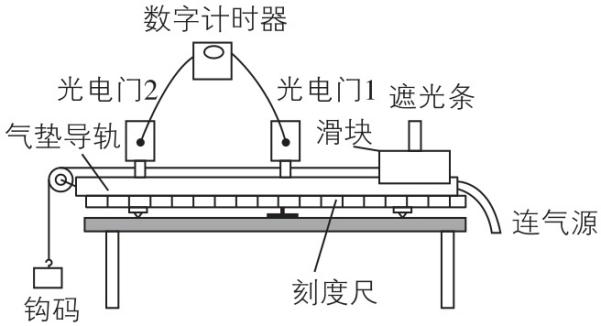
(1) 滑块通过光电门1时的速度大小 $ {v}_{1}= $ $ \mathrm{m}/\mathrm{s} $ ,滑块通过光电门2时的速度大小 $ {v}_{2}= $ $ \mathrm{m}/\mathrm{s} $ .若该过程加速度不变,则滑块的加速度大小 $ a= $ $ \mathrm{m}/{\mathrm{s}}^{2} $ .(所有结果均保留两位有效数字)
(2) 由此测得的瞬时速度 $ {v}_{1} $ 和 $ {v}_{2} $ 只是一个近似值,它们实质上是通过光电门1和2时的 ,要使瞬时速度的测量值更接近于真实值,可将遮光条的 减小一些.
答案:(1) 0.10;0.30;0.067
(2) 平均速度;宽度
解析:(1) 根据极短时间内的平均速度表示瞬时速度可知, $ {v}_{1}=\dfrac{d}{\mathrm{\Delta }{t}_{1}}=\dfrac{0.03}{0.30}\mathrm{m}/\mathrm{s}=0.10\mathrm{m}/\mathrm{s} $ , $ {v}_{2}=\dfrac{d}{\mathrm{\Delta }{t}_{2}}=\dfrac{0.03}{0.10}\mathrm{m}/\mathrm{s}=0.30\mathrm{m}/\mathrm{s} $ ,根据加速度定义式有 $ a=\dfrac{{v}_{2}-{v}_{1}}{\mathrm{\Delta }t}=\dfrac{0.30-0.10}{3.0}\mathrm{m}/{\mathrm{s}}^{2}=0.067\mathrm{m}/{\mathrm{s}}^{2} $ ;
(2) $ {v}_{1} $ 和 $ {v}_{2} $ 实质上是遮光条通过光电门1和2时的平均速度,要使瞬时速度的测量值更接近于真实值,可将遮光条的宽度减小一些.
12.(12分)学校操场跑道的平面示意图如图所示,该跑道由两个半圆跑道和两个直线跑道组成,已知直线跑道 $ BC=AD=100\mathrm{m} $ ,每个半圆跑道的弧长也为 $ 100\mathrm{m} $ .某次学校举办运动会,甲、乙、丙三位同学(均视为质点)分别参加了 $ 100\mathrm{m} $ 、 $ 200\mathrm{m} $ 和 $ 800\mathrm{m} $ 赛跑,三位同学参加比赛时均以 $ A $ 点为起跑点,均沿逆时针方向跑动,最终获得的成绩分别为 $ 12.5\mathrm{s} $ 、 $ 27\mathrm{s} $ 和 $ 180\mathrm{s} $ ,求:
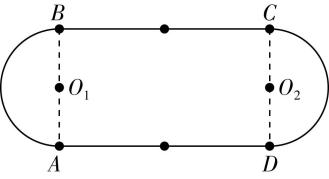
(1) 甲同学参加 $ 100\mathrm{m} $ 赛跑的平均速度大小;
(2) 乙同学参加 $ 200\mathrm{m} $ 赛跑的位移大小(计算结果可保留 $ \mathrm{\pi } $ 和根号);
(3) 丙同学参加 $ 800\mathrm{m} $ 赛跑的平均速度大小.
答案:(1) $ 8\mathrm{m}/\mathrm{s} $
(2) $ 100\sqrt{1+\dfrac{4}{{\mathrm{\pi }}^{2}}}\mathrm{m} $
(3) 0
解析:(1) 甲同学参加 $ 100\mathrm{m} $ 赛跑过程中沿直线运动,则位移大小为 $ {x}_{1}=100\mathrm{m} $ ,用时 $ {t}_{1}=12.5\mathrm{s} $ ,则平均速度大小为 $ {v}_{1}=\dfrac{{x}_{1}}{{t}_{1}}=8\mathrm{m}/\mathrm{s} $ .
(2) 乙同学参加 $ 200\mathrm{m} $ 赛跑的终点为 $ C $ 点,则位移大小为 $ A $ 、 $ C $ 之间的距离,根据几何关系可知位移大小为 $ {x}_{2}=\sqrt{{\left(AD\right) ^ {2}}+{\left(2\dfrac{\stackrel{⌢}{CD}}{\mathrm{\pi }}\right) ^ {2}}}=100\sqrt{1+\dfrac{4}{{\mathrm{\pi }}^{2}}}\mathrm{m} $ .
(3) 丙同学参加 $ 800\mathrm{m} $ 赛跑,终点和起点位置相同,则位移为零,平均速度为零.
13.(18分)巡警驾驶一辆警车在一段平直的高速公路上以某一速度巡航,他想知道车内速度仪表指示的速度是否准确.当他准备穿越公路正前方高山悬崖下的隧道时,他通过车载超声波系统向前方发射了两个超声波脉冲,超声波系统显示的图形如图所示,其中 $ A $ 为发射的超声波脉冲, $ B $ 为接收到的超声波脉冲.已知一个超声波脉冲持续的时间很短,声音在空气中的传播速度为 $ 336\mathrm{m}/\mathrm{s} $ .求:
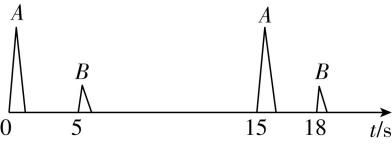
(1) 警车行驶的速度 $ {v}_{1} $ .
(2) 山崖第一次反射超声波的时刻 $ t $ .(保留4位有效数字)
答案:(1) $ 24\mathrm{m}/\mathrm{s} $
(2) $ 2.679\mathrm{s} $
解析:(1) 由题图知, $ {t}_{0}=0 $ 时刻,警车第一次发射超声波脉冲,经 $ {t}_{1}=5\mathrm{s} $ 接收到返回的超声波信号,又经过 $ \mathrm{\Delta }t=10\mathrm{s} $ ,第二次发射超声波脉冲,经 $ {t}_{2}=3\mathrm{s} $ 接收到返回的超声波信号.设警车行驶速度为 $ {v}_{1} $ ,空气中声速 $ {v}_{2}=336\mathrm{m}/\mathrm{s} $ ,第一次发射超声波脉冲时警车与隧道口的距离为 $ {x}_{1} $ ,第二次发射超声波脉冲时警车与隧道口的距离为 $ {x}_{2} $ ,则 $ 2{x}_{1}-{v}_{1}{t}_{1}={v}_{2}{t}_{1} $ , $ 2{x}_{2}-{v}_{1}{t}_{2}={v}_{2}{t}_{2} $ ,又 $ {x}_{1}-{x}_{2}={v}_{1}(\mathrm{\Delta }t+{t}_{1}) $ ,联立解得 $ {v}_{1}=24\mathrm{m}/\mathrm{s} $ .
(2) 由(1)问分析得 $ {x}_{1}=900\mathrm{m} $ ,山崖第一次反射超声波的时刻 $ t=\dfrac{{x}_{1}}{{v}_{2}}\approx 2.679\mathrm{s} $ .









 (多选)
(多选) (多选)
(多选)
 (多选)
(多选)

