第1节 实验：探究小车速度随时间变化的规律

一、刷基础

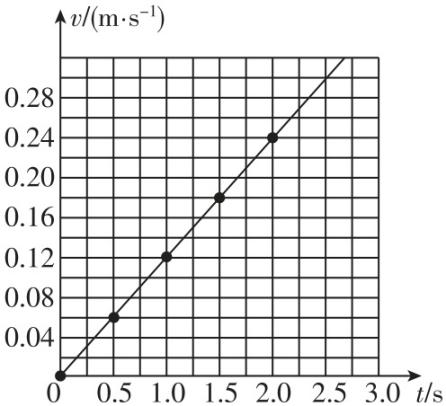
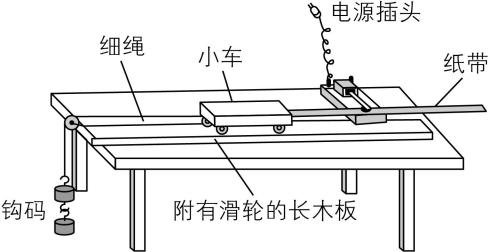
1．在“测定匀变速直线运动的加速度”的实验中：

试题资源网 https://stzy.com

（1） 打点计时器是利用  （填“直流”或“交流”）电源进行计时的仪器，若电源频率为 $ 50\mathrm{H}\mathrm{z} $ ，则每隔  秒打一个点，其中电火花计时器所用电压为  伏；

（2） 除打点计时器、小车、一端附有滑轮的长木板、细绳、钩码、导线及开关外，在下面的实验器材中，必须使用的有    ；（填选项代号）

A．电压合适的交流电源B．电压可调的直流电源

C．刻度尺D．停表

E．天平

（3） 实验过程中，下列做法正确的是    .

A．先释放小车，再接通电源

B．先接通电源，再释放小车

C．将接好纸带的小车停在靠近长木板滑轮处

D．将接好纸带的小车停在靠近打点计时器处

答案：

（1） 交流；0.02；220

（2） AC

（3） BD

解析：

（1） 打点计时器是利用交流电源进行计时的仪器.若电源频率为 $ 50\mathrm{H}\mathrm{z} $ ,则每隔 $ T=\dfrac{1}{f}=\dfrac{1}{50}\mathrm{s}=0.02\mathrm{s} $ 打一个点.电火花计时器所用电压为220伏.

（2） 必须使用的有电压合适的交流电源,使打点计时器能正常工作, $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误；需要测量纸带上计数点间的距离,因此必须使用刻度尺, $ \mathrm{C} $ 正确；打点计时器记录了时间,因此不需要停表, $ \mathrm{D} $ 错误；不需要测量钩码和小车的质量,因此不需要天平, $ \mathrm{E} $ 错误.

（3） 先释放小车,再接通电源,这样在纸带上会打出很少的点,纸带的利用率很低,会产生较大的实验误差, $ \mathrm{A} $ 错误；将接好纸带的小车停在靠近打点计时器处,先接通电源,待打点计时器打点稳定后,再释放小车,纸带会得到充分利用,纸带上会得到更多的数据,以减小实验误差, $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确；将接好纸带的小车停在靠近长木板滑轮处,纸带上会打出很少的点,会增大实验误差, $ \mathrm{C} $ 错误.

2．某同学在做“研究匀变速直线运动”的实验中，打点计时器所接电源的频率为 $ 50\mathrm{H}\mathrm{z} $ ，实验时得到表示小车运动过程的一条清晰纸带如图所示，纸带上相邻两计数点间还有4个计时点没有画出，测得相邻计数点间距离分别为 $ {s}_{1} $ 、 $ {s}_{2} $ 、 $ {s}_{3} $ 、 $ {s}_{4} $ 、 $ {s}_{5} $ 、 $ {s}_{6} $ ，回答下列问题：

试题资源网 https://stzy.com

（1） 打点计时器使用  （填“交流”或“直流”）电源；

（2） 相邻两计数点间的时间间隔 $ T= $         ；

（3） 3点处瞬时速度表达式为 $ {v}_{3}= $             （用题中所给物理量符号表示）；

（4） 下列关于打点计时器使用的说法中，正确的是    .

A．电火花计时器使用的是 $ 8\mathrm{V} $ 交流电源

B．先释放纸带，后接通打点计时器的电源

C．纸带上打的点越密，说明小车运动得越快

D．如果实际电源频率为 $ 55\mathrm{H}\mathrm{z} $ ，而计算时仍按 $ 50\mathrm{H}\mathrm{z} $ 计算，则速度的测量值偏小

答案：

（1） 交流

（2） $ 0.1\mathrm{s} $

（3） $ \dfrac{{s}_{3}+{s}_{4}}{2T} $

（4） D

解析：

（1） 打点计时器使用交流电源.

（2） 打点计时器所接电源的频率为 $ 50\mathrm{H}\mathrm{z} $ ,纸带上相邻两计数点间还有4个计时点没有画出,则相邻两计数点间时间间隔 $ T=\dfrac{1}{f}×5=0.02×5\mathrm{s}=0.1\mathrm{s} $ .

（3） 利用平均速度表示中间时刻的瞬时速度,可得3点处瞬时速度表达式为 $ {v}_{3}=\dfrac{{s}_{3}+{s}_{4}}{2T} $ .

（4） 电火花计时器使用的是 $ 220\mathrm{V} $ 交流电源, $ \mathrm{A} $ 错误；为了充分利用纸带,得到更多的数据,应先接通打点计时器的电源,待打点稳定后,再释放纸带, $ \mathrm{B} $ 错误；纸带上打的点越密,说明小车在相同时间内运动的距离越小,则小车运动得越慢, $ \mathrm{C} $ 错误；用打点计时器测定小车的速度,如果实际电源频率为 $ 55\mathrm{H}\mathrm{z} $ ,可知打点周期 $ T\prime =\dfrac{1}{55}\mathrm{s} < \dfrac{1}{50}\mathrm{s} $ ,而计算时仍按 $ 50\mathrm{H}\mathrm{z} $ 计算,计算时所用时间偏大,则速度的测量值偏小, $ \mathrm{D} $ 正确.

3．在研究匀变速直线运动的实验中，已算出小车经过各计数点的瞬时速度，则为了计算加速度，最佳的方法是（      ）

A．根据任意两计数点的速度用公式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 算出加速度

B．依次算出通过连续两计数点间的加速度，算出平均值作为小车的加速度

C．根据实验数据画出 $ v-t $ 图像，量取其倾角 $ \theta $ ，用 $ a= \tan \theta $ 求出加速度

D．根据实验数据画出 $ v-t $ 图像，由图像上相距较远的两点所对应的速度、时间用公式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 算出加速度

答案：D
解析：

根据任意两计数点的速度用公式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 算出加速度,只选用了两个数据,误差较大,不是最佳方法,故 $ \mathrm{A} $ 不符合题意；依次算出通过连续两计数点间的加速度,算出平均值作为小车的加速度,此方法计算数据较多，且部分数据偏差较大，不是最佳方法,故 $ \mathrm{B} $ 不符合题意；根据实验数据画出 $ v-t $ 图像,由图像上相距较远的两点所对应的速度、时间用公式 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t} $ 算出加速度,充分利用了数据,误差较小,是最佳方法,但不能量取图线的倾角 $ \theta $ ,用 $ a= \tan \theta $ 求出加速度,因为 $ v $ 轴和 $ t $ 轴所选标度不一定相同, $ \tan \theta $ 不一定等于图线的斜率,故 $ \mathrm{C} $ 不符合题意, $ \mathrm{D} $ 符合题意.

4．结合“探究小车速度随时间变化的规律”的实验（装置如图甲），回答下列问题：

试题资源网 https://stzy.com

甲

（1） 如图乙，刻度尺的0刻度线与“0”点对齐，测量点“4”到“0”点的距离为     $ \mathrm{c}\mathrm{m} $ ；该同学已将1、2、3、4点对应时刻的瞬时速度进行计算填入表中，请你将打下测量点“5”对应时刻的瞬时速度填入表中（结果保留三位有效数字）；请你把“5”的数据补充到图丙中，并拟合图线.

试题资源网 https://stzy.com试题资源网 https://stzy.com

测量点

1

2

3

4

5

瞬时速度 $ (\mathrm{m}\cdot {\mathrm{s}}^{-1}) $

0.501

0.520

0.525

0.540

    

（2） 根据拟合好的图像求出小车的加速度大小为 $ a= $      $ \mathrm{m}/{\mathrm{s}}^{2} $ .（结果保留三位有效数字）

（3） 关于该实验，下列说法正确的是.

A．重复实验时，可以增加悬挂的槽码，也可以在小车里增加重物

B．实验时，牵引小车的细绳必须平行于长木板，而且长木板也必须水平放置

C．若实验时电源频率略低于 $ 50\mathrm{H}\mathrm{z} $ ，但该同学并不知道，则小车速度测量值将大于实际值

D．如果实验用电火花计时器，实验时所用的电源电压略低于 $ 220\mathrm{V} $ ，则加速度的测量值将小于实际值

答案：

（1） 19.90；0.550；如图所示

试题资源网 https://stzy.com

（2） 0.120

（3） AC

解析：

（1） 由题图乙可知,刻度尺的0刻度线与“0”点对齐,测量点“4”到“0”点的距离为 $ 19.90\mathrm{c}\mathrm{m} $ .打下测量点“5”对应时刻的瞬时速度为 $ {v}_{5}=\dfrac{\mathrm{\Delta }{x}_{46}}{\mathrm{\Delta }t}=\dfrac{30.9-19.9}{10×0.02}×{10}^{-2}\mathrm{m}/\mathrm{s}=0.550\mathrm{m}/\mathrm{s} $ .在题图丙中补点并拟合图线,如图所示.

试题资源网 https://stzy.com

（2） 由图像可得 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\dfrac{0.550-0.490}{0.5}\mathrm{m}/{\mathrm{s}}^{2}=0.120\mathrm{m}/{\mathrm{s}}^{2} $ .

（3） 重复实验时,可以增加悬挂的槽码,也可以在小车里增加重物,以此来改变小车的速度和加速度, $ \mathrm{A} $ 正确；实验时,牵引小车的细绳必须平行于长木板,长木板水平放置或倾斜放置均可,只要小车能做加速运动即可, $ \mathrm{B} $ 错误；若实验时电源频率略低于 $ 50\mathrm{H}\mathrm{z} $ ,可知打点周期 $ T=\dfrac{1}{f} $ 变大,但该同学并不知道,仍按 $ 0.02\mathrm{s} $ 计算,则小车速度测量值将大于实际值, $ \mathrm{C} $ 正确；如果实验用电火花计时器,实验时的电压略低于 $ 220\mathrm{V} $ ,但是电源的频率不变,则打点周期不变,则加速度的测量值等于实际值, $ \mathrm{D} $ 错误.

5．一小球在桌面上从静止开始做加速直线运动，现用高速摄影机在同一底片上多次曝光，记录下小球每次曝光的位置，并将小球的位置编号.如图甲所示，1位置恰为小球刚开始运动的瞬间，作为零时刻.摄影机连续两次曝光的时间间隔均相同.

试题资源网 https://stzy.com

甲

（1） 小球从1位置到6位置的运动过程中经过各位置的速度如表所示，将表中的数据补充完整.

计数点序号

1

2

3

4

5

速度 $ {v}_{n}/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $

$ {v}_{1}=0 $

$ {v}_{2}=0.06 $

$ {v}_{3}= $   

$ {v}_{4}=0.18 $

$ {v}_{5}= $   

（2） 在图乙所示的坐标纸上作出小球的速度—时间图像（保留描点痕迹）.

试题资源网 https://stzy.com

乙

（3） 由 $ v-t $ 图像可知小球运动的规律：速度随时间        .

答案：

（1） 0.12；0.24

（2） 见解析图

（3） 均匀增加

解析：

（1） $ {x}_{1}+{x}_{2}=0.060\mathrm{m} $ ,且 $ {v}_{2}=\dfrac{{x}_{1}+{x}_{2}}{2T}\mathrm{m}/\mathrm{s}=0.06\mathrm{m}/\mathrm{s} $ ,所以 $ T=0.5\mathrm{s} $ . $ {x}_{2}+{x}_{3}=0.120\mathrm{m} $ ,则 $ {v}_{3}=\dfrac{{x}_{2}+{x}_{3}}{2T}=\dfrac{0.120}{2×0.5}\mathrm{m}/\mathrm{s}=0.12\mathrm{m}/\mathrm{s}.{x}_{4}+{x}_{5}=0.240\mathrm{m} $ ,则 $ {v}_{5}=\dfrac{{x}_{4}+{x}_{5}}{2T}=\dfrac{0.240}{2×0.5}\mathrm{m}/\mathrm{s}=0.24\mathrm{m}/\mathrm{s} $ .

（2） $ v-t $ 图像如图所示.试题资源网 https://stzy.com

（3） 小球运动的 $ v-t $ 图像是一条斜向上的直线,表示小球的速度随时间均匀增加.

6．在“探究小车速度随时间变化的规律”实验中，打点计时器接在低压交流电源上，电源频率为 $ 50\mathrm{H}\mathrm{z} $ ，某同学在打出的纸带上共取了 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 、 $ E $ 、 $ F $ 六个计数点（每相邻两个计数点间有四个点未画出），如图甲所示.从每一个计数点处将纸带剪开分成五段（分别为 $ a $ 、 $ b $ 、 $ c $ 、 $ d $ 、 $ e $ 段），将这五段纸带由短到长紧靠但不重叠地粘在 $ xOy $ 坐标系中，如图乙.

试题资源网 https://stzy.com

（1） 若在图乙 $ xOy $ 坐标系中用最简洁的方法作出能表示 $ v-t $ 关系的图线，其中    轴相当于 $ v $ 轴，    轴相当于 $ t $ 轴.（均填“ $ x $ ”或“ $ y $ ”）

（2） 从计数点 $ A $ 开始计时，为求出 $ t=0.15\mathrm{s} $ 时刻的瞬时速度，需要测出    段纸带的长度.

（3） 若测得 $ a $ 段纸带的长度为 $ 2.0\mathrm{c}\mathrm{m} $ ， $ e $ 段纸带的长度为 $ 10.0\mathrm{c}\mathrm{m} $ ，则可求出加速度的大小为     $ \mathrm{m}/{\mathrm{s}}^{2} $ .

答案：

（1） $ y $ ； $ x $

（2） $ b $

（3） 2

解析：

（1） 由题意可知相邻计数点间的时间间隔相等,利用平均速度等于中间时刻的瞬时速度,可知剪下的每一段纸带的中间时刻速度与纸带的长度成正比,若在题图乙 $ xOy $ 坐标系中用最简洁的方法作出能表示 $ v-t $ 关系的图线,则 $ y $ 轴相当于 $ v $ 轴, $ x $ 轴相当于 $ t $ 轴.

（2） 每相邻两个计数点间有四个点未画出,可知相邻计数点间的时间间隔为 $ T=5×0.02\mathrm{s}=0.1\mathrm{s} $ ,从计数点 $ A $ 开始计时, $ t=0.15\mathrm{s} $ 时刻为 $ BC $ 段的中间时刻,利用平均速度表示中间时刻的瞬时速度（本章第3节学习）,可知为求出 $ t=0.15\mathrm{s} $ 时刻的瞬时速度,需要测出 $ b $ 段纸带的长度.

（3） 若测得 $ a $ 段纸带的长度为 $ 2.0\mathrm{c}\mathrm{m} $ , $ e $ 段纸带的长度为 $ 10.0\mathrm{c}\mathrm{m} $ ,从计数点 $ A $ 开始计时,则有 $ {v}_{0.05}=\dfrac{2.0×{10}^{-2}}{0.1}\mathrm{m}/\mathrm{s}=0.2\mathrm{m}/\mathrm{s} $ , $ {v}_{0.45}=\dfrac{10.0×{10}^{-2}}{0.1}\mathrm{m}/\mathrm{s}=1.0\mathrm{m}/\mathrm{s} $ ,则加速度的大小为 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\dfrac{1.0-0.2}{0.45-0.05}\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ .