第2节 匀变速直线运动的速度与时间的关系
一、刷基础
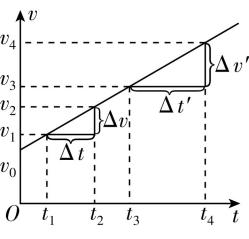
1.关于匀变速直线运动,下列说法正确的是( )
 (多选)
(多选)
A. $ v-t $ 图像是一条倾斜的直线
B.物体运动的加速度可以变化
C.无论 $ \mathrm{\Delta }t $ 选在什么区间,对应的速度的变化量 $ \mathrm{\Delta }v $ 与所用的时间 $ \mathrm{\Delta }t $ 之比都是一样的
D.在匀变速直线运动中,如果物体的速度随时间均匀减小,这种运动叫作匀加速直线运动
答案:AC
解析: $ v-t $ 图像的切线斜率表示加速度,由于匀变速直线运动的加速度保持不变,所以匀变速直线运动的 $ v-t $ 图像是一条倾斜的直线,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;根据 $ \mathrm{\Delta }v=a\mathrm{\Delta }t $ ,由于加速度保持不变,无论 $ \mathrm{\Delta }t $ 选在什么区间,对应的速度的变化量 $ \mathrm{\Delta }v $ 与所用的时间 $ \mathrm{\Delta }t $ 之比都是一样的,故 $ \mathrm{C} $ 正确;在匀变速直线运动中,如果物体的速度随时间均匀减小,这种运动叫作匀减速直线运动,故 $ \mathrm{D} $ 错误.
2.汽车在高速公路以 $ 25\mathrm{m}/\mathrm{s} $ 的速度行驶,某时刻想要超越前方车辆,开始以 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度做匀加速直线运动,则汽车在第 $ 3\mathrm{s} $ 末的速度是( )
A. $ 27\mathrm{m}/\mathrm{s} $
B. $ 28\mathrm{m}/\mathrm{s} $
C. $ 30\mathrm{m}/\mathrm{s} $
D. $ 31\mathrm{m}/\mathrm{s} $
答案:D
解析:汽车做匀加速直线运动,在第 $ 3\mathrm{s} $ 末的速度 $ v={v}_{0}+at=25\mathrm{m}/\mathrm{s}+2\mathrm{m}/{\mathrm{s}}^{2}×3\mathrm{s}=31\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 正确.
3.若火箭发射过程中某段时间内火箭速度的变化规律为 $ v=(2t+4)\mathrm{m}/\mathrm{s} $ ,这段时间内( )
A.火箭的初速度为 $ 2\mathrm{m}/\mathrm{s} $
B.火箭的加速度为 $ 4\mathrm{m}/{\mathrm{s}}^{2} $
C.在 $ 3\mathrm{s} $ 末,火箭的瞬时速度为 $ 10\mathrm{m}/\mathrm{s} $
D.火箭做匀减速直线运动
答案:C
解析:根据 $ v=(2t+4)\mathrm{m}/\mathrm{s} $ 可知火箭的初速度 $ {v}_{0}=4\mathrm{m}/\mathrm{s} $ ,加速度 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,则火箭做匀加速直线运动, $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误;在 $ 3\mathrm{s} $ 末,火箭的瞬时速度为 $ v=(2×3+4)\mathrm{m}/\mathrm{s}=10\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确.
4.滑雪运动员以加速度 $ {a}_{1} $ 由静止从坡顶沿直线匀加速滑下,测得 $ {t}_{1}=20\mathrm{s} $ 时的速度为 $ 20\mathrm{m}/\mathrm{s} $ , $ {t}_{2}=50\mathrm{s} $ 时到达坡底,又以加速度 $ {a}_{2} $ 沿水平面匀减速运动 $ {t}_{3}=25\mathrm{s} $ 后停止.运动员到达坡底即将沿水平面运动时速度大小不变,求:
(1) $ {a}_{1} $ 和 $ {a}_{2} $ 的大小;
(2) 到达坡底后再经过 $ {t}_{4}=26\mathrm{s} $ 时的速度大小.
答案:(1) $ 1\mathrm{m}/{\mathrm{s}}^{2} $ ; $ 2\mathrm{m}/{\mathrm{s}}^{2} $
(2) 0
解析:(1) 滑雪运动员以加速度 $ {a}_{1} $ 由静止从坡顶沿直线匀加速滑下,由速度—时间公式可得 $ {v}_{1}={a}_{1}{t}_{1} $ ,代入数据解得 $ {a}_{1}=1\mathrm{m}/{\mathrm{s}}^{2} $ , $ {t}_{2}=50\mathrm{s} $ 时到达坡底,此时运动员的速度 $ {v}_{2}={a}_{1}{t}_{2}=1×50\mathrm{m}/\mathrm{s}=50\mathrm{m}/\mathrm{s} $ ,在水平面做匀减速运动时,以运动员的方向为正方向,滑雪运动员以加速度 $ {a}_{2} $ 匀减速过程有 $ 0-{v}_{2}={a}_{2}{t}_{3} $ ,代入数据解得 $ {a}_{2}=\dfrac{-50}{25}\mathrm{m}/{\mathrm{s}}^{2}=-2\mathrm{m}/{\mathrm{s}}^{2} $ ,则加速度大小为 $ 2\mathrm{m}/{\mathrm{s}}^{2} $ .
(2) 由题意知,运动员到达坡底后再运动 $ 25\mathrm{s} $ 速度减为0,故运动员到达坡底后再经过 $ {t}_{4}=26\mathrm{s} $ 时的速度大小为0.
5.某小组自制一枚土火箭,设火箭由地面竖直向上发射,取向上为正方向.从火箭升空后某时刻开始计时, $ v-t $ 图像如图所示,由图像可知( )
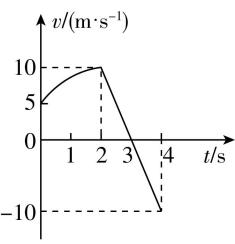
A. $ 0\sim 2\mathrm{s} $ 内火箭做匀加速运动
B. $ 2\sim 4\mathrm{s} $ 内火箭的加速度大小为 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,方向在 $ t=3\mathrm{s} $ 时改变
C. $ 0\sim 2\mathrm{s} $ 内火箭上升, $ t=2\mathrm{s} $ 时火箭开始下落
D. $ t=3\mathrm{s} $ 时火箭离地面最远
答案:D
解析:由题图可知 $ 0\sim 2\mathrm{s} $ 内火箭速度增大,但是 $ v-t $ 图像为曲线,火箭做变加速运动, $ \mathrm{A} $ 错误;根据图像的斜率为加速度可知, $ 2\sim 4\mathrm{s} $ 内火箭的加速度大小为 $ a=|\dfrac{-10-10}{4-2}|\mathrm{m}/{\mathrm{s}}^{2}=10\mathrm{m}/{\mathrm{s}}^{2} $ ,加速度方向在 $ t=3\mathrm{s} $ 时没有改变, $ \mathrm{B} $ 错误;由题图可知, $ t=3\mathrm{s} $ 时火箭速度反向,开始下落, $ \mathrm{C} $ 错误;火箭上升到最高点时离地面最远,在最高点时速度为零,所以 $ t=3\mathrm{s} $ 时火箭离地面最远, $ \mathrm{D} $ 正确.
6.给滑块一初速度 $ {v}_{0} $ ,使它沿光滑斜面向上做匀变速运动,加速度大小为 $ a $ ,当滑块速度大小变为 $ \dfrac{{v}_{0}}{2} $ 时,所用时间可能是( )(多选)
A. $ \dfrac{{v}_{0}}{4a} $
B. $ \dfrac{{v}_{0}}{2a} $
C. $ \dfrac{3{v}_{0}}{2a} $
D. $ \dfrac{3{v}_{0}}{a} $
答案:BC
解析:以滑块初速度方向为正方向,若末速度与初速度方向相同,则 $ \dfrac{{v}_{0}}{2}={v}_{0}-a{t}_{1} $ ,得 $ {t}_{1}=\dfrac{{v}_{0}}{2a} $ ,若末速度与初速度方向相反,有 $ -\dfrac{{v}_{0}}{2}={v}_{0}-a{t}_{2} $ ,得 $ {t}_{2}=\dfrac{3{v}_{0}}{2a} $ ,故 $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确.
7.飞机着陆后以 $ 6\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度做匀减速直线运动,若其着陆时的速度大小为 $ 60\mathrm{m}/\mathrm{s} $ ,则它着陆后 $ 12\mathrm{s} $ 末的速度为( )
A. $ 12\mathrm{m}/\mathrm{s} $
B. $ 12\mathrm{m}/\mathrm{s} $
C. $ 132\mathrm{m}/\mathrm{s} $
D.0
答案:D
解析:规定着陆时的速度方向为正方向,飞机着陆时的速度 $ {v}_{0}=60\mathrm{m}/\mathrm{s} $ ,加速度 $ a=-6\mathrm{m}/{\mathrm{s}}^{2} $ ,则飞机速度减到零所用的时间为 $ t=\dfrac{0-60}{-6}\mathrm{s}=10\mathrm{s} $ ,可知飞机在着陆后 $ 10\mathrm{s} $ 时停下,则飞机着陆后 $ 12\mathrm{s} $ 末的速度为0,故 $ \mathrm{D} $ 正确.
二、刷提升
1.如图所示,某无人机从地面由静止开始竖直上升,先做匀加速直线运动,紧接着做匀减速直线运动,减速到0后悬停在空中.加速时加速度大小为 $ {a}_{1} $ ,减速时加速度大小为 $ {a}_{2} $ .若无人机在该过程中运动的总时间为 $ t $ ,则无人机减速运动的时间为( )

A. $ \dfrac{{a}_{1}}{{a}_{1}+{a}_{2}}t $
B. $ \dfrac{{a}_{2}}{{a}_{1}+{a}_{2}}t $
C. $ \dfrac{{a}_{2}}{{a}_{1}}t $
D. $ \dfrac{{a}_{1}}{{a}_{2}}t $
答案:A
解析:设无人机做匀减速运动的时间为 $ {t}_{2} $ ,根据题意得 $ {a}_{1}(t-{t}_{2})={a}_{2}{t}_{2} $ ,解得 $ {t}_{2}=\dfrac{{a}_{1}}{{a}_{1}+{a}_{2}}t $ , $ \mathrm{A} $ 正确.
2.一辆可视为质点的汽车在平直公路上运动的速度—时间关系图像如图所示,整个运动过程中加速度的大小始终为 $ a $ ,下列说法正确的是( )
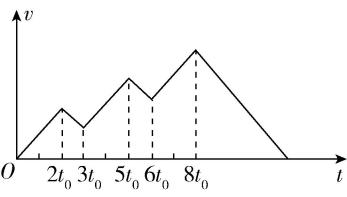
A. $ 2{t}_{0} $ 至 $ 3{t}_{0} $ 时间内汽车速度的变化量为 $ 2a{t}_{0} $
B.汽车的最大速度为 $ 5a{t}_{0} $
C.汽车的最大速度为 $ 4a{t}_{0} $
D.汽车停止运动的时刻为 $ 14{t}_{0} $
答案:C
解析: $ 2{t}_{0} $ 时刻汽车的速度为 $ {v}_{1}=2a{t}_{0} $ , $ 3{t}_{0} $ 时刻汽车的速度为 $ {v}_{2}={v}_{1}-a{t}_{0}=a{t}_{0} $ ,则 $ 2{t}_{0} $ 至 $ 3{t}_{0} $ 时间内速度变化量 $ \mathrm{\Delta }v={v}_{2}-{v}_{1}=-a{t}_{0} $ ,故 $ \mathrm{A} $ 错误; $ 8{t}_{0} $ 时刻汽车的速度达到最大值, $ {v}_{\mathrm{m}}=2a{t}_{0}-a{t}_{0}+2a{t}_{0}-a{t}_{0}+2a{t}_{0}=4a{t}_{0} $ ,故 $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确;设汽车停止运动的时刻为 $ t $ ,由速度—时间公式有 $ 0={v}_{\mathrm{m}}-a(t-8{t}_{0}) $ ,结合 $ {v}_{\mathrm{m}}=4a{t}_{0} $ ,联立解得 $ t=12{t}_{0} $ ,故 $ \mathrm{D} $ 错误.
3.如图,滑雪轨道由光滑的倾斜直轨道 $ AB $ 和粗糙的水平轨道 $ BC $ 组成 $ {\rm .} t=0 $ 时运动员从 $ A $ 点由静止开始匀加速下滑,经过 $ B $ 点前后速度大小不变,之后在 $ BC $ 上做匀减速直线运动,最后停在 $ C $ 点.若第 $ 2\mathrm{s} $ 末和第 $ 6\mathrm{s} $ 末速度大小均为 $ 6\mathrm{m}/\mathrm{s} $ ,第 $ 4\mathrm{s} $ 末速度大小为 $ 10\mathrm{m}/\mathrm{s} $ .
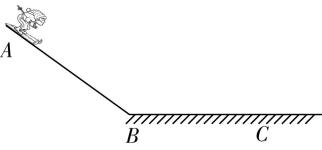
(1) 运动员何时恰好停在 $ C $ 点?
(2) 运动员何时恰好经过 $ B $ 点?
(3) 求运动员运动过程中的最大速度的大小.
答案:(1) $ 9\mathrm{s} $
(2) $ 3.6\mathrm{s} $
(3) $ 10.8\mathrm{m}/\mathrm{s} $
解析:(1) 运动员前 $ 2\mathrm{s} $ 内做匀加速运动,加速度大小 $ {a}_{1}=\dfrac{6}{2}\mathrm{m}/{\mathrm{s}}^{2}=3\mathrm{m}/{\mathrm{s}}^{2} $ ,若第 $ 4\mathrm{s} $ 末恰好经过 $ B $ 点,则 $ 4\mathrm{s} $ 末的速度 $ v={a}_{1}{t}_{4}=12\mathrm{m}/\mathrm{s} $ ,但是 $ 4\mathrm{s} $ 末的速度为 $ 10\mathrm{m}/\mathrm{s} $ ,可知 $ 4\mathrm{s} $ 末运动员已经做减速运动,减速运动的加速度 $ {a}_{2}=\dfrac{{v}_{6}-{v}_{4}}{{t}_{6}-{t}_{4}}=\dfrac{6-10}{6-4}\mathrm{m}/{\mathrm{s}}^{2}=-2\mathrm{m}/{\mathrm{s}}^{2} $ ,设运动员经过时间 $ t $ 到达 $ B $ 点,则 $ {v}_{B}={a}_{1}t={v}_{4}-{a}_{2}(4\mathrm{s}-t) $ , $ {v}_{6}={v}_{B}+{a}_{2}(6\mathrm{s}-t) $ ,解得 $ t=3.6\mathrm{s} $ , $ {v}_{B}=10.8\mathrm{m}/\mathrm{s} $ ,减速的时间为 $ t\prime =\dfrac{0-{v}_{B}}{{a}_{2}}=5.4\mathrm{s} $ ,则运动员恰好停在 $ C $ 点的时间 $ T=t+t\prime =9\mathrm{s} $ .
(2) 见(1)解析
(3) 见(1)解析
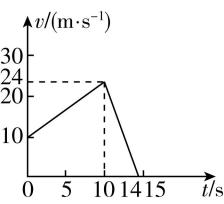
4.一辆汽车以 $ 36\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度在平直公路上匀速行驶.从某时刻起,汽车开始做匀加速运动,加速度大小为 $ 1.4\mathrm{m}/{\mathrm{s}}^{2} $ , $ 10\mathrm{s} $ 末因故突然紧急刹车,随后汽车逐渐停了下来.刹车时汽车做匀减速直线运动,加速度大小为 $ 6\mathrm{m}/{\mathrm{s}}^{2} $ .
(1) 求汽车 $ 10\mathrm{s} $ 末的速度大小;
(2) 求刹车后 $ 2\mathrm{s} $ 汽车的速度大小;
(3) 汽车刹车后经过多长时间停下来;
(4) 请你定量画出从该时刻起至汽车停止运动这段时间内汽车运动的速度—时间图像(图中应标注出关键点的时刻、速度的大小).
答案:(1) $ 24\mathrm{m}/\mathrm{s} $
(2) $ 12\mathrm{m}/\mathrm{s} $
(3) $ 4\mathrm{s} $
(4) 见解析
解析:(1) 规定汽车初速度方向为正方向,由题意知汽车匀加速运动阶段初速度 $ {v}_{0}=36\mathrm{k}\mathrm{m}/\mathrm{h}=10\mathrm{m}/\mathrm{s} $ ,加速度 $ {a}_{1}=1.4\mathrm{m}/{\mathrm{s}}^{2} $ ,则汽车 $ 10\mathrm{s} $ 末的速度 $ {v}_{1}={v}_{0}+{a}_{1}{t}_{1}=10\mathrm{m}/\mathrm{s}+1.4×10\mathrm{m}/\mathrm{s}=24\mathrm{m}/\mathrm{s} $ ,即汽车 $ 10\mathrm{s} $ 末的速度大小为 $ 24\mathrm{m}/\mathrm{s} $ .
(2) 刹车阶段汽车的加速度 $ {a}_{2}=-6\mathrm{m}/{\mathrm{s}}^{2} $ ,汽车减速到零所用时间 $ {t}_{3}=\dfrac{0-{v}_{1}}{{a}_{2}}=4\mathrm{s} $ ,故刹车 $ 2\mathrm{s} $ 后速度 $ {v}_{2}={v}_{1}+{a}_{2}{t}_{2}=24\mathrm{m}/\mathrm{s}+(-6)×2\mathrm{m}/\mathrm{s}=12\mathrm{m}/\mathrm{s} $ ,即刹车后 $ 2\mathrm{s} $ 汽车的速度大小为 $ 12\mathrm{m}/\mathrm{s} $ .
(3) 见(2)解析
(4) 由题意和前面分析可知, $ 0\sim 10\mathrm{s} $ 内汽车做匀加速直线运动, $ 10\sim 14\mathrm{s} $ 内汽车做匀减速直线运动,汽车运动的速度—时间图像如图所示.
 (多选)
(多选)




