课时1 匀变速直线运动的位移与时间的关系
一、刷基础
1.嫦娥三号登月探测器靠近月球后,先悬停在月面上方一定高度,之后关闭发动机,以 $ 1.6\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度竖直下落,经过 $ 2\mathrm{s} $ 到达月球表面,则嫦娥三号登月探测器悬停的高度为( )
A. $ 4\mathrm{m} $
B. $ 3.2\mathrm{m} $
C. $ 1.6\mathrm{m} $
D. $ 0.8\mathrm{m} $
答案:B
解析:根据位移—时间公式可得 $ x=\dfrac{1}{2}a{t}^{2}=3.2\mathrm{m} $ ,故 $ \mathrm{B} $ 正确.
2.某品牌无人驾驶汽车进行刹车性能测试,得到汽车在平直路面上紧急刹车(刹车加速度不变)过程中的位置坐标 $ x $ 随时间 $ t $ 变化的规律为 $ x=5+10t-2{t}^{2}(x $ 的单位是 $ \mathrm{m} $ , $ t $ 的单位是 $ \mathrm{s}) $ .则下列说法不正确的是( )
A.刹车后 $ 2\mathrm{s} $ 内的位移为 $ 17\mathrm{m} $
B.该汽车刹车的加速度为 $ -4\mathrm{m}/{\mathrm{s}}^{2} $
C.刹车后 $ 2\mathrm{s} $ 末的速度为 $ 2\mathrm{m}/\mathrm{s} $
D.该汽车刹车的初速度为 $ 10\mathrm{m}/\mathrm{s} $
答案:A
解析:已知汽车刹车过程中的位置坐标 $ x $ 随时间 $ t $ 变化的规律为 $ x=5+10t-2{t}^{2} $ ,结合匀变速直线运动位移—时间公式 $ x={v}_{0}t+\dfrac{1}{2}a{t}^{2} $ ,可得汽车刹车时的初速度和加速度分别为 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ 、 $ a=-4\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确;汽车从刹车到停下所用时间为 $ {t}_{0}=\dfrac{{v}_{0}}{-a}=2.5\mathrm{s} $ ,则刹车后 $ 2\mathrm{s} $ 末的速度为 $ {v}_{1}={v}_{0}+a{t}_{1}=(10-4×2)\mathrm{m}/\mathrm{s}=2\mathrm{m}/\mathrm{s} $ ,刹车后 $ 2\mathrm{s} $ 内的位移为 $ {x}_{1}={v}_{0}{t}_{1}+\dfrac{1}{2}a{t}_{1}^{2}=(10×2-\dfrac{1}{2}×4×{2}^{2})\mathrm{m}=12\mathrm{m} $ , $ \mathrm{A} $ 错误, $ \mathrm{C} $ 正确.本题选说法不正确的,故选 $ \mathrm{A} $ .
3.如图所示,机动车在斑马线前礼让行人是城市文明和交通规范的体现.司机小东驾驶汽车以 $ 43.2\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度,在平直的城市道路上沿直线行驶.他看到斑马线上有行人后立即以大小为 $ 2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度刹车,车停住时车头刚好碰到斑马线,等待行人 $ 10\mathrm{s} $ 后(人已走过),又用了 $ 8\mathrm{s} $ 时间匀加速至原来的速度.设开始刹车时为计时起点(即 $ t=0 $ ),求:

(1)汽车第 $ 4\mathrm{s} $ 末的速度大小;
(2)汽车在前 $ 10\mathrm{s} $ 内的位移大小;
(3)汽车因礼让行人而耽搁的时间.
答案:(1) $ 4\mathrm{m}/\mathrm{s} $ (2) $ 36\mathrm{m} $ (3) $ 17\mathrm{s} $
解析:(1)汽车的初速度大小为 $ {v}_{0}=43.2\mathrm{k}\mathrm{m}/\mathrm{h}=12\mathrm{m}/\mathrm{s} $ ,汽车的刹车时间为 $ {t}_{0}=\dfrac{{v}_{0}}{a}=6\mathrm{s} > 4\mathrm{s} $ ,所以汽车在第 $ 4\mathrm{s} $ 末时还未停下,速度大小为 $ {v}_{1}={v}_{0}-a{t}_{1}=4\mathrm{m}/\mathrm{s} $ .
(2)汽车在前 $ 6\mathrm{s} $ 减速停下,位移大小为 $ {x}_{1}={v}_{0}{t}_{0}-\dfrac{1}{2}a{t}_{0}^{2}=\dfrac{{v}_{0}}{2}{t}_{0}=36\mathrm{m} $ ,后 $ 4\mathrm{s} $ 静止,位移为零,故汽车在前 $ 10\mathrm{s} $ 内的位移大小等于刹车距离,为 $ 36\mathrm{m} $ .
(3)车匀加速运动的位移大小为 $ {x}_{2}=\dfrac{{v}_{0}{t}_{2}}{2}=48\mathrm{m} $ ,在没有行人时汽车匀速通过上述两段位移所用时间为 $ t\mathrm{\text{'}}=\dfrac{{x}_{1}+{x}_{2}}{{v}_{0}}=7\mathrm{s} $ ,由于礼让行人,汽车通过上述两段位移所用时间为 $ t={t}_{0}+{t}_{\text{等}}+{t}_{2}=24\mathrm{s} $ ,汽车因礼让行人而耽搁的时间为 $ \mathrm{\Delta }t=t-t\mathrm{\text{'}}=17\mathrm{s} $ .
4.在某两次升旗训练中,第一次国旗的运动可用 $ v-t $ 图中的虚线表示,第二次在开始阶段国旗的加速度稍大,但在国歌结束时国旗仍恰好到达最高点.下列选项中关于两次国旗运动的 $ v-t $ 图像,正确的是( )
A.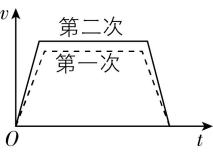
B.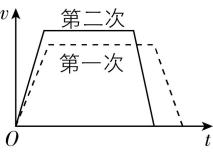
C.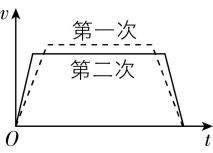
D.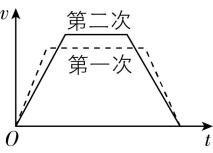
答案:C
解析: $ v-t $ 图像的斜率表示加速度,根据题意可知,第二次升旗在开始阶段国旗的加速度稍大,则第二次在开始阶段的 $ v-t $ 图像斜率较大,且两次都在国歌结束时国旗恰好到达最高点,则两次国旗的运动时间相同; $ v-t $ 图像与横轴围成的面积表示位移,由于两次国旗上升的高度相同,则两次 $ v-t $ 图像与横轴围成的面积相等, $ \mathrm{C} $ 正确.
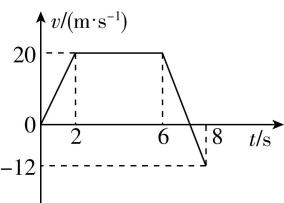
5.我国国产某品牌新能源汽车在平直的专用测试路段上做测试时的 $ v-t $ 图像如图所示,则( )
 (多选)
(多选)
A.汽车在 $ 1\mathrm{s} $ 时的加速度大于 $ 7\mathrm{s} $ 时的加速度
B.前 $ 6\mathrm{s} $ 内汽车的位移大小为 $ 100\mathrm{m} $
C. $ 8\mathrm{s} $ 时汽车离出发点最远
D. $ 7.25\mathrm{s} $ 时汽车的速度为0
答案:BD
解析: $ v-t $ 图像越陡表示加速度越大,由题图可知,汽车在 $ 1\mathrm{s} $ 时的加速度小于 $ 7\mathrm{s} $ 时的加速度, $ \mathrm{A} $ 错误; $ v-t $ 图像与时间轴所围的图形面积表示位移,由题图可知,前 $ 6\mathrm{s} $ 内汽车的位移大小为 $ x=\dfrac{4+6}{2}×20\mathrm{m}=100\mathrm{m} $ ,故 $ \mathrm{B} $ 正确;汽车 $ 8\mathrm{s} $ 内先向正方向运动,后向负方向运动, $ 8\mathrm{s} $ 时速度方向为负,所以 $ 8\mathrm{s} $ 前汽车速度已经反向, $ 8\mathrm{s} $ 时汽车离出发点不是最远, $ \mathrm{C} $ 错误;
$ 6\sim 8\mathrm{s} $ 时间内汽车的加速度为 $ a=\dfrac{-12-20}{8-6}\mathrm{m}/{\mathrm{s}}^{2}=-16\mathrm{m}/{\mathrm{s}}^{2} $ ,汽车 $ 6\mathrm{s} $ 时的速度为 $ 20\mathrm{m}/\mathrm{s} $ ,从该时刻起,汽车的速度减为零所需时间为 $ \mathrm{\Delta }t=\dfrac{0-{v}_{0}}{a}=\dfrac{0-20}{-16}\mathrm{s}=1.25\mathrm{s} $ ,即 $ 7.25\mathrm{s} $ 时汽车的速度为0,故 $ \mathrm{D} $ 正确.
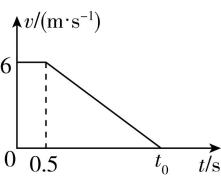
6.某小轿车驾驶员看到绿灯开始闪烁时,经短暂思考后开始刹车,小轿车在红灯刚亮时恰停在停止线上, $ v-t $ 图像如图所示.若绿灯开始闪烁时小轿车距停车线距离 $ L=10.5\mathrm{m} $ ,则( )
 (多选)
(多选)
A.小轿车刹车的加速度大小为 $ 2\mathrm{m}/{\mathrm{s}}^{2} $
B.小轿车的刹车距离为 $ 7.5\mathrm{m} $
C.绿灯开始闪烁到红灯刚亮的时间 $ {t}_{0}=3\mathrm{s} $
D.绿灯开始闪烁到红灯刚亮的时间 $ {t}_{0}=2.5\mathrm{s} $
答案:BC
解析:由题意可知小轿车在整个过程的位移大小 $ L=10.5\mathrm{m} $ ,小轿车匀速运动的位移大小 $ x={v}_{0}t=3\mathrm{m} $ ,所以小轿车的刹车距离 $ {x}_{1}=L-x=7.5\mathrm{m} $ ,故 $ \mathrm{B} $ 正确;刹车过程初速度为 $ 6\mathrm{m}/\mathrm{s} $ ,末速度为零,故平均速度为 $ 3\mathrm{m}/\mathrm{s} $ ,则有 $ \overline{v}{t}_{1}=7.5\mathrm{m} $ ,可得刹车时间为 $ {t}_{1}=2.5\mathrm{s} $ ,绿灯开始闪烁到红灯刚亮的时间为 $ {t}_{0}={t}_{1}+t=3\mathrm{s} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误;刹车的加速度大小为 $ a=\dfrac{\mathrm{\Delta }v}{{t}_{1}}=\dfrac{6\mathrm{m}/\mathrm{s}}{2.5\mathrm{s}}=2.4\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{A} $ 错误.
7.某同学乘电梯上楼,电梯先向上加速,后匀速,最后减速到速度为零,在此过程中,电梯的位移随时间变化的规律可能是( )
A.
B.
C.
D.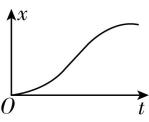
答案:D
解析:因为 $ x-t $ 图像切线的斜率表示速度,可知当电梯先向上加速,后匀速,最后减速到速度为零的过程中,图像切线的斜率先增大,后不变,最后减小直到斜率减到零,故 $ \mathrm{D} $ 正确.
8.如图所示为甲、乙两辆汽车从 $ t=0 $ 时刻开始做直线运动的位置—时间图像,甲的图像为抛物线,且坐标原点即为抛物线最低点,乙的图像为倾斜直线.已知甲图线在 $ t=\dfrac{{t}_{0}}{4} $ 时刻的切线与乙图线平行,图中坐标均为已知量.则在 $ t=0 $ 时刻甲、乙两车间的距离为( )

A. $ \dfrac{3}{2}{x}_{0} $
B. $ {x}_{0} $
C. $ \dfrac{5}{2}{x}_{0} $
D. $ 2{x}_{0} $
答案:A
解析:由匀变速直线运动的位移—时间公式 $ x={v}_{0}t+\dfrac{1}{2}a{t}^{2} $ 可知,甲做匀变速直线运动,且 $ {v}_{0}=0 $ ,代入题图中数据可得 $ a=\dfrac{6{x}_{0}}{{t}_{0}^{2}} $ ,设 $ t=0 $ 时刻乙位置坐标为 $ x $ ,则乙的速度为 $ {v}_{乙}=\dfrac{3{x}_{0}-x}{{t}_{0}} $ ,由速度—时间公式可得甲在 $ t=\dfrac{{t}_{0}}{4} $ 时刻的速度为 $ {v}_{甲}=a\dfrac{{t}_{0}}{4} $ ,由题意知 $ t=\dfrac{{t}_{0}}{4} $ 时刻 $ {v}_{甲}={v}_{乙} $ ,联立解得 $ x=\dfrac{3}{2}{x}_{0} $ ,故 $ t=0 $ 时刻甲、乙两车间的距离为 $ \dfrac{3{x}_{0}}{2} $ .故 $ \mathrm{A} $ 正确.
9.将一物块置于光滑水平面上,现给物块施加一水平向右的力,物块以加速度 $ {a}_{1} $ 做匀加速直线运动,经过一段时间,立即改为水平向左的力,物块以加速度 $ {a}_{2} $ 运动,经过相等时间物块回到了原位置,则两次加速度大小之比为( )

A. $ 1:1 $
B. $ 1:2 $
C. $ 1:3 $
D. $ 1:4 $
答案:C
解析:根据题意,设加速阶段时间为 $ t $ ,由运动学公式有 $ x=\dfrac{1}{2}{a}_{1}{t}^{2} $ , $ {v}_{1}={a}_{1}t $ ,又有 $ -x={v}_{1}t-\dfrac{1}{2}{a}_{2}{t}^{2} $ ,联立解得 $ {a}_{1}:{a}_{2}=1:3 $ ,故 $ \mathrm{C} $ 正确.
10.物体从 $ A $ 点由静止出发,先以加速度大小 $ {a}_{1} $ 做匀加速直线运动加速到 $ v $ 后,立即以大小为 $ {a}_{2} $ 的加速度做匀减速直线运动至 $ B $ 点速度恰好减为零,所用总时间为 $ t $ .若物体以速度 $ {v}_{0} $ 匀速通过 $ AB $ ,所用时间也为 $ t $ ,则( )(多选)
A. $ v=2{v}_{0} $
B. $ \dfrac{1}{{a}_{1}}+\dfrac{1}{{a}_{2}}=\dfrac{t}{v} $
C. $ \dfrac{1}{{a}_{1}}-\dfrac{1}{{a}_{2}}=\dfrac{t}{2v} $
D. $ \dfrac{1}{{a}_{1}}+\dfrac{1}{{a}_{2}}=\dfrac{t}{2v} $
答案:AB
解析:由运动学公式有 $ x={v}_{0}t=\dfrac{v}{2}{t}_{1}+\dfrac{v}{2}{t}_{2}=\dfrac{v}{2}({t}_{1}+{t}_{2})=\dfrac{v}{2}t $ ,解得 $ v=2{v}_{0} $ , $ \mathrm{A} $ 正确;由 $ {t}_{1}=\dfrac{v}{{a}_{1}} $ 、 $ {t}_{2}=\dfrac{v}{{a}_{2}} $ 得 $ t=\dfrac{v}{{a}_{1}}+\dfrac{v}{{a}_{2}} $ ,即 $ \dfrac{t}{v}=\dfrac{1}{{a}_{1}}+\dfrac{1}{{a}_{2}} $ , $ \mathrm{B} $ 正确, $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
11.航母阻拦索可将高速运动的舰载机拦停.若我国一架歼 $ -15 $ 舰载机在静止的辽宁舰上着舰,在阻拦索的作用下做匀减速直线运动,速度从 $ v $ 减为0所用的时间为 $ t $ ,则该舰载机与阻拦索作用过程中通过的距离为( )
A. $ vt $
B. $ 2vt $
C. $ \dfrac{vt}{2} $
D. $ \dfrac{3vt}{2} $
答案:C
解析:根据匀变速直线运动的规律可知,该舰载机与阻拦索作用过程中通过的距离 $ x=\dfrac{0+v}{2}t=\dfrac{vt}{2} $ ,故 $ \mathrm{C} $ 正确.
12.如图所示,一辆赛车在平直赛道上做匀加速直线运动,途经 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 四个标志杆,其中 $ {x}_{AB}=6\mathrm{m} $ , $ {x}_{CD}=9\mathrm{m} $ .赛车手发现自己通过 $ AB $ 和 $ CD $ 这两段位移的时间均为 $ 1\mathrm{s} $ ,而通过 $ BC $ 段时间仅为 $ 0.5\mathrm{s} $ ,若将赛车看成质点,则以下说法中正确的是( )
 (多选)
(多选)
A.赛车做匀加速直线运动的加速度 $ a=1.5\mathrm{m}/{\mathrm{s}}^{2} $
B.赛车做匀加速直线运动的加速度 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $
C.赛道上 $ B $ 、 $ C $ 间的距离为 $ 7.5\mathrm{m} $
D.利用以上数据可以计算出赛车经过 $ A $ 点时的速度 $ {v}_{A}=5\mathrm{m}/\mathrm{s} $
答案:BD
解析:如图,设赛车通过 $ AB $ 的中间时刻对应位置为 $ P $ ,通过 $ CD $ 的中间时刻对应位置为 $ Q $ ,则根据匀变速直线运动中间时刻的瞬时速度等于平均速度,有 $ {v}_{P}=\dfrac{{x}_{AB}}{{t}_{1}}=6\mathrm{m}/\mathrm{s} $ , $ {v}_{Q}=\dfrac{{x}_{CD}}{{t}_{1}}=9\mathrm{m}/\mathrm{s} $ ,赛车从 $ P $ 到 $ Q $ 的运动时间为 $ t=\dfrac{1}{2}\mathrm{s}+\dfrac{1}{2}\mathrm{s}+0.5\mathrm{s}=1.5\mathrm{s} $ ,则加速度 $ a=\dfrac{{v}_{Q}-{v}_{P}}{t}=2\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;根据速度—时间公式可得赛车经过 $ B $ 点的瞬时速度为 $ {v}_{B}={v}_{P}+a\dfrac{{t}_{1}}{2}=7\mathrm{m}/\mathrm{s} $ ,由 $ B $ 到 $ C $ 做匀加速直线运动,故 $ B $ 、 $ C $ 间的距离为 $ x={v}_{B}{t}_{2}+\dfrac{1}{2}a{t}_{2}^{2}=3.75\mathrm{m} $ , $ \mathrm{C} $ 错误;赛车经过 $ A $ 点时的速度为 $ {v}_{A}={v}_{P}-a\dfrac{{t}_{1}}{2}=5\mathrm{m}/\mathrm{s} $ , $ \mathrm{D} $ 正确.

13.一汽车在平直公路上以 $ 72\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度行驶,突然发现前方道路出现状况,驾驶员立即刹车,汽车做匀减速直线运动,刹车后 $ 2\mathrm{s} $ 内的位移大小为 $ 30\mathrm{m} $ .求:
(1) 汽车刹车后 $ 2\mathrm{s} $ 末的速度大小;
(2) 汽车刹车后 $ 5\mathrm{s} $ 内的位移大小.
答案:(1) $ 10\mathrm{m}/\mathrm{s} $
(2) $ 40\mathrm{m} $
解析:(1) 汽车的初速度为 $ {v}_{0}=72\mathrm{k}\mathrm{m}/\mathrm{h}=20\mathrm{m}/\mathrm{s} $ ,假设 $ 2\mathrm{s} $ 时汽车恰好停下,则 $ 2\mathrm{s} $ 内汽车的位移 $ {x}_{0}=\dfrac{{v}_{0}}{2}{t}_{1}=20\mathrm{m} $ ,由于 $ {x}_{0} < 30\mathrm{m} $ ,则汽车在 $ 2\mathrm{s} $ 时并未停下.设汽车刹车的加速度为 $ a $ ,刹车后 $ 2\mathrm{s} $ 内,由运动学公式有 $ x={v}_{0}{t}_{1}+\dfrac{1}{2}a{t}_{1}^{2} $ ,解得 $ a=-5\mathrm{m}/{\mathrm{s}}^{2} $ ,由运动学公式有 $ v={v}_{0}+a{t}_{1} $ ,则汽车 $ 2\mathrm{s} $ 末的速度大小为 $ v=10\mathrm{m}/\mathrm{s} $ .
(2) 设汽车经过时间 $ t $ 停止运动,则有 $ 0={v}_{0}+at $ ,得 $ t=4\mathrm{s} $ ,故 $ 5\mathrm{s} $ 时汽车已停止运动,汽车刹车后 $ 5\mathrm{s} $ 内的位移与汽车在 $ 4\mathrm{s} $ 内的位移相等,设汽车 $ 4\mathrm{s} $ 内的位移为 $ x\prime $ , $ x\prime ={v}_{0}t+\dfrac{1}{2}a{t}^{2}=40\mathrm{m} $ ,所以汽车刹车后 $ 5\mathrm{s} $ 内位移大小为 $ 40\mathrm{m} $ .
二、刷提升
1.一小车从 $ A $ 地由静止开始做匀加速直线运动驶向 $ B $ 地,已知小车在最初的 $ t $ 时间内运动的位移为 $ s $ ,在到达 $ B $ 地前最后的 $ t $ 时间内,小车运动的位移为 $ ks(k $ 为常数,且 $ k > 1) $ ,则小车从 $ A $ 地到 $ B $ 地的时间为( )
A. $ \dfrac{(k+1)t}{2} $
B. $ \dfrac{(k-1)t}{2} $
C. $ \dfrac{(k+2)t}{2} $
D. $ \dfrac{{\left(k+1\right) ^ {2}}t}{2} $
答案:A
解析:根据题意,由匀变速直线运动位移—时间公式可得,在最初的 $ t $ 时间内 $ s=\dfrac{1}{2}a{t}^{2} $ ,设小车运动的总时间为 $ T $ ,在最后的 $ t $ 时间内 $ ks=\dfrac{1}{2}a{T}^{2}-\dfrac{1}{2}a(T-t)^{2} $ ,联立解得 $ T=\dfrac{k+1}{2}t $ ,故 $ \mathrm{A} $ 正确.
2.一旅客在火车站某站台7号车厢候车线处候车,他发现动车进站时第5节车厢经过他用了 $ 0.83\mathrm{s} $ ,动车停下时他刚好在第7节车厢门口,车门靠近动车前进方向一端.每节车厢的长度相同,不计各节车厢连接处的长度,若动车进站时做匀减速直线运动,则第6节车厢经过他的时间约为( )
A. $ 2\mathrm{s} $
B. $ 1\mathrm{s} $
C. $ 0.64\mathrm{s} $
D. $ 0.5\mathrm{s} $
答案:A
解析:设每节车厢的长度为 $ L $ ,动车做匀减速直线运动,末速度为零,则由逆向思维将动车减速进站的过程反向看作初速度为零的匀加速直线运动,则第5、6节车厢经过他时,有 $ 2L=\dfrac{1}{2}a{t}_{2}^{2} $ ,第6节车厢经过他时,有 $ L=\dfrac{1}{2}a{t}_{1}^{2} $ ,第5节车厢经过他的时间 $ t={t}_{2}-{t}_{1}=0.83\mathrm{s} $ ,联立解得第6节车厢经过他的时间约为 $ {t}_{1}=2\mathrm{s} $ ,故 $ \mathrm{A} $ 正确.
3.某小物块在一长木板上运动时,两者运动的 $ v-t $ 图像如图所示,已知小物块始终在长木板上,且 $ 1.5\sim 4\mathrm{s} $ 内二者的 $ v-t $ 图线重合.则( )
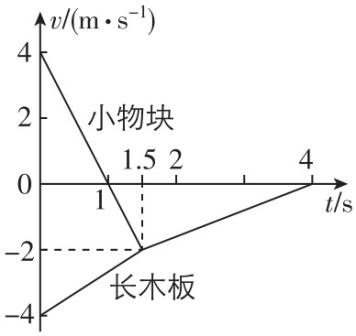
A.整个过程小物块相对于长木板向负方向运动
B.小物块相对于长木板运动的位移大小为 $ 6\mathrm{m} $
C.长木板在 $ 0\sim 4\mathrm{s} $ 内的平均速度大小是 $ 2\mathrm{m}/\mathrm{s} $
D.在 $ 0\sim 4\mathrm{s} $ 内长木板和小物块的平均加速度相同
答案:B
解析:由 $ v-t $ 图像可知, $ 0\sim 1.5\mathrm{s} $ 内小物块相对于长木板向正方向运动, $ 1.5\sim 4\mathrm{s} $ 内小物块与长木板相对静止, $ \mathrm{A} $ 错误;在 $ 0\sim 1.5\mathrm{s} $ 内,两图线与纵轴所围图形的面积等于小物块相对于长木板运动的位移大小,为 $ \mathrm{\Delta }x=\dfrac{(4+4)×1.5}{2}\mathrm{m}=6\mathrm{m} $ , $ \mathrm{B} $ 正确;在 $ v-t $ 图像中,图线与时间轴围成图形的面积表示位移,因此在 $ 0\sim 1.5\mathrm{s} $ 内长木板的位移大小 $ {x}_{1}=\dfrac{(2+4)×1.5}{2}\mathrm{m}=4.5\mathrm{m} $ ,在 $ 1.5\sim 4\mathrm{s} $ 内长木板的位移大小 $ {x}_{2}=\dfrac{2×(4-1.5)}{2}\mathrm{m}=2.5\mathrm{m} $ ,因此长木板在 $ 0\sim 4\mathrm{s} $ 内的平均速度大小 $ \overline{v}=\dfrac{{x}_{1}+{x}_{2}}{{t}_{4}}=\dfrac{4.5+2.5}{4}\mathrm{m}/\mathrm{s}=1.75\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 错误;在 $ 0\sim 4\mathrm{s} $ 内长木板和小物块的速度变化量大小相等、方向相反,故两者的平均加速度大小相等、方向相反, $ \mathrm{D} $ 错误.
4.风洞被称为飞行器的摇篮,我国的风洞技术世界领先.在某次实验中将一小白鼠静止放于风洞左侧入口处,小白鼠立刻开始以大小为 $ {a}_{1}=1\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度在风洞中做匀加速直线运动,小白鼠加速运动时所能达到的最大速度为 $ {v}_{\mathrm{m}}=6\mathrm{m}/\mathrm{s} $ ,达到最大速度后将以最大速度做匀速直线运动,当小白鼠运动 $ {t}_{1}=5\mathrm{s} $ 时突然打开风洞开关,小白鼠受到大小、方向均不变的风的持续作用,开始做匀减速直线运动,匀减速运动的加速度大小为 $ {a}_{2}=0.5\mathrm{m}/{\mathrm{s}}^{2} $ ,风洞作用时间为 $ {t}_{2}=14\mathrm{s} $ ,风洞开关关闭后小白鼠继续以恒定的加速度大小 $ {a}_{1}=1\mathrm{m}/{\mathrm{s}}^{2} $ 在风洞中向风洞右侧出口处运动,又经过时间 $ {t}_{3}=10\mathrm{s} $ ,小白鼠恰好运动到风洞右侧出口.求:
(1) 风洞开关关闭时小白鼠运动的速度大小;
(2) 风洞的长度.
答案:(1) $ 2\mathrm{m}/\mathrm{s} $
(2) $ 61.5\mathrm{m} $
解析:(1) 根据题意可知,小白鼠先以 $ {a}_{1}=1\mathrm{m}/{\mathrm{s}}^{2} $ 做匀加速直线运动,当 $ {t}_{1}=5\mathrm{s} $ 时,设小白鼠速度为 $ {v}_{0} $ ,则 $ {v}_{0}={a}_{1}{t}_{1} $ ,
解得 $ {v}_{0}=5\mathrm{m}/\mathrm{s} $ ,
突然打开风洞开关,小白鼠又以 $ {a}_{2}=0.5\mathrm{m}/{\mathrm{s}}^{2} $ 做匀减速直线运动,风洞作用时间为 $ {t}_{2} $ ,则风洞开关关闭时有 $ v={v}_{0}-{a}_{2}{t}_{2} $ ,
解得此时速度 $ v=-2\mathrm{m}/\mathrm{s} $ ,
故风洞开关关闭时小白鼠运动的速度大小为 $ 2\mathrm{m}/\mathrm{s} $ .
(2) 由题知,小白鼠先以 $ {a}_{1}=1\mathrm{m}/{\mathrm{s}}^{2} $ 做匀加速直线运动,其位移大小 $ {x}_{1}=\dfrac{1}{2}{a}_{1}{t}_{1}^{2}=12.5\mathrm{m} $ ,打开风洞开关,又以 $ {a}_{2}=0.5\mathrm{m}/{\mathrm{s}}^{2} $ 做匀减速直线运动,其位移大小 $ {x}_{2}={v}_{0}{t}_{2}-\dfrac{1}{2}{a}_{2}{t}_{2}^{2} $ ,解得 $ {x}_{2}=21\mathrm{m} $ ,
风洞开关关闭后小白鼠继续以恒定的加速度 $ {a}_{1}=1\mathrm{m}/{\mathrm{s}}^{2} $ 先向左做匀减速直线运动,后向右做匀加速直线运动,因为最大速度为 $ {v}_{\mathrm{m}} $ ,设经过 $ \mathrm{\Delta }t $ 达到最大速度,则 $ {v}_{\mathrm{m}}=v+{a}_{1}\mathrm{\Delta }t $ ,可得 $ \mathrm{\Delta }t=8\mathrm{s} $ ,
经过时间 $ {t}_{3}=10\mathrm{s} $ ,小白鼠恰好运动到风洞右侧出口,这段时间内其位移大小 $ {x}_{3}=\dfrac{v+{v}_{\mathrm{m}}}{2}\mathrm{\Delta }t+{v}_{\mathrm{m}}({t}_{3}-\mathrm{\Delta }t) $ ,
解得 $ {x}_{3}=28\mathrm{m} $ ,
所以风洞的长度 $ L={x}_{1}+{x}_{2}+{x}_{3}=61.5\mathrm{m} $ .
5.四旋翼无人机在地面上从 $ t=0 $ 时刻由静止开始竖直起飞.经历匀加速、匀速及匀减速三个运动过程, $ t=25\mathrm{s} $ 后悬停在距离地面某一高度处.其位移 $ x $ 随时间 $ t $ 变化的关系图像如图所示,其中 $ ab $ 段为倾斜直线,其余部分为曲线.求:
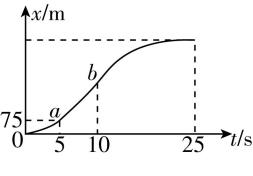
(1) 匀速运动的位移大小;
(2) 匀加速和匀减速阶段的加速度大小之比;
(3) 悬停处距离地面的高度.
答案:(1) $ 150\mathrm{m} $
(2) $ 3:1 $
(3) $ 450\mathrm{m} $
解析:(1) 设无人机匀加速运动阶段的加速度大小为 $ {a}_{1} $ ,位移大小为 $ {x}_{1} $ ,时间为 $ {t}_{1} $ ,匀速运动阶段的速度大小为 $ v $ ,位移大小为 $ {x}_{2} $ ,在 $ 0\sim 5\mathrm{s} $ 内,根据位移—时间公式有 $ {x}_{1}=\dfrac{1}{2}{a}_{1}{t}_{1}^{2} $ ,由题图知 $ 75\mathrm{m}=\dfrac{1}{2}×{a}_{1}×{5}^{2}(\mathrm{m}) $ ,解得 $ {a}_{1}=6\mathrm{m}/{\mathrm{s}}^{2} $ ,匀速运动阶段的速度大小 $ v={a}_{1}{t}_{1} $ ,代入数据得 $ v=30\mathrm{m}/\mathrm{s} $ ,匀速运动阶段运动的时间为 $ {t}_{2}=(10-5)\mathrm{s}=5\mathrm{s} $ ,匀速运动阶段位移大小 $ {x}_{2}=v{t}_{2} $ ,代入数据解得 $ {x}_{2}=150\mathrm{m} $ .
(2) 在 $ 10\sim 25\mathrm{s} $ 内,无人机做匀减速运动,设加速度大小为 $ {a}_{2} $ ,由题图知,在匀减速阶段有 $ 0-v=-{a}_{2}{t}_{3} $ ,得 $ {a}_{2}=\dfrac{30-0}{15}\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,所以 $ \dfrac{{a}_{1}}{{a}_{2}}=\dfrac{3}{1} $ .
(3) 在 $ 10\sim 25\mathrm{s} $ 内,有 $ {x}_{3}=\dfrac{1}{2}(v+0){t}_{3}=225\mathrm{m} $ ,则无人机悬停处距离地面的高度 $ ℎ={x}_{1}+{x}_{2}+{x}_{3}=75\mathrm{m}+150\mathrm{m}+225\mathrm{m}=450\mathrm{m} $ .





 (多选)
(多选) (多选)
(多选)





 (多选)
(多选)

