课时2 匀变速直线运动的速度与位移的关系
一、刷基础
1.汽车在关闭发动机后可视为做匀减速直线运动,前进 $ 60\mathrm{m} $ 的过程中,速度由 $ 7\mathrm{m}/\mathrm{s} $ 减小到 $ 5\mathrm{m}/\mathrm{s} $ ,若再经过 $ 10\mathrm{s} $ ,则汽车又将前进( )
A. $ 60\mathrm{m} $
B. $ 40\mathrm{m} $
C. $ 70\mathrm{m} $
D. $ 80\mathrm{m} $
答案:B
解析:根据匀变速直线运动速度—位移公式有 $ {v}^{2}-{v}_{0}^{2}=-2ax $ ,可得汽车减速过程的加速度大小为 $ a=0.2\mathrm{m}/{\mathrm{s}}^{2} $ ,则汽车从 $ 5\mathrm{m}/\mathrm{s} $ 减速到0所用时间为 $ {t}_{0}=\dfrac{5}{0.2}\mathrm{s}=25\mathrm{s} > 10\mathrm{s} $ ,则再运动 $ 10\mathrm{s} $ ,汽车又将前进的距离为 $ {x}_{1}=vt-\dfrac{1}{2}a{t}^{2}=40\mathrm{m} $ ,故 $ \mathrm{B} $ 正确.
2.已知“歼 $ -15 $ ”在跑道上做匀加速直线运动时产生的最大加速度为 $ 5.0\mathrm{m}/{\mathrm{s}}^{2} $ ,起飞的最小速度为 $ 50\mathrm{m}/\mathrm{s} $ ,弹射系统能够使“歼 $ -15 $ ”获得的最大初速度为 $ 25\mathrm{m}/\mathrm{s} $ ,设航母处于静止状态.
(1) “歼 $ -15 $ ”在跑道上至少加速多长时间才能起飞?
(2) “歼 $ -15 $ ”在跑道上至少加速多长距离才能起飞?
(3) 若航母上不装弹射系统,设航母跑道长 $ L=160\mathrm{m} $ ,“歼 $ -15 $ ”仍能从航母上正常起飞,则航母航行速度至少为多少?
答案:(1) $ 5\mathrm{s} $
(2) $ 187.5\mathrm{m} $
(3) $ 10\mathrm{m}/\mathrm{s} $
解析:(1) 根据匀变速直线运动的速度—时间公式 $ v={v}_{0}+at $ ,得 $ t=\dfrac{v-{v}_{0}}{a}=5\mathrm{s} $ .
(2) 根据速度—位移公式 $ {v}^{2}-{v}_{0}^{2}=2ax $ ,得“歼 $ -15 $ ”在跑道上加速的最小距离 $ x=\dfrac{{v}^{2}-{v}_{0}^{2}}{2a}=187.5\mathrm{m} $ .
(3) 解法一:为保证“歼 $ -15 $ ”能安全起飞,航空母舰的航行方向即为“歼 $ -15 $ ”起飞时的方向,而它的速度即为“歼 $ -15 $ ”的初速度,以航空母舰为参考系,有 $ (v-v{\prime }_{0})^{2}=2aL $ ,解得 $ v{\prime }_{0}=10\mathrm{m}/\mathrm{s} $ ,航空母舰应至少以 $ 10\mathrm{m}/\mathrm{s} $ 的速度沿“歼 $ -15 $ ”起飞方向航行.
解法二:以地面为参考系,设“歼 $ -15 $ ”在航空母舰上运动的时间为 $ {t}_{1} $ ,则在 $ {t}_{1} $ 时间内航空母舰做匀速运动的位移大小为 $ {x}_{1}=v{\prime }_{0}{t}_{1} $ ,“歼 $ -15 $ ”通过的位移大小为 $ {x}_{2}=v{\prime }_{0}{t}_{1}+\dfrac{1}{2}a{t}_{1}^{2} $ ,“歼 $ -15 $ ”起飞时 $ v=v{\prime }_{0}+a{t}_{1} $ ,由题意可知 $ {x}_{2}-{x}_{1}=L $ ,联立解得 $ v{\prime }_{0}=10\mathrm{m}/\mathrm{s} $ ,航空母舰应至少以 $ 10\mathrm{m}/\mathrm{s} $ 的速度沿“歼 $ -15 $ ”起飞方向航行.
3.一观察者站在列车第一节车厢前端,当列车从静止开始做匀加速直线运动时( )
A.每节车厢末端经过观察者的速度之比是 $ 1:2:3:\cdots :n $
B.每节车厢经过观察者所用的时间之比是 $ 1:3:5:\cdots :(2n-1) $
C.在连续相等时间里经过观察者的车厢数之比是 $ 1:4:9:\cdots :{n}^{2} $
D.在连续相等时间里经过观察者的车厢数之比是 $ 1:3:5:\cdots :(2n-1) $
答案:D
解析:列车从静止开始做匀加速直线运动,根据 $ {v}^{2}=2ax $ ,可知 $ v=\sqrt{2ax} $ ,所以每节车厢末端经过观察者的速度之比是 $ 1:\sqrt{2}:\sqrt{3}:\cdots :\sqrt{n} $ , $ \mathrm{A} $ 错误;根据 $ t=\dfrac{v}{a} $ ,可知每节车厢末端经过观察者的时刻之比是 $ 1:\sqrt{2}:\sqrt{3}:\cdots :\sqrt{n} $ ,则每节车厢经过观察者所用的时间之比是 $ 1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):\cdots :(\sqrt{n}-\sqrt{n-1}) $ , $ \mathrm{B} $ 错误;根据初速度为0的匀加速直线运动在连续相等时间内的位移之比 $ {x}_{1}:{x}_{2}:{x}_{3}:\cdots :{x}_{n}=1:3:5:\cdots :(2n-1) $ ,可知在连续相等时间里经过观察者的车厢数之比是 $ 1:3:5:\cdots :(2n-1) $ , $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
4.港珠澳大桥是中国境内一座连接香港、广东珠海和澳门的桥隧工程.图为港珠澳大桥上四段长度为 $ 110\mathrm{m} $ 的等跨钢箱连续梁桥,若汽车(可视为质点)从 $ a $ 点由静止开始做匀加速直线运动,通过 $ ab $ 段的时间为 $ t $ .则( )
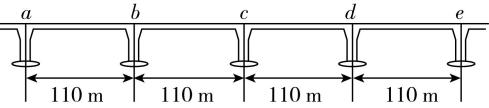
A.通过 $ bc $ 段的时间为 $ \sqrt{2}t $
B.通过 $ ac $ 段的平均速度等于通过 $ b $ 点的瞬时速度
C.通过 $ b $ 、 $ c $ 、 $ d $ 、 $ e $ 点的瞬时速度之比 $ {v}_{b}:{v}_{c}:{v}_{d}:{v}_{e}=1:2:3:4 $
D.通过 $ bc $ 段和 $ de $ 段所用时间之比为 $ (\sqrt{2}-1):(2-\sqrt{3}) $
答案:D
解析:由初速度为零的匀加速直线运动中通过连续相等的位移所用时间之比可知,汽车经过 $ ab $ 、 $ bc $ 、 $ cd $ 、 $ de $ 段所用时间之比为 $ {t}_{1}:{t}_{2}:{t}_{3}:{t}_{4}=1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):(2-\sqrt{3}) $ ,因为通过 $ ab $ 段的时间为 $ t $ ,故通过 $ bc $ 段的时间为 $ (\sqrt{2}-1)t $ ,通过 $ bc $ 段和 $ de $ 段所用时间之比为 $ (\sqrt{2}-1):(2-\sqrt{3}) $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{D} $ 正确; $ b $ 点对应 $ ae $ 段的中间时刻,所以通过 $ ae $ 段的平均速度等于通过 $ b $ 点的瞬时速度,故 $ \mathrm{B} $ 错误;根据 $ v=\sqrt{2ax} $ 可得通过的位移为 $ x $ 、 $ 2x $ 、 $ 3x $ 、 $ 4x $ 的瞬时速度之比 $ {v}_{b}:{v}_{c}:{v}_{d}:{v}_{e}=1:\sqrt{2}:\sqrt{3}:2 $ ,故 $ \mathrm{C} $ 错误.
5.如图甲所示,一猎豹(可视为质点)捕猎时从静止开始在平直的草原上做匀加速直线运动,将其开始运动的时刻记为 $ t=0 $ ,其速度的平方 $ {v}^{2} $ 随位移 $ x $ 变化的关系可用如图乙所示的 $ {v}^{2}-x $ 图像表示,关于猎豹的运动,下列说法正确的是( )
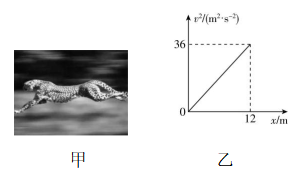
A.猎豹做匀加速直线运动的加速度大小为 $ 1.5\mathrm{m}/{\mathrm{s}}^{2} $
B.猎豹在 $ t=6\mathrm{s} $ 时的速度大小为 $ 18\mathrm{m}/\mathrm{s} $
C.猎豹在 $ 0\sim 12\mathrm{m} $ 内的平均速度大小为 $ 3\mathrm{m}/\mathrm{s} $
D.猎豹从 $ 0\sim 12\mathrm{m} $ 所用的时间为 $ 8\mathrm{s} $
答案:AC
解析:根据速度—位移关系有 $ {v}^{2}-{v}_{0}^{2}=2ax $ ,整理得 $ {v}^{2}={v}_{0}^{2}+2ax $ ,则可知图像的斜率为 $ k=2a=\dfrac{36}{12}\mathrm{m}/{\mathrm{s}}^{2}=3\mathrm{m}/{\mathrm{s}}^{2} $ ,则 $ a=1.5\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{A} $ 正确; $ t=6\mathrm{s} $ 时的速度大小为 $ {v}_{2}=at=9\mathrm{m}/\mathrm{s} $ , $ \mathrm{B} $ 错误;根据图像可知,在位移为 $ 12\mathrm{m} $ 时,速度为 $ {v}_{1}=6\mathrm{m}/\mathrm{s} $ ,则 $ 0\sim 12\mathrm{m} $ 内的平均速度大小为 $ \overline{v}=\dfrac{0+6}{2}\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确;从 $ 0\sim 12\mathrm{m} $ 所用的时间为 $ t=\dfrac{{v}_{1}}{a}=4\mathrm{s} $ , $ \mathrm{D} $ 错误.
二、刷提升
1.一个做匀加速直线运动的物体从 $ A $ 点运动到 $ B $ 点, $ A $ 、 $ B $ 两点间的距离为 $ x $ .它通过 $ A $ 、 $ B $ 两点时的速度分别为 $ {v}_{1} $ 和 $ {v}_{2} $ ,则运动至离 $ A $ 点 $ \dfrac{x}{3} $ 处的速度 $ {v}_{3} $ 为( )
A. $ \dfrac{{v}_{2}-2{v}_{1}}{3} $
B. $ \dfrac{{v}_{2}+2{v}_{1}}{3} $
C. $ \sqrt{\dfrac{{v}_{2}^{2}-2{v}_{1}^{2}}{3}} $
D. $ \sqrt{\dfrac{{v}_{2}^{2}+2{v}_{1}^{2}}{3}} $
答案:D
解析:根据匀变速直线运动的速度与位移的关系,有 $ {v}_{2}^{2}-{v}_{1}^{2}=2ax $ , $ {v}_{3}^{2}-{v}_{1}^{2}=2a\cdot \dfrac{x}{3} $ ,两式作比,可得 $ {v}_{3}=\sqrt{\dfrac{{v}_{2}^{2}+2{v}_{1}^{2}}{3}} $ ,故选 $ \mathrm{D} $ .
2.如图所示,小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,图中1、2、3、4、5为小球运动过程中连续五次曝光的位置.若连续两次曝光的时间间隔均为 $ T $ ,每块砖的厚度均为 $ d $ ,则下列说法正确的是( )
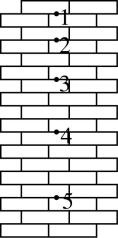
A.小球通过位置2时的速度大小为 $ \dfrac{3d}{2T} $
B.小球通过位置4时的速度大小为 $ \dfrac{7d}{2T} $
C.小球下落的加速度大小为 $ \dfrac{d}{{T}^{2}} $
D.位置1是小球释放的初始位置
答案:C
解析:小球通过位置2时的速度等于其从位置1运动到位置3过程中的平均速度,即 $ {v}_{2}=\dfrac{{x}_{13}}{2T}=\dfrac{5d}{2T} $ ,同理可得小球通过位置4时的速度大小 $ {v}_{4}=\dfrac{{x}_{35}}{2T}=\dfrac{9d}{2T} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;小球下落的加速度大小 $ a=\dfrac{\mathrm{\Delta }x}{{T}^{2}}=\dfrac{d}{{T}^{2}} $ ,故 $ \mathrm{C} $ 正确;小球通过位置1时的速度大小 $ {v}_{1}={v}_{4}-a\cdot 3T=\dfrac{3d}{2T}\ne 0 $ ,所以位置1并非小球释放的初始位置,故 $ \mathrm{D} $ 错误.
3.物体做变加速直线运动,依次经过 $ A $ 、 $ B $ 、 $ C $ 三点, $ B $ 为 $ AC $ 段的中点,物体在 $ AB $ 段的加速度恒为 $ {a}_{1} $ ,在 $ BC $ 段的加速度恒为 $ {a}_{2} $ ,已知物体在 $ A $ 、 $ B $ 、 $ C $ 三点的速度分别为 $ {v}_{A} $ 、 $ {v}_{B} $ 、 $ {v}_{C} $ ,且 $ {v}_{A} < {v}_{C} $ , $ {v}_{B}=\dfrac{{v}_{A}+{v}_{C}}{2} $ .则加速度 $ {a}_{1} $ 和 $ {a}_{2} $ 的大小关系为( )
A. $ {a}_{1} < {a}_{2} $
B. $ {a}_{1}={a}_{2} $
C. $ {a}_{1} > {a}_{2} $
D.条件不足,无法确定
答案:A
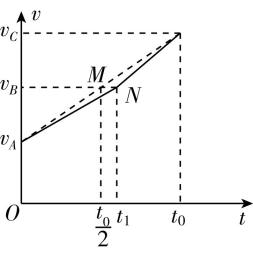
解析:解法一:如图,如果物体做匀加速直线运动,初速度为 $ {v}_{A} $ , $ {t}_{0} $ 时刻速度为 $ {v}_{C} $ ,则 $ \dfrac{{t}_{0}}{2} $ 时刻速度为 $ \dfrac{{v}_{A}+{v}_{C}}{2} $ ,前 $ \dfrac{{t}_{0}}{2} $ 时间内的位移小于 $ {t}_{0} $ 时间内位移的一半,于是将图像上的 $ M $ 点向右平移至 $ N $ 点,使得图示 $ 0\sim {t}_{1} $ 时间内的图线与 $ t $ 轴围成图形的面积等于 $ {t}_{1}\sim {t}_{0} $ 时间内的图线与 $ t $ 轴围成图形的面积.由速度—时间图像中图线的斜率表示加速度可得 $ {a}_{1} < {a}_{2} $ ,故 $ \mathrm{A} $ 正确.
解法二:设物体在 $ AB $ 段和 $ BC $ 段位移均为 $ x $ ,对 $ AB $ 段有 $ {v}_{B}^{2}-{v}_{A}^{2}=2{a}_{1}x $ ,对 $ BC $ 段有 $ {v}_{C}^{2}-{v}_{B}^{2}=2{a}_{2}x $ ,又 $ {v}_{B}=\dfrac{{v}_{A}+{v}_{C}}{2} $ ,得 $ {a}_{2}-{a}_{1}=\dfrac{1}{4x}({v}_{A}-{v}_{C})^{2} $ ,因为物体做变加速直线运动,位移为正,所以 $ {a}_{2} > {a}_{1} $ ,故 $ \mathrm{A} $ 正确.
4.一列火车长为 $ L=200\mathrm{m} $ ,要通过一条长为 $ s=300\mathrm{m} $ 的直隧道,从车头前端刚进入隧道时开始计时,在火车完全驶出隧道前,测得火车运动的平均速度随时间的变化关系为 $ \overline{v}=5+t(\mathrm{m}/\mathrm{s}) $ ,则( )
A.火车头前端刚进入隧道时的瞬时速度大小为 $ 5\mathrm{m}/\mathrm{s} $
B.火车末端刚离开隧道时的瞬时速度大小为 $ 25\mathrm{m}/\mathrm{s} $
C.火车从进入隧道到完全驶出隧道所用时间为 $ 20\mathrm{s} $
D.火车头在穿越隧道的过程中,一直在做匀加速运动,且加速度大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $
答案:AC
解析:由题意可得 $ \dfrac{x}{t}=\overline{v}=5+t(\mathrm{m}/\mathrm{s}) $ ,即 $ x=5t+{t}^{2}(\mathrm{m}) $ ,结合 $ x={v}_{0}t+\dfrac{1}{2}a{t}^{2} $ 可知,加速度 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,初速度为 $ {v}_{0}=5\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 正确, $ \mathrm{D} $ 错误;根据匀变速直线运动的速度—位移公式可得 $ {v}^{2}-{v}_{0}^{2}=2ax\prime $ , $ x\prime =L+s=500\mathrm{m} $ ,解得 $ v=\sqrt{2ax\prime +{v}_{0}^{2}}=45\mathrm{m}/\mathrm{s} $ , $ \mathrm{B} $ 错误;根据匀变速直线运动的速度—时间公式可得 $ t=\dfrac{v-{v}_{0}}{a}=\dfrac{45-5}{2}\mathrm{s}=20\mathrm{s} $ , $ \mathrm{C} $ 正确.
5.如图,某同学将小滑块(可视为质点)以一定的速度 $ v $ 沿水平方向推出,小滑块经 $ a $ 、 $ b $ 、 $ c $ 点后在 $ d $ 点与竖直墙壁发生碰撞,碰撞后原速率弹回,最终停在 $ c $ 点.若 $ ab=bc=cd=l $ ,碰撞时间忽略不计,小滑块整个运动过程中,加速度大小不变,下列说法正确的是( )
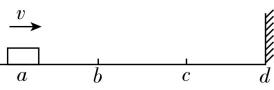
A.小滑块运动的加速度大小为 $ \dfrac{{v}^{2}}{8l} $
B.小滑块运动的总时间为 $ \dfrac{8l}{v} $
C.小滑块从 $ c $ 点运动到 $ d $ 点的时间和从 $ d $ 点运动到 $ c $ 点的时间之比为 $ 1:\sqrt{2} $
D.小滑块与竖直墙壁碰撞前的瞬时速度大小为 $ \dfrac{v}{2} $
答案:ABD
解析:小滑块由 $ a $ 运动到 $ d $ 与墙壁发生碰撞后停在 $ c $ 点,可等效为小滑块一直沿水平方向运动到 $ e $ 点,如图所示, $ e $ 点与 $ c $ 点关于墙壁对称,根据 $ {v}^{2}=2a\cdot 4l $ ,解得 $ a=\dfrac{{v}^{2}}{8l} $ , $ \mathrm{A} $ 正确;小滑块运动的总时间为 $ t=\dfrac{v}{a}=\dfrac{8l}{v} $ , $ \mathrm{B} $ 正确;根据逆向思维结合初速度为零的匀加速直线运动的推论,小滑块从 $ c $ 点运动到 $ d $ 点的时间和从 $ d $ 点运动到 $ c $ 点的时间之比为 $ (\sqrt{2}-1):1 $ , $ \mathrm{C} $ 错误;根据 $ {v}^{2}-{v}_{1}^{2}=2a\cdot 3l $ ,解得 $ {v}_{1}=\dfrac{v}{2} $ , $ \mathrm{D} $ 正确.
6.如图为某质点在 $ t=0 $ 时刻在外力作用下由静止开始做匀变速直线运动的速度平方 $ {v}^{2} $ 与位置坐标 $ x $ 的关系图像,则下列说法正确的是( )

A.质点的加速度大小为 $ 0.5\mathrm{m}/{\mathrm{s}}^{2} $
B.质点的加速度大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $
C.质点在 $ t=4\mathrm{s} $ 时坐标为 $ x=4\mathrm{m} $
D.质点在 $ t=4\mathrm{s} $ 时坐标为 $ x=2\mathrm{m} $
答案:AD
解析:质点由静止开始做匀变速直线运动,由 $ {v}^{2}=2a(x-{x}_{0}) $ 可知,在 $ {v}^{2}-x $ 图像中,图线斜率 $ k=2a $ ,解得质点的加速度大小为 $ a=0.5\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;质点的初始位置坐标为 $ {x}_{0} $ ,代入 $ (0,2{\mathrm{m}}^{2}/{\mathrm{s}}^{2}) $ ,得 $ {x}_{0}=-2\mathrm{m} $ ,当 $ t=4\mathrm{s} $ 时,质点的坐标为 $ x $ ,则 $ x-{x}_{0}=\dfrac{1}{2}a{t}^{2} $ ,得 $ x=2\mathrm{m} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
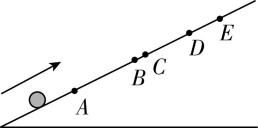
7.如图所示,小球沿足够长的固定斜面以初速度 $ v $ 向上做匀减速直线运动,依次通过 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 到达最高点 $ E $ ,已知 $ {x}_{AB}={x}_{BD}=6\mathrm{m} $ , $ {x}_{BC}=1\mathrm{m} $ ,小球从 $ A $ 到 $ C $ 和从 $ C $ 到 $ D $ 所用时间均为 $ 2\mathrm{s} $ ,则( )
A.小球向上运动过程中加速度大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $
B.小球经过 $ A $ 点时的速度大小为 $ 4\mathrm{m}/\mathrm{s} $
C.小球在 $ AE $ 段的平均速度大小为 $ 3\mathrm{m}/\mathrm{s} $
D.小球从 $ D $ 到 $ E $ 的时间为 $ 4\mathrm{s} $
答案:BD
解析:小球从 $ A $ 经 $ C $ 到 $ D $ 过程,根据 $ {x}_{AC}-{x}_{CD}=a{T}^{2} $ ,代入数据解得 $ a=0.5\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{A} $ 错误;小球经过 $ C $ 点的速度等于在 $ AD $ 段的平均速度,则 $ {v}_{C}=\dfrac{{x}_{AD}}{2T}=3\mathrm{m}/\mathrm{s} $ ,又由于 $ {v}_{A}^{2}-{v}_{C}^{2}=2a{x}_{AC} $ ,代入数据解得 $ {v}_{A}=4\mathrm{m}/\mathrm{s} $ , $ \mathrm{B} $ 正确;由于到达 $ E $ 点时速度减为零,因此小球在 $ AE $ 段的平均速度大小 $ \overline{v}=\dfrac{{v}_{A}+{v}_{E}}{2}=2\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 错误;小球从 $ C $ 到 $ E $ 的时间为 $ t=\dfrac{{v}_{C}}{a}=6\mathrm{s} $ ,从 $ C $ 到 $ D $ 的时间为 $ 2\mathrm{s} $ ,因此小球从 $ D $ 到 $ E $ 的时间为 $ 4\mathrm{s} $ , $ \mathrm{D} $ 正确.
8.在高速公路上甲、乙两轿车发生了追尾事故,交警部门用拖车一起拖拽两车,从静止开始做近似匀加速直线运动,甲、乙两轿车运动的 $ \dfrac{x}{t}-t $ 和 $ {v}^{2}-x $ 图像分别如图甲、乙所示,则下列说法正确的是( )
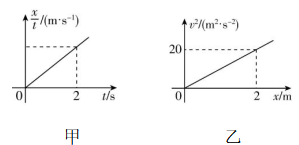
A.图乙的斜率大小是图甲的斜率大小的2倍
B.甲的加速度大小为 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $
C.前 $ 2\mathrm{m} $ 位移的中间时刻的速度大小为 $ \dfrac{\sqrt{5}}{2}\mathrm{m}/\mathrm{s} $
D.前 $ 2\mathrm{s} $ 内的中点位置的速度大小为 $ 5\sqrt{2}\mathrm{m}/\mathrm{s} $
答案:D
解析:根据 $ x=\dfrac{1}{2}a{t}^{2} $ ,可得 $ \dfrac{x}{t}=\dfrac{1}{2}at $ ,则题图甲图像的斜率 $ {k}_{1}=\dfrac{1}{2}a $ ,根据 $ {v}^{2}=2ax $ ,则题图乙图像的斜率 $ {k}_{2}=2a $ ,则 $ a=5\mathrm{m}/{\mathrm{s}}^{2} $ ,由此可知,题图乙的斜率大小是题图甲的斜率大小的4倍,甲车的加速度大小为 $ 5\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;前 $ 2\mathrm{m} $ 位移的总时间 $ {t}_{1}=\sqrt{\dfrac{2{x}_{1}}{a}}=\dfrac{2}{\sqrt{5}}\mathrm{s} $ ,则中间时刻的速度大小为 $ {v}_{\frac{t}{2}}=a\dfrac{{t}_{1}}{2}=\sqrt{5}\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 错误;前 $ 2\mathrm{s} $ 内的位移大小 $ {x}_{2}=\dfrac{1}{2}a{t}_{2}^{2}=\dfrac{1}{2}×5×{2}^{2}\mathrm{m}=10\mathrm{m} $ ,中点位置的速度大小为 $ {v}_{\frac{x}{2}}=\sqrt{2a\dfrac{{x}_{2}}{2}}=5\sqrt{2}\mathrm{m}/\mathrm{s} $ , $ \mathrm{D} $ 正确.
9.如图,假设在发生山体滑坡时,距离山坡底部 $ A $ 处 $ {x}_{0}=36\mathrm{m} $ 的 $ B $ 点正有一行人逗留,此时距坡底 $ {x}_{1}=50\mathrm{m} $ (斜坡长度)的山坡顶处有一大片泥石流正以大小为 $ {a}_{1}=4\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度由静止开始沿斜坡匀加速下滑,泥石流的宽度为 $ L=36\mathrm{m} $ ,行人发现后准备加速逃离.已知行人从发现泥石流到开始逃离的反应时间为 $ \mathrm{\Delta }t=1\mathrm{s} $ ,之后行人以大小为 $ {a}_{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度由静止开始做匀加速直线运动,跑动的最大速度为 $ {v}_{\mathrm{m}}=8\mathrm{m}/\mathrm{s} $ ,达到最大速度后做匀速直线运动.泥石流滑到坡底前后速度大小不变,但滑到水平面时开始以大小为 $ {a}_{3}=2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度做匀减速直线运动,泥石流始终平行于 $ AC $ 边.
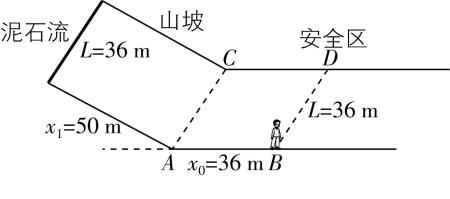
(1) 求泥石流在山坡上的运动时间及到达坡底时的速度大小;
(2) 若行人沿 $ BD $ 方向逃离, $ BD $ 边平行于坡底 $ AC $ 边,过 $ D $ 点后为安全区,请判断行人是否能到达安全区?若能,求行人从开始运动至到达安全区的时间;若不能,求行人被泥石流撞上的位置与 $ D $ 点的距离.
答案:(1) $ 5\mathrm{s} $ ; $ 20\mathrm{m}/\mathrm{s} $
(2) 不能; $ 4\mathrm{m} $
解析:(1) 泥石流在山坡上做匀加速直线运动,由运动学公式有 $ {x}_{1}=\dfrac{1}{2}{a}_{1}{t}_{1}^{2} $ , $ {v}_{1}={a}_{1}{t}_{1} $ ,联立解得泥石流在山坡上的运动时间为 $ {t}_{1}=5\mathrm{s} $ ,泥石流到达坡底时的速度大小为 $ {v}_{1}=20\mathrm{m}/\mathrm{s} $ .
(2) 泥石流滑到水平面后做匀减速直线运动,则 $ {x}_{0}={v}_{1}{t}_{2}-\dfrac{1}{2}{a}_{3}{t}_{2}^{2} $ ,解得 $ {t}_{2}=2\mathrm{s} $ 或 $ {t}_{2}=18\mathrm{s} $ (舍去),行人沿 $ BD $ 方向做匀加速直线运动期间,有 $ {x}_{2}=\dfrac{{v}_{\mathrm{m}}^{2}}{2{a}_{2}}=16\mathrm{m} $ , $ {t}_{3}=\dfrac{{v}_{\mathrm{m}}}{{a}_{2}}=4\mathrm{s} $ ,匀速运动的时间为 $ {t}_{4}=\dfrac{L-{x}_{2}}{{v}_{\mathrm{m}}}=2.5\mathrm{s} $ ,由于 $ \mathrm{\Delta }t+{t}_{3}+{t}_{4}=7.5\mathrm{s} > {t}_{1}+{t}_{2}=7\mathrm{s} $ ,说明行人不能到达安全区,行人被泥石流撞上的位置与 $ D $ 点的距离为 $ x={v}_{\mathrm{m}}(\mathrm{\Delta }t+{t}_{3}+{t}_{4}-{t}_{1}-{t}_{2})=4\mathrm{m} $ .