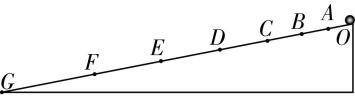
2.自动配餐小车沿一条直线运动依次通过 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 四点,如图所示.小车从 $ A $ 到 $ C $ 做匀加速直线运动,在 $ C $ 点开始刹车做匀减速直线运动,在 $ D $ 点恰好停止,已知 $ {x}_{AB}=4\mathrm{m} $ ,通过 $ AB $ 段所用时间为 $ 1\mathrm{s} $ , $ {x}_{BC}=14\mathrm{m} $ ,通过 $ BC $ 段所用时间为 $ 2\mathrm{s} $ , $ {x}_{CD}=9\mathrm{m} $ ,则小车加速和减速过程的加速度大小分别为( )

A. $ 2\mathrm{m}/{\mathrm{s}}^{2} $ , $ 3\mathrm{m}/{\mathrm{s}}^{2} $
B. $ 4\mathrm{m}/{\mathrm{s}}^{2} $ , $ 3\mathrm{m}/{\mathrm{s}}^{2} $
C. $ 2\mathrm{m}/{\mathrm{s}}^{2} $ , $ 4.5\mathrm{m}/{\mathrm{s}}^{2} $
D. $ 4\mathrm{m}/{\mathrm{s}}^{2} $ , $ 4.5\mathrm{m}/{\mathrm{s}}^{2} $
小车在 $ AB $ 段的平均速度等于 $ AB $ 段中间时刻的瞬时速度,则 $ {v}_{1}={\overline{v}}_{AB}=\dfrac{{x}_{AB}}{{t}_{1}}=4\mathrm{m}/\mathrm{s} $ ,小车在 $ BC $ 段的平均速度等于 $ BC $ 段中间时刻的瞬时速度,则 $ {v}_{2}={\overline{v}}_{BC}=\dfrac{{x}_{BC}}{{t}_{2}}=7\mathrm{m}/\mathrm{s} $ ,则加速过程的加速度 $ {a}_{1}=\dfrac{{v}_{2}-{v}_{1}}{\dfrac{{t}_{1}+{t}_{2}}{2}}=\dfrac{7-4}{1.5}\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,到达 $ C $ 点时的速度 $ {v}_{C}={v}_{2}+{a}_{1}\frac{{t}_{2}}{2}=(7+2×1)\mathrm{m}/\mathrm{s}=9\mathrm{m}/\mathrm{s} $ ,减速过程的加速度大小 $ {a}_{2}=\dfrac{{v}_{C}^{2}}{2{x}_{CD}}=\dfrac{{9}^{2}}{2×9}\mathrm{m}/{\mathrm{s}}^{2}=4.5\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{C} $ 正确.

 (多选)
(多选)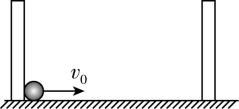 (多选)
(多选)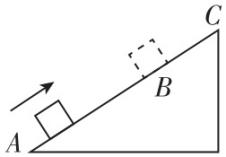


 (多选)
(多选)