专题3 追及与相遇问题
一、刷题型
1.在十字路口,汽车以大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度从停止线启动后匀加速行驶,刚启动时恰好有一辆电动车以大小为 $ 10\mathrm{m}/\mathrm{s} $ 的速度匀速驶过停止线与汽车同方向行驶,两车均做直线运动.下列说法正确的是( )
A.汽车追上电动车之前,汽车已运动 $ 20\mathrm{s} $ 时它们相距最远
B.汽车追上电动车之前,它们的最远距离为 $ 25\mathrm{m} $
C.汽车在距停止线 $ 100\mathrm{m} $ 处追上电动车
D.汽车追上电动车时的速度大小为 $ 20\mathrm{m}/\mathrm{s} $
答案:D
解析:当两车速度相等时相距最远,设所用时间为 $ t $ ,汽车做初速度为0的匀加速直线运动,有 $ {v}_{汽}=at={v}_{电}=10\mathrm{m}/\mathrm{s} $ ,可得 $ t=10\mathrm{s} $ ,则两车最远距离为 $ \mathrm{\Delta }x={x}_{电}-{x}_{汽}={v}_{电}t-\dfrac{{v}_{汽}}{2}t=50\mathrm{m} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;汽车追上电动车时,它们相对于停止线的位移相等,设汽车追上电动车所用时间为 $ t\prime $ ,此时有 $ {v}_{电}t\prime =\dfrac{1}{2}at{\prime }^{2} $ ,解得 $ t\prime =20\mathrm{s} $ ,此时汽车距停止线距离为 $ x={v}_{电}t\prime =200\mathrm{m} $ ,此时汽车速度为 $ {v}_{汽}=at\prime =20\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
2.甲、乙两辆智能巴士在同一水平直道上运动,其运动的位置—时间图像如图所示,则( )

A.甲车在 $ 0\mathrm{~}8\mathrm{s} $ 内的平均速度大小为 $ 2\mathrm{m}/\mathrm{s} $
B. $ 0\mathrm{~}8\mathrm{s} $ 内,乙车做曲线运动
C.在 $ 8\mathrm{s} $ 末甲车追上乙车,两车相遇
D.若乙车做初速度为0的匀加速直线运动,则乙车的加速度为 $ 0.5\mathrm{m}/{\mathrm{s}}^{2} $
答案:D
解析:甲车在 $ 0\mathrm{~}8\mathrm{s} $ 内的平均速度大小为 $ \overline{v}=\dfrac{16-4}{8}\mathrm{m}/\mathrm{s}=1.5\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 错误;位置—时间图像只能描述直线运动,则 $ 0\mathrm{~}8\mathrm{s} $ 内,乙车做直线运动, $ \mathrm{B} $ 错误;由题图可知, $ t=0 $ 时,甲车在前, $ t=8\mathrm{s} $ 时两车位置相同,则在 $ 8\mathrm{s} $ 末乙车追上甲车, $ \mathrm{C} $ 错误;若乙车做初速度为0的匀加速直线运动,则乙车的加速度为 $ a=\dfrac{2x}{{t}^{2}}=\dfrac{2×16}{{8}^{2}}\mathrm{m}/{\mathrm{s}}^{2}=0.5\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{D} $ 正确.
3.蓝牙耳机无线连接的最远距离为 $ 10\mathrm{m} $ .甲和乙两位同学做了一个有趣的实验:如图(a)所示,甲佩戴蓝牙耳机,乙携带手机检测,甲、乙在同一条直道上,相距 $ 2\mathrm{m} $ ,同时向右运动,甲做匀速直线运动,乙从静止开始先做匀加速直线运动,再做匀速直线运动,甲、乙的速度 $ v $ 与时间 $ t $ 的关系如图(b)所示,则在运动过程中,手机检测到蓝牙耳机能被连接的总时间为( )
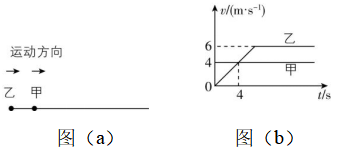
A. $ 13\mathrm{s} $
B. $ 14\mathrm{s} $
C. $ 15\mathrm{s} $
D. $ 16\mathrm{s} $
答案:C
解析:根据题图(b)知,第 $ 4\mathrm{s} $ 时甲、乙速度相等,则前 $ 4\mathrm{s} $ 内甲、乙的距离增大,第 $ 4\mathrm{s} $ 时距离最大,由 $ v-t $ 图像可得 $ t=4\mathrm{s} $ 时 $ {x}_{甲}=4×4\mathrm{m}=16\mathrm{m} $ , $ {x}_{乙}=\dfrac{1}{2}×4×4\mathrm{m}=8\mathrm{m} $ ,则第 $ 4\mathrm{s} $ 时二者相距 $ s=16\mathrm{m}+2\mathrm{m}-8\mathrm{m}=10\mathrm{m} $ ,故前 $ 4\mathrm{s} $ 内蓝牙耳机能被连接;第 $ 4\mathrm{s} $ 后乙的速度超过甲,二者距离减小,至第 $ 6\mathrm{s} $ 时,有 $ x{\prime }_{甲}=4×6\mathrm{m}=24\mathrm{m} $ , $ x{\prime }_{乙}=\dfrac{1}{2}×6×6\mathrm{m}=18\mathrm{m} $ ,第 $ 6\mathrm{s} $ 时二者相距 $ s\prime =24\mathrm{m}+2\mathrm{m}-18\mathrm{m}=8\mathrm{m} $ ,此后二者均做匀速直线运动,设乙追上甲并超过甲 $ 10\mathrm{m} $ 需要的时间为 $ t\prime $ ,则有 $ 6\mathrm{m}/\mathrm{s}×t\prime -4\mathrm{m}/\mathrm{s}×t\prime =8\mathrm{m}+10\mathrm{m} $ ,解得 $ t\prime =9\mathrm{s} $ ,则手机检测到蓝牙耳机能被连接的总时间为 $ 6\mathrm{s}+9\mathrm{s}=15\mathrm{s} $ ,故选 $ \mathrm{C} $ .
4.甲、乙两个物体沿同一方向做直线运动,乙的出发点在甲前方 $ 6\mathrm{m} $ 处,其 $ v-t $ 图像如图所示.关于两物体的运动情况,下列说法正确的是( )

A.在 $ t=2\mathrm{s} $ 时,甲的速度方向发生改变
B.在 $ t=4\mathrm{s} $ 时,甲、乙相遇
C. $ 0\sim 6\mathrm{s} $ 内,甲、乙的平均速度相同
D.在 $ t=3\mathrm{s} $ 时,甲在乙前方
答案:B
解析:由 $ v-t $ 图像可知, $ 0\sim 6\mathrm{s} $ 内,甲的速度一直为正方向,所以在 $ t=2\mathrm{s} $ 时,甲的速度方向没有发生改变,故 $ \mathrm{A} $ 错误;根据 $ v-t $ 图像与横轴围成的图形面积表示位移,可知 $ 0\sim 4\mathrm{s} $ 内,甲、乙通过的位移分别为 $ {x}_{甲}=\dfrac{1}{2}×6×2\mathrm{m}+\dfrac{1}{2}×(6+3)×2\mathrm{m}=15\mathrm{m} $ , $ {x}_{乙}=3×2\mathrm{m}+\dfrac{1}{2}×3×2\mathrm{m}=9\mathrm{m} $ ,有 $ \mathrm{\Delta }x={x}_{甲}-{x}_{乙}=15\mathrm{m}-9\mathrm{m}=6\mathrm{m} $ ,由于乙的出发点在甲前方 $ 6\mathrm{m} $ 处,可知在 $ t=4\mathrm{s} $ 时,甲、乙相遇,由于 $ 3\sim 4\mathrm{s} $ 内甲的速度大于乙的速度,所以在 $ t=3\mathrm{s} $ 时,甲在乙后方,故 $ \mathrm{B} $ 正确, $ \mathrm{D} $ 错误; $ 0\sim 6\mathrm{s} $ 内,甲、乙通过的位移分别为 $ x{\prime }_{甲}=\dfrac{1}{2}×6×6\mathrm{m}=18\mathrm{m} $ 、 $ x{\prime }_{乙}=3×2\mathrm{m}+\dfrac{1}{2}×3×2\mathrm{m}-\dfrac{1}{2}×3×2\mathrm{m}=6\mathrm{m} $ ,由于 $ 0\sim 6\mathrm{s} $ 内,甲、乙通过的位移不相等,所以甲、乙的平均速度不相同,故 $ \mathrm{C} $ 错误.
5.一辆小汽车以 $ 30\mathrm{m}/\mathrm{s} $ 的速度匀速行驶在高速公路上,突然发现正前方 $ 30\mathrm{m} $ 处有一辆大卡车以 $ 10\mathrm{m}/\mathrm{s} $ 的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵,如图所示,图线 $ a $ 、 $ b $ 分别为小汽车和大卡车的 $ v-t $ 图像(忽略刹车反应时间),以下说法正确的是( )
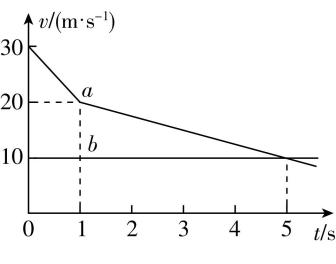
A.因刹车失灵前小汽车已减速,故不会发生追尾事故
B.在 $ t=4\mathrm{s} $ 时发生追尾事故
C.在 $ t=5\mathrm{s} $ 时发生追尾事故
D.若紧急刹车时两车相距 $ 40\mathrm{m} $ ,则不会发生追尾事故且两车最近时相距 $ 5\mathrm{m} $
答案:D
解析:根据速度—时间图线与时间轴所围面积大小等于位移大小,由题图知, $ t=3\mathrm{s} $ 时大卡车的位移为 $ {x}_{b}={v}_{b}t=10×3\mathrm{m}=30\mathrm{m} $ ,小汽车的位移为 $ {x}_{a}=\dfrac{1}{2}×(30+20)×1\mathrm{m}+\dfrac{1}{2}×(20+15)×2\mathrm{m}=60\mathrm{m} $ ,则 $ {x}_{a}-{x}_{b}=30\mathrm{m} $ ,所以在 $ t=3\mathrm{s} $ 时发生追尾事故,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误;由 $ v-t $ 图线可知在 $ t=5\mathrm{s} $ 时两车速度相等,小汽车相对于大卡车的位移 $ \mathrm{\Delta }x=\dfrac{1}{2}×(20+10)×1\mathrm{m}+\dfrac{1}{2}×10×4\mathrm{m}=35\mathrm{m} < 40\mathrm{m} $ ,则不会发生追尾事故,且两车最近时相距 $ \mathrm{\Delta }s={x}_{0}-\mathrm{\Delta }x=5\mathrm{m} $ ,故 $ \mathrm{D} $ 正确.
6.一辆汽车以 $ 54\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度在平直的公路上做匀速直线运动,在它的正前方有一辆自行车以 $ 25.2\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度同向匀速行驶,汽车驾驶员发现自行车后经 $ 0.4\mathrm{s} $ 踩下刹车,汽车以大小为 $ 5\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度做匀减速直线运动.若汽车和自行车均可视为质点,要使汽车不碰上自行车,驾驶员发现自行车时汽车到自行车的距离至少为( )
A. $ 9.6\mathrm{m} $
B. $ 6.4\mathrm{m} $
C. $ 4.7\mathrm{m} $
D. $ 2.8\mathrm{m} $
答案:A
解析:设汽车减速时间为 $ t $ ,驾驶员反应时间为 $ \mathrm{\Delta }t $ ,驾驶员发现自行车时汽车到自行车的距离为 $ s $ .若汽车刚追上自行车时,二者速度刚好相等,则汽车恰好不会碰上自行车.此时二者的位移关系有 $ s+{v}_{自}(t+\mathrm{\Delta }t)={v}_{汽}\mathrm{\Delta }t+{v}_{汽}t-\dfrac{1}{2}a{t}^{2} $ ,由速度关系有 $ {v}_{自}={v}_{汽}-at $ ,联立解得 $ s=9.6\mathrm{m} $ ,故选 $ \mathrm{A} $ .
7.如图所示,一颗松子沿倾斜冰面 $ AB $ 从顶端 $ A $ 点由静止匀加速滑下, $ 1\mathrm{s} $ 后松鼠从 $ A $ 点以 $ 1.5\mathrm{m}/\mathrm{s} $ 的初速度、 $ 3\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度沿直线匀加速追赶松子.追赶过程中,松鼠与松子相隔的最远距离为 $ \dfrac{9}{8}\mathrm{m} $ ,且松鼠恰好在冰面底端 $ B $ 点追上松子,则( )
 (多选)
(多选)
A.松子沿冰面下滑的加速度大小为 $ 4\mathrm{m}/{\mathrm{s}}^{2} $
B.冰面 $ AB $ 的长度为 $ 9\mathrm{m} $
C.松鼠从 $ A $ 点出发后,经过 $ 2\mathrm{s} $ 追上松子
D.在松鼠与松子相隔最远时,松鼠的速度大小为 $ 6\mathrm{m}/\mathrm{s} $
答案:BC
解析:松鼠与松子相隔的距离最远时,松鼠与松子速度相等,设此时松子运动时间为 $ t $ ,松子沿冰面下滑的加速度大小为 $ {a}_{1} $ ,松鼠的加速度大小为 $ {a}_{2} $ ,有 $ {a}_{1}t={v}_{0}+{a}_{2}(t-1\mathrm{s}) $ , $ \dfrac{1}{2}{a}_{1}{t}^{2}={v}_{0} (t-1\mathrm{s} )+\dfrac{1}{2}{a}_{2} (t-1\mathrm{s})^{2}+{d}_{\mathrm{m}} $ ,联立解得 $ {a}_{1}=2\mathrm{m}/{\mathrm{s}}^{2} $ , $ t=1.5\mathrm{s} $ ,在松鼠与松子相隔最远时,松鼠的速度大小为 $ v={a}_{1}t=2×1.5\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{D} $ 错误;设松子运动时间为 $ {t}_{1} $ 时,松鼠追上松子,有 $ \dfrac{1}{2}{a}_{1}{t}_{1}^{2}={v}_{0} ({t}_{1}-1\mathrm{s} )+\dfrac{1}{2}{a}_{2}\cdot ({t}_{1}-1\mathrm{s})^{2} $ ,解得 $ {t}_{1}=3\mathrm{s} $ ,冰面 $ AB $ 的长度为 $ {l}_{AB}=\dfrac{1}{2}{a}_{1}{t}_{1}^{2}=\dfrac{1}{2}×2×{3}^{2}\mathrm{m}=9\mathrm{m} $ ,故 $ \mathrm{B} $ 正确;松鼠从顶端 $ A $ 出发后,追上松子所用时间为 $ {t}_{2}={t}_{1}-1\mathrm{s}=3\mathrm{s}-1\mathrm{s}=2\mathrm{s} $ ,故 $ \mathrm{C} $ 正确.
8.如图1,甲、乙两车在同一平直道路上,甲车以速度 $ {v}_{0}=36\mathrm{m}/\mathrm{s} $ 匀速行驶,乙车停在路边.甲车在乙车后 $ {s}_{0}=54\mathrm{m} $ 处时,甲车开始匀减速运动准备停车.已知从甲车减速时开始计时,第1秒内位移为 $ {x}_{1}=32\mathrm{m} $ .从甲车减速开始1秒末乙车开始运动,与甲车同向行驶,其速度—时间图像如图2所示,甲、乙相遇时会错车而过,不会相撞.求:
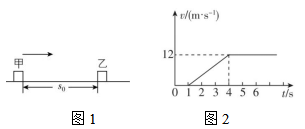
(1) 甲车减速时的加速度大小;
(2) 甲刚停下时,两车相距多远;
(3) 甲、乙两车相遇的时间.
答案:(1) $ 8\mathrm{m}/{\mathrm{s}}^{2} $
(2) $ 3\mathrm{m} $
(3) $ 2\mathrm{s} $ 和 $ 4.75\mathrm{s} $
解析:(1) 甲车刚减速第1秒内有 $ {x}_{1}={v}_{0}t+\dfrac{1}{2}{a}_{1}{t}^{2} $ ,解得 $ {a}_{1}=-8\mathrm{m}/{\mathrm{s}}^{2} $ ,即甲车减速时的加速度大小为 $ 8\mathrm{m}/{\mathrm{s}}^{2} $ .
(2) 甲车减速阶段的位移为 $ {x}_{甲}=\dfrac{0-{v}_{0}^{2}}{2{a}_{1}} $ ,减速至零的时间为 $ {t}_{1}=\dfrac{0-{v}_{0}}{{a}_{1}}=4.5\mathrm{s} $ ,设乙车加速度为 $ {a}_{2} $ ,由图像可得 $ {a}_{2}=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=4\mathrm{m}/{\mathrm{s}}^{2} $ ,乙车做匀加速直线运动的时间为 $ {t}_{2}=3\mathrm{s} $ ,甲车停下来的过程中乙车的位移为 $ {x}_{乙}=\dfrac{1}{2}{a}_{2}{t}_{2}^{2}+{v}_{乙}({t}_{1}-{t}_{2}-1\mathrm{s}) $ ,联立解得 $ {x}_{甲}=81\mathrm{m} $ , $ {x}_{乙}=24\mathrm{m} $ ,故两车相距 $ \mathrm{\Delta }x={x}_{甲}-({x}_{乙}+{s}_{0})=3\mathrm{m} $ .
(3) 由题意和以上结果可知,设从甲减速开始经过 $ {t}_{3} $ ,甲、乙两车相遇, $ x{\prime }_{甲}={v}_{0}{t}_{3}+\dfrac{1}{2}{a}_{1}{t}_{3}^{2} $ , $ x{\prime }_{乙}=\dfrac{1}{2}{a}_{2}({t}_{3}-1\mathrm{s})^{2} $ ,两车相遇,有 $ x{\prime }_{甲}=x{\prime }_{乙}+{s}_{0} $ ,解得 $ {t}_{3}=2\mathrm{s} $ 或 $ {t}_{3}=\dfrac{14}{3}\mathrm{s} $ (甲车已经停下,不合理,舍去),甲、乙还会第二次相遇, $ \mathrm{\Delta }x={v}_{乙}{t}_{4} $ ,解得 $ {t}_{4}=0.25\mathrm{s} $ ,甲、乙第二次相遇时间为 $ {t}_{5}={t}_{4}+{t}_{1}=4.75\mathrm{s} $ .
9.如图所示为某地的转盘路,汽车要想直行,到转盘路时,需要先做半径为 $ R=25\mathrm{m} $ 的圆周运动,运动半个圆周后再直行.若汽车甲到达转盘路时,汽车乙恰好通过转盘路进入直行车道,以 $ v=30\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度匀速行驶.已知汽车通过转盘路过程的速度不能超过 $ v=30\mathrm{k}\mathrm{m}/\mathrm{h} $ ,通过后在直行车道上的速度不能超过 $ v\prime =72\mathrm{k}\mathrm{m}/\mathrm{h} $ ,加速度不能超过 $ a=4\mathrm{m}/{\mathrm{s}}^{2} $ ,则汽车甲追上汽车乙所用的最短时间约为(假设直行车道足够长,且没有通过红绿灯,另外不考虑汽车的变加速恒功率过程)( )

A. $ 15.7\mathrm{s} $
B. $ 17.6\mathrm{s} $
C. $ 19.5\mathrm{s} $
D. $ 21.4\mathrm{s} $
答案:B
解析:汽车甲到达转盘路时速度为 $ v=30\mathrm{k}\mathrm{m}/\mathrm{h} $ ,通过转盘路的时间为 $ {t}_{1}=\dfrac{\mathrm{\pi }R}{v}\approx 9.42\mathrm{s} $ ,直线加速时间 $ {t}_{2}=\dfrac{v\prime -v}{a}=2.92\mathrm{s} $ ,假设甲匀速后追上乙,则此时 $ v{t}_{1}+\dfrac{v+v\prime }{2}{t}_{2}+v\prime t=\mathrm{\pi }R+v({t}_{1}+{t}_{2}+t) $ ,解得 $ t\approx 5.27\mathrm{s} $ ,假设成立,则汽车甲追上汽车乙所用的最短时间约为 $ {t}_{1}+{t}_{2}+t=17.6\mathrm{s} $ ,故选 $ \mathrm{B} $ .
10.甲、乙两车在同一平直公路上向右匀速行驶,甲车的速度为 $ {v}_{1}=16\mathrm{m}/\mathrm{s} $ ,乙车的速度为 $ {v}_{2}=12\mathrm{m}/\mathrm{s} $ ,乙车在甲车的前面.当两车相距 $ L=6\mathrm{m} $ 时,两车同时开始刹车,从此时开始计时,甲车以加速度大小为 $ {a}_{1}=2\mathrm{m}/{\mathrm{s}}^{2} $ 刹车, $ 6\mathrm{s} $ 后立即改做匀速直线运动,乙车刹车的加速度大小为 $ {a}_{2}=1\mathrm{m}/{\mathrm{s}}^{2} $ .求:
(1) 从两车刹车开始计时,甲车第一次追上乙车所用的时间;
(2) 两车相遇的次数;
(3) 两车速度相等的时间.
答案:(1) $ 2\mathrm{s} $
(2) 3次
(3) $ 4\mathrm{s} $ 和 $ 8\mathrm{s} $
解析:(1) 从两车刹车开始计时,设甲车第一次追上乙车所用时间为 $ t $ ,则有 $ {v}_{1}t-\dfrac{1}{2}{a}_{1}{t}^{2}={v}_{2}t-\dfrac{1}{2}{a}_{2}{t}^{2}+L $ ,解得 $ {t}_{1}=2\mathrm{s} $ , $ {t}_{2}=6\mathrm{s} $ ,所以在 $ {t}_{1}=2\mathrm{s} $ 时甲车第一次追上乙车.
(2) 当 $ {t}_{2}=6\mathrm{s} $ 时,甲车的速度大小为 $ v{\prime }_{1}={v}_{1}-{a}_{1}{t}_{2}=4\mathrm{m}/\mathrm{s} $ ,此后甲车一直匀速运动,乙车的速度大小为 $ v{\prime }_{2}={v}_{2}-{a}_{2}{t}_{2}=6\mathrm{m}/\mathrm{s} $ ,此时乙车追上甲车,甲车的速度小于乙车的速度,但乙车做减速运动,假设再经 $ \mathrm{\Delta }t $ 后甲车追上乙车,有 $ v{\prime }_{1}\cdot \mathrm{\Delta }t=v{\prime }_{2}\cdot \mathrm{\Delta }t-\dfrac{1}{2}{a}_{2}(\mathrm{\Delta }t)^{2} $ ,解得 $ \mathrm{\Delta }t=4\mathrm{s} < \dfrac{v{\prime }_{2}}{{a}_{2}} $ ,此时乙车仍在做减速运动,假设成立,综合以上分析知,甲、乙两车共相遇3次.
(3) 设两车第一次速度相等的时间为 $ {t}_{3} $ ,有 $ {v}_{1}-{a}_{1}{t}_{3}={v}_{2}-{a}_{2}{t}_{3} $ ,解得 $ {t}_{3}=4\mathrm{s} $ ,甲车匀速运动的速度为 $ 4\mathrm{m}/\mathrm{s} $ ,设第二次速度相等的时间为 $ {t}_{4} $ ,有 $ v{\prime }_{1}={v}_{2}-{a}_{2}{t}_{4} $ ,解得 $ {t}_{4}=8\mathrm{s} $ .




 (多选)
(多选)
