第4节 自由落体运动
一、刷基础
1.关于玻璃管内羽毛、铁片下落演示实验对比的结论,下列选项正确的是( )

A.物体下落的快慢跟它的轻重有关
B.把玻璃管内的空气抽出去,铁片下落得更慢了
C.把玻璃管内的空气抽出去,是为了减小空气阻力的影响
D.在现实生活中如果没有空气阻力,所有物体下落的快慢都不一样
答案:C
解析:物体下落的快慢跟它的轻重无关,故 $ \mathrm{A} $ 错误;把玻璃管内的空气抽出去,铁片下落得更快了,故 $ \mathrm{B} $ 错误;把玻璃管内的空气抽出去,是为了减小空气阻力的影响,故 $ \mathrm{C} $ 正确;在现实生活中如果没有空气阻力,所有物体下落的快慢都一样,故 $ \mathrm{D} $ 错误.
2.如图所示,在长为 $ 1.8\mathrm{m} $ 的轻绳的两端各拴一个小球 $ A $ 、 $ B $ (均可视为质点),用手捏住 $ A $ 、 $ B $ 竖直悬挂,站在某一高处,某时刻由静止释放,测得 $ B $ 、 $ A $ 两球先后落地的时间差为 $ 0.2\mathrm{s} $ ,不计空气阻力,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .则小球 $ A $ 的释放点到地面的高度为( )
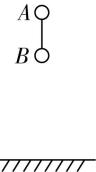
A. $ 4.8\mathrm{m} $
B. $ 5\mathrm{m} $
C. $ 5.6\mathrm{m} $
D. $ 6\mathrm{m} $
答案:B
解析:设小球 $ A $ 落地时间为 $ t $ ,有 $ {ℎ}_{AB}=\dfrac{1}{2}g{t}^{2}-\dfrac{1}{2}g(t-0.2\mathrm{s})^{2} $ ,解得 $ t=1\mathrm{s} $ ,则小球 $ A $ 释放点离地高度为 $ {ℎ}_{A}=\dfrac{1}{2}g{t}^{2}=5\mathrm{m} $ ,故 $ \mathrm{B} $ 正确.
3.某幢楼房每层楼的高度都为 $ ℎ $ ,一小石子从天台最边缘无初速度落下.如图所示, $ OA $ 段为楼房的顶层, $ BC $ 段为楼房的最下面5层,已知小石子通过图中 $ OA $ 段的时间和通过 $ BC $ 段的时间相等,若不计空气阻力,小石子可视为质点,则该楼房的层数为( )
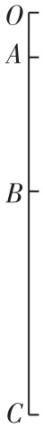
A.8
B.9
C.10
D.12
答案:B
解析:设小石子经过 $ OA $ 段和 $ BC $ 段的时间均为 $ t $ ,则小石子经过 $ OA $ 段中间时刻的速度大小为 $ {v}_{1}=\dfrac{ℎ}{t} $ ,经过 $ BC $ 段中间时刻的速度大小为 $ {v}_{2}=\dfrac{5ℎ}{t} $ ,根据自由落体公式有 $ ℎ=\dfrac{1}{2}g{t}^{2} $ ,联立可得 $ {v}_{1}=g\cdot \dfrac{1}{2}t $ , $ {v}_{2}=g\cdot \dfrac{5}{2}t $ ,可知小石子通过 $ OB $ 段所用的时间为 $ {t}_{OB}=\dfrac{{v}_{2}}{g}-\dfrac{t}{2}=2t $ , $ OB $ 段的高度为 $ H=\dfrac{1}{2}g(2t)^{2}=4ℎ $ ,故 $ OB $ 段共4层,该楼房共9层, $ \mathrm{B} $ 正确, $ \mathrm{A} $ 、 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
4.某同学用“滴水法”研究水珠的自由落体运动,稍扭松水龙头,待稳定后确保每隔相同时间总有一滴水珠从水龙头出水口处落下.通过观察发现,相邻水珠落下时刻的时间间隔为 $ T $ .现从某一水珠刚落下时刻开始计时,且将该水珠计数为1,当第5滴水珠刚从出水口落下时,第1滴水珠恰好落到地面上.水龙头出水口到地面的高度为 $ H $ ,重力加速度为 $ g $ ,则( )
A. $ H=4g{T}^{2} $
B. $ H=3g{T}^{2} $
C. $ H=8g{T}^{2} $
D. $ H=18g{T}^{2} $
答案:C
解析:由题意可知,当第5滴水珠刚从出水口落下时,第1滴水珠恰好落到地面上,则第1滴水珠与第5滴水珠间的时间间隔为 $ t=4T $ ,由自由落体运动公式可得,水龙头出水口到地面的高度为 $ H=\dfrac{1}{2}g{t}^{2}=\dfrac{1}{2}g(4T)^{2}=8g{T}^{2} $ ,故选 $ \mathrm{C} $ .
5.鸡蛋从高处落到地面而不被摔坏,撞击地面的速度最大不能超过 $ 1\mathrm{m}/\mathrm{s} $ .某同学设计了如图所示的保护装置,用 $ A $ 、 $ B $ 两块较粗糙的夹板夹住鸡蛋,现让该装置从距地面某一高处自由下落,装置着地后速度立即减为零,且保持竖直,此后鸡蛋在 $ A $ 、 $ B $ 夹板间减速下落的加速度大小为 $ 9g $ .(不计空气阻力, $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ )

(1) 如果没有保护,求鸡蛋自由下落而不被摔坏时释放的最大高度 $ ℎ $ ;
(2) 某次试验中保护装置从离地面 $ H=5\mathrm{m} $ 的高度处静止释放,为保证鸡蛋安全,求鸡蛋放的位置离装置下端的最小距离 $ s $ ;
(3) 求在满足第(2)问情况下鸡蛋运动的总时间 $ t $ .
答案:(1) $ 0.05\mathrm{m} $
(2) $ 0.55\mathrm{m} $
(3) $ 1.1\mathrm{s} $
解析:(1) 由题意知,鸡蛋做自由落体运动,由自由落体运动的规律得 $ {v}^{2}=2gℎ $ ,解得 $ ℎ=0.05\mathrm{m} $ .
(2) 保护装置和鸡蛋共同自由下落,有 $ {v}_{1}^{2}=2gH $ ,保护装置着地后鸡蛋开始减速,所以为保证鸡蛋安全,到达地面时速度不超过 $ v=1\mathrm{m}/\mathrm{s} $ ,鸡蛋放的位置到装置下端的最小距离 $ s $ 满足 $ {v}_{1}^{2}-{v}^{2}=2as $ ,代入数据联立解得 $ s=0.55\mathrm{m} $ .
(3) 鸡蛋和保护装置自由下落时有 $ H=\dfrac{1}{2}g{t}_{1}^{2} $ ,减速时有 $ v={v}_{1}-a{t}_{2} $ ,鸡蛋运动的总时间 $ t={t}_{1}+{t}_{2} $ ,联立解得 $ t=1.1\mathrm{s} $ .
6.一根竖直杆 $ AB $ ,在其下端 $ B $ 以下 $ 20\mathrm{c}\mathrm{m} $ 处固定一长度为 $ 1\mathrm{m} $ 的竖直管(杆能穿过管),杆自由下落,穿过竖直管所用时间为 $ 0.4\mathrm{s} $ (穿过的过程是指从两个物体刚刚有重叠到完全没有重叠的过程,且杆与管间无相互作用), $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则竖直杆 $ AB $ 的长度为( )
A. $ 0.2\mathrm{m} $
B. $ 0.4\mathrm{m} $
C. $ 0.6\mathrm{m} $
D. $ 0.8\mathrm{m} $
答案:C
解析:杆做自由落体运动,杆的下端 $ B $ 由静止下落到管口的过程有 $ ℎ=\dfrac{1}{2}g{t}_{1}^{2} $ ,设杆 $ AB $ 的长度为 $ L $ ,竖直管长度为 $ l=1\mathrm{m} $ ,杆的上端 $ A $ 下落到管底端的过程有 $ ℎ+L+l=\dfrac{1}{2}g{t}_{2}^{2} $ ,穿过管所用的时间 $ \mathrm{\Delta }t={t}_{2}-{t}_{1} $ ,联立解得 $ L=0.6\mathrm{m} $ ,故 $ \mathrm{C} $ 正确.
7.小兰设计了不同的实验方案测量当地重力加速度.
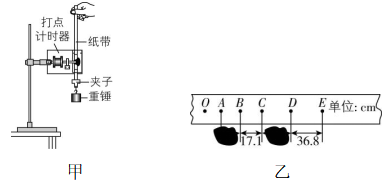
(1) ① 如图甲,下列实验步骤的正确顺序是 .
A.断开电源,取下纸带,计算重力加速度
B.接通电源,使电火花计时器开始工作
C.释放重锤,带动纸带做自由落体运动
② 能使电火花计时器正常工作的电源是 .
A. $ 220\mathrm{V} $ , $ 50\mathrm{H}\mathrm{z} $ 交流电
B. $ 4\sim 6\mathrm{V} $ , $ 50\mathrm{H}\mathrm{z} $ 交流电
C.两节干电池
③ 图乙中标出的相邻两计数点之间还有4个计时点未画出,纸带部分被污染,则根据现有数据计算出重力加速度为 $ \mathrm{m}/{\mathrm{s}}^{2} $ .(保留三位有效数字)
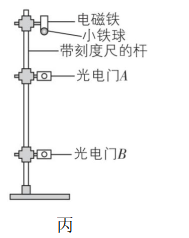
(2) ①如图丙,两个光电门间隔为 $ L $ ,小球直径为 $ d $ ,将小球静止释放后依次通过两个光电门,时间依次为 $ {t}_{1} $ , $ {t}_{2} $ ,则用所给字母表示重力加速度 $ g= $ .
②如果释放时具有向下的初速度,测得的重力加速度将 (填“偏大”“偏小”或“不变”).
答案:① BCA
② A
③ 9.85
(2) $ \dfrac{{d}^{2}}{2L}(\dfrac{1}{{t}_{2}^{2}}-\dfrac{1}{{t}_{1}^{2}}) $ ;不变
解析:① 实验步骤为:先接通电源,使打点计时器工作后再释放重锤,使其拖动纸带打点,然后关闭电源,取下纸带,进行数据分析,故正确的顺序为BCA.
② 电火花计时器使用“ $ 220\mathrm{V} $ , $ 50\mathrm{H}\mathrm{z} $ ”的交流电作为工作电源,故选A.
③ 根据逐差法求加速度可得 $ {x}_{DE}-{x}_{BC}=2g{T}^{2} $ ,解得 $ g=\dfrac{{x}_{DE}-{x}_{BC}}{2{T}^{2}}=\dfrac{(36.8-17.1)×{10}^{-2}}{2×{0.1}^{2}}\mathrm{m}/{\mathrm{s}}^{2}=9.85\mathrm{m}/{\mathrm{s}}^{2} $ .
(2) ①小球通过两光电门的速度分别为 $ {v}_{1}=\dfrac{d}{{t}_{1}} $ 、 $ {v}_{2}=\dfrac{d}{{t}_{2}} $ ,故重力加速度 $ g=\dfrac{{v}_{2}^{2}-{v}_{1}^{2}}{2L}=\dfrac{{d}^{2}}{2L}(\dfrac{1}{{t}_{2}^{2}}-\dfrac{1}{{t}_{1}^{2}}).\mathrm{②} $ 小球释放时具有向下的初速度,对利用光电门计算的速度没有影响,故测量的重力加速度的值不变.
8.如图所示,从高出地面 $ 3\mathrm{m} $ 的位置竖直向上抛出一个小球,它上升 $ 5\mathrm{m} $ 后回落,最后到达地面,以抛出点为原点建立一维坐标系,方向以向上为正,不计空气阻力, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法正确的是( )
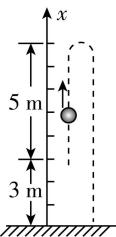
A.整个过程中,小球的路程为 $ 8\mathrm{m} $
B.小球初速度为 $ 10\mathrm{m}/\mathrm{s} $
C.从抛出点到落地点小球的位移为 $ -8\mathrm{m} $
D.上升过程和下降过程中加速度大小相等,方向相反
答案:B
解析:整个过程中,小球的路程为 $ s=5\mathrm{m}+5\mathrm{m}+3\mathrm{m}=13\mathrm{m} $ ,故 $ \mathrm{A} $ 错误;根据 $ 0-{v}_{0}^{2}=-2gℎ $ ,解得小球初速度为 $ {v}_{0}=\sqrt{2gℎ}=\sqrt{2×10×5}\mathrm{m}/\mathrm{s}=10\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{B} $ 正确;从抛出点到落地点小球的位移为 $ x=-3\mathrm{m} $ ,故 $ \mathrm{C} $ 错误;上升过程和下降过程中加速度均为重力加速度,大小相等,方向相同,故 $ \mathrm{D} $ 错误.
9.如图所示,小球甲从距离地面高度为 $ {ℎ}_{1}=15\mathrm{m} $ 处以速度 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ 竖直向上抛出,同时小球乙从距离地面高度为 $ {ℎ}_{2}=20\mathrm{m} $ 处开始自由下落,小球运动的过程中不计空气阻力,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法中正确的是( )
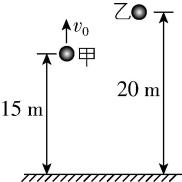
A.小球乙落地前,两小球的速度差逐渐变大
B.落地前的运动过程中小球甲、乙的平均速率之比为 $ 5:6 $
C.至小球乙落地时,甲、乙两球的位移大小之比为 $ 3:4 $
D.小球甲、乙运动的第 $ 1\mathrm{s} $ 内位移相同
答案:B
解析:以小球乙为参考系,小球甲向上做匀速直线运动,小球乙落地前,两小球的速度差值不变,等于 $ 10\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 错误;小球甲、乙运动的第 $ 1\mathrm{s} $ 内位移大小分别为 $ {ℎ}_{甲1}=10×1\mathrm{m}-\dfrac{1}{2}×10×{1}^{2}\mathrm{m}=5\mathrm{m} $ 、 $ {ℎ}_{乙1}=\dfrac{1}{2}×10×{1}^{2}\mathrm{m}=5\mathrm{m} $ ,两个小球的位移大小相等,方向相反,位移不相同, $ \mathrm{D} $ 错误;小球乙落地时间为 $ t=\sqrt{\dfrac{2{ℎ}_{2}}{g}}=2\mathrm{s} $ ,小球乙落地时,甲、乙两球的位移大小分别为 $ {ℎ}_{甲}={v}_{0}t-\dfrac{1}{2}g{t}^{2}=0 $ 、 $ {ℎ}_{乙}=20\mathrm{m} $ , $ \mathrm{C} $ 错误;乙球经过 $ t=2\mathrm{s} $ 落地,乙球的平均速率为 $ {\overline{v}}_{乙}=\dfrac{20}{2}\mathrm{m}/\mathrm{s}=10\mathrm{m}/\mathrm{s} $ ,甲球上升到最高点所用时间为 $ {t}_{上}=\dfrac{{v}_{0}}{g}=1\mathrm{s} $ , $ 1\mathrm{s} $ 内上升的高度为 $ {ℎ}_{1}=\dfrac{1}{2}g{t}_{上}^{2}=5\mathrm{m} $ ,离地面的最大高度为 $ 20\mathrm{m} $ ,自由落体的时间也是 $ 2\mathrm{s} $ ,则甲球的平均速率为 $ {\overline{v}}_{甲}=\dfrac{5+5+15}{3}\mathrm{m}/\mathrm{s}=\dfrac{25}{3}\mathrm{m}/\mathrm{s} $ ,甲、乙两球的平均速率之比为 $ \dfrac{{\overline{v}}_{甲}}{{\overline{v}}_{乙}}=\dfrac{5}{6} $ , $ \mathrm{B} $ 正确.
10.如图所示,我国自主研发的“极目一号”Ⅲ型浮空艇创造了海拔 $ 9032\mathrm{m} $ 的大气科学观测世界纪录.若某段过程中,浮空艇以 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ 的速度匀速上升,当到达离地面高 $ ℎ=175\mathrm{m} $ 处时,从浮空艇上掉下一个重物(不计空气阻力,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ).

(1) 重物经多长时间落到地面?
(2) 重物从浮空艇上掉落到落地过程中运动的路程是多少?
答案:(1) $ 7\mathrm{s} $
(2) $ 185\mathrm{m} $
解析:(1) 重物掉落后以 $ {v}_{0} $ 向上做匀减速运动,上升到最高点时速度减到零,故其上升的时间和上升的高度分别为 $ {t}_{1}=\dfrac{{v}_{0}}{g}=1\mathrm{s} $ 、 $ {ℎ}_{1}=\dfrac{{v}_{0}^{2}}{2g}=5\mathrm{m} $ ,故重物将上升到离地面高度为 $ H=ℎ+{ℎ}_{1}=180\mathrm{m} $ 处,重物从最高处开始做自由落体运动,根据自由落体运动的规律有 $ H=\dfrac{1}{2}g{t}_{2}^{2} $ ,解得重物自由落体时间为 $ {t}_{2}=\sqrt{\dfrac{2H}{g}}=6\mathrm{s} $ ,
重物落地共需时间为 $ t={t}_{1}+{t}_{2}=7\mathrm{s} $ .
(2) 重物从掉落到落地运动的路程为 $ s=H+{ℎ}_{1}=185\mathrm{m} $ .
二、刷提升
1.假设运动员从 $ 10\mathrm{m} $ 跳台起跳后沿一条直线运动,起跳时其重心比跳台台面高 $ 1.0\mathrm{m} $ ,运动员到达最高位置时,其重心比跳台台面高 $ 1.8\mathrm{m} $ ,运动员下降到手触及水面时,其重心比水面高 $ 1.0\mathrm{m} $ .将运动员视为质点,不计空气阻力,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法正确的是( )

A.运动员的起跳速度大小为 $ 5\mathrm{m}/\mathrm{s} $
B.运动员从起跳到手刚触及水面的时间为 $ \dfrac{2+3\sqrt{6}}{5}\mathrm{s} $
C.运动员的位移大小为 $ 0.6\mathrm{m} $ 时,对应两个时刻
D.运动员的手刚触及水面时的速度大小为 $ (8+10\sqrt{2})\mathrm{m}/\mathrm{s} $
答案:B
解析:由题意知运动员从起跳到上升到最高点,重心上升了 $ {ℎ}_{1}=1.8\mathrm{m}-1.0\mathrm{m}=0.8\mathrm{m} $ ,运动员的起跳速度大小为 $ {v}_{0}=\sqrt{2g{ℎ}_{1}}=4\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{A} $ 错误;运动员从起跳到上升到最高点的时间为 $ {t}_{1}=\sqrt{\dfrac{2{ℎ}_{1}}{g}}=0.4\mathrm{s} $ ,由题意可知运动员从最高点到手刚触及水面重心下降了 $ {ℎ}_{2}=1.8\mathrm{m}+(10-1.0)\mathrm{m}=10.8\mathrm{m} $ ,下落时间 $ {t}_{2}=\sqrt{\dfrac{2{ℎ}_{2}}{g}}=\dfrac{3\sqrt{6}}{5}\mathrm{s} $ ,运动员的手刚触及水面时的速度大小为 $ {v}_{2}=\sqrt{2g{ℎ}_{2}}=6\sqrt{6}\mathrm{m}/\mathrm{s} $ ,运动员从起跳到手刚触及水面的时间为 $ t={t}_{1}+{t}_{2}=\dfrac{2+3\sqrt{6}}{5}\mathrm{s} $ ,故 $ \mathrm{B} $ 正确, $ \mathrm{D} $ 错误;当运动员的位移大小为 $ 0.6\mathrm{m} $ 时,可以在跳台上方,对应两个时刻,也可以在跳台下方,对应一个时刻,所以运动员的位移大小为 $ 0.6\mathrm{m} $ 时,对应三个时刻,故 $ \mathrm{C} $ 错误.
2.测 $ g $ 值的一种方法叫“对称自由下落法”.具体做法:将真空长直管沿竖直方向放置,自其中 $ O $ 点竖直向上抛出小球,小球又落回原处的时间为 $ {T}_{1} $ ,在小球运动过程中经过比 $ O $ 点高 $ ℎ $ 的 $ P $ 点,小球离开 $ P $ 点至又回到 $ P $ 点所用的时间为 $ {T}_{2} $ ,测得 $ {T}_{1} $ 、 $ {T}_{2} $ 和 $ ℎ $ ,可求得 $ g $ 等于( )
A. $ \dfrac{4ℎ}{{T}_{1}^{2}-{T}_{2}^{2}} $
B. $ \dfrac{ℎ}{4({T}_{1}-{T}_{2})^{2}} $
C. $ \dfrac{8ℎ}{{T}_{1}^{2}-{T}_{2}^{2}} $
D. $ \dfrac{ℎ}{8({T}_{1}-{T}_{2})^{2}} $
答案:C
解析:根据位移—时间关系可得 $ ℎ=\dfrac{1}{2}g{\left(\dfrac{{T}_{1}}{2}\right) ^ {2}}-{\dfrac{1}{2}g(\dfrac{{T}_{2}}{2})}^{2} $ ,联立解得 $ g=\dfrac{8ℎ}{{T}_{1}^{2}-{T}_{2}^{2}} $ ,故选 $ \mathrm{C} $ .
3.“笛音雷”是一种鞭炮,其点燃后一段时间内的速度—时间图像如图所示(不计空气阻力,取竖直向上为正方向),其中 $ {t}_{0} $ 时刻为“笛音雷”起飞时刻, $ DE $ 段是斜率的绝对值等于重力加速度 $ g $ 的直线.下列说法正确的是( )
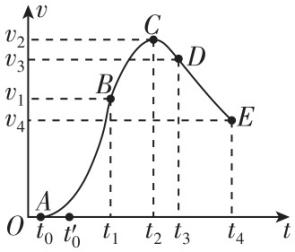
A.“笛音雷”在 $ {t}_{2} $ 时刻上升至最高点
B. $ {t}_{3}\sim {t}_{4} $ 时间内,“笛音雷”做自由落体运动
C. $ {t}_{0}\sim {t}_{2} $ 时间内,“笛音雷”的平均速度接近 $ \dfrac{{v}_{2}}{2} $
D.若另一颗“笛音雷”在 $ t{\prime }_{0} $ 时刻起飞,其后的运动情况与在 $ {t}_{0} $ 时刻起飞的“笛音雷”一样,则二者间的距离先越来越小,后越来越大
答案:C
解析:取竖直向上为正方向,由题图可知, $ {t}_{0}\mathrm{~}{t}_{4} $ 时间内“笛音雷”的速度方向始终向上,在 $ {t}_{2} $ 时刻速度达到最大,故“笛音雷”在 $ {t}_{2} $ 时刻没有上升至最高点,故 $ \mathrm{A} $ 错误;根据 $ v-t $ 图像切线的斜率表示加速度可知, $ {t}_{3}\sim {t}_{4} $ 时间内“笛音雷”的加速度为重力加速度,速度方向竖直向上,故“笛音雷”做竖直上抛运动,故 $ \mathrm{B} $ 错误; $ v-t $ 图像与横轴围成的图形面积表示位移,将 $ A $ 、 $ C $ 两点连接起来,线段 $ AC $ 表示做匀加速直线运动,其平均速度为 $ \overline{v}=\dfrac{0+{v}_{2}}{2}=\dfrac{{v}_{2}}{2} $ ,由题图可知 $ {t}_{0}\sim {t}_{2} $ 时间内线段 $ AC $ 与横轴围成的图形面积与曲线 $ ABC $ 与横轴围成的图形面积大小接近,即位移接近,运动时间相同,故 $ {t}_{0}\sim {t}_{2} $ 时间内“笛音雷”的平均速度接近 $ \dfrac{{v}_{2}}{2} $ ,故 $ \mathrm{C} $ 正确;将题图中实线向右平移至过 $ t=t{\prime }_{0} $ ,即得到 $ t{\prime }_{0} $ 时刻起飞的“笛音雷”的 $ v-t $ 图像,可知两颗“笛音雷”间的距离先越来越大,在两图线交点处距离最大,然后两者间的距离越来越小,故 $ \mathrm{D} $ 错误.
4.一个探险队登上一座小山峰,山峰一侧是悬崖,探险队一个队员向悬崖下丢了一块石头,放手时石头的初速度为零,丢下石头的同时开始计时, $ 10\mathrm{s} $ 时听到石头落地的响声,声音在空气中传播的速度为 $ 340\mathrm{m}/\mathrm{s} $ ,重力加速度大小取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,空气阻力忽略不计,则( )(多选)
A.悬崖的高度一定小于 $ 405\mathrm{m} $
B.悬崖的高度可能小于 $ 320\mathrm{m} $
C.石头落地的速度一定大于 $ 80\mathrm{m}/\mathrm{s} $
D.石头在第 $ 9\mathrm{s} $ 内的位移为 $ 85\mathrm{m} $
答案:AC
解析:设悬崖的高度为 $ ℎ $ ,根据题意可得 $ t=\sqrt{\dfrac{2ℎ}{g}}+\dfrac{ℎ}{{v}_{声}} $ ,整理得 $ t=\sqrt{\dfrac{ℎ}{5}}+\dfrac{ℎ}{340}(\mathrm{s}) $ ,若 $ ℎ=405\mathrm{m} $ ,则 $ t=(\sqrt{\dfrac{405}{5}}+\dfrac{405}{340})\mathrm{s}=(9+\dfrac{405}{340})\mathrm{s} > 10\mathrm{s} $ ,故悬崖的高度一定小于 $ 405\mathrm{m} $ ,故 $ \mathrm{A} $ 正确;若 $ ℎ=320\mathrm{m} $ ,则 $ t=(\sqrt{\dfrac{320}{5}}+\dfrac{320}{340})\mathrm{s}=(8+\dfrac{320}{340})\mathrm{s} < 10\mathrm{s} $ ,故悬崖的高度一定大于 $ 320\mathrm{m} $ ,故 $ \mathrm{B} $ 错误;因悬崖的高度一定大于 $ 320\mathrm{m} $ ,石头落地的速度 $ v=\sqrt{2gℎ} > \sqrt{2×10×320}\mathrm{m}/\mathrm{s}=80\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 正确;若石头下落时间不小于 $ 9\mathrm{s} $ ,则石头在第 $ 9\mathrm{s} $ 内下落的高度为 $ {ℎ}_{9}=\dfrac{1}{2}g{t}_{9}^{2}-\dfrac{1}{2}g{t}_{8}^{2}=(\dfrac{1}{2}×10×{9}^{2}-\dfrac{1}{2}×10×{8}^{2})\mathrm{m}=85\mathrm{m} $ ,由前面分析可知,石头下落的时间 $ 8\mathrm{s} < t < 9\mathrm{s} $ ,故石头在第 $ 9\mathrm{s} $ 内的位移小于 $ 85\mathrm{m} $ ,故 $ \mathrm{D} $ 错误.
5.如图所示,离地面足够高处有一竖直的空管,管长为 $ 24\mathrm{m} $ , $ M $ 、 $ N $ 为空管的上、下两端,空管受外力作用,由静止开始竖直向下做匀加速直线运动,加速度大小为 $ 2\mathrm{m}/{\mathrm{s}}^{2} $ .同时在 $ M $ 处将一个大小不计的小球沿管的轴线以初速度 $ {v}_{0} $ 竖直上抛,不计一切阻力,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .
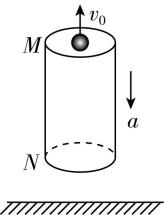
(1) 若小球上抛的初速度为 $ 10\mathrm{m}/\mathrm{s} $ ,从抛出开始计时,经过多长时间从管的 $ N $ 端穿出?
(2) 若此空管的 $ N $ 端距离地面 $ 64\mathrm{m} $ 高,欲使在空管到达地面时小球必须落到管内且不反弹,在其他条件不变的前提下,求小球的初速度 $ {v}_{0} $ 大小的范围.
答案:(1) $ 4\mathrm{s} $
(2) $ 29\mathrm{m}/\mathrm{s}⩽ {v}_{0}⩽ 32\mathrm{m}/\mathrm{s} $
解析:(1) 取竖直向下为正方向,设经 $ t $ 时间,小球从 $ N $ 端穿出,小球下落的高度 $ {ℎ}_{1}=-{v}_{0}t+\dfrac{1}{2}g{t}^{2} $ ,
空管下落的高度 $ {ℎ}_{2}=\dfrac{1}{2}a{t}^{2} $ ,
又 $ {ℎ}_{1}-{ℎ}_{2}=L $ ,
代入数据联立解得 $ t=4\mathrm{s} $ .
(2) 设空管经 $ t\prime $ 时间到达地面,则有 $ H=\dfrac{1}{2}at{\prime }^{2} $ ,
解得 $ t\prime =\sqrt{\dfrac{2H}{a}}=8\mathrm{s} $ ,
小球在 $ t\prime $ 时间内下落高度为 $ ℎ=-{v}_{0}t\prime +\dfrac{1}{2}gt{\prime }^{2} $ ,
小球落入管内的条件是 $ 64\mathrm{m}⩽ ℎ⩽ (64+24)\mathrm{m} $ ,
解得 $ 29\mathrm{m}/\mathrm{s}⩽ {v}_{0}⩽ 32\mathrm{m}/\mathrm{s} $ ,
所以小球的初速度大小必须在 $ 29\mathrm{m}/\mathrm{s}⩽ {v}_{0}⩽ 32\mathrm{m}/\mathrm{s} $ 范围内.
![]()








