1.两个实验小组分别采用了不同的装置来测定物体的加速度.第一小组利用了电磁打点计时器和纸带,如图1所示,第二小组使用了气垫导轨和光电门,如图2所示.
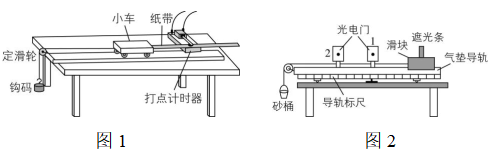
(1) 关于电磁打点计时器,以下说法正确的是 (多选);
A.采用直流电源供电,电压为 $ 220\mathrm{V} $
B.打点的周期由交流电的频率决定
C.纸带移动速度越大,相邻两点的间距越大
D.纸带移动速度越小,相邻两点的间距越大
(2) 关于光电门测速度,下列说法正确的是 (多选);
A.利用光电门测量的速度可以近似认为是瞬时速度
B.图2中滑块通过光电门1的时间小于通过光电门2的时间
C.遮光条宽度适当窄一些,光电门测量的瞬时速度更准确
D.利用光电门只能测量物体做匀变速直线运动的速度
(3) 第一小组得到纸带的一部分如图3所示,图中 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 、 $ E $ 为相邻的计数点,每两个相邻计数点间有4个计时点(未画出),分别测出 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 、 $ E $ 相邻两点之间的距离为 $ {x}_{1} $ 、 $ {x}_{2} $ 、 $ {x}_{3} $ 、 $ {x}_{4} $ ,已知打点计时器所接电源频率为 $ f $ ,则小车运动的加速度 $ a= $ (用 $ {x}_{1} $ 、 $ {x}_{2} $ 、 $ {x}_{3} $ 、 $ {x}_{4} $ 、 $ f $ 表示);
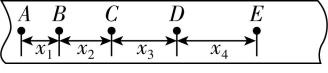
图3
(4) 第二小组实验中,由导轨标尺可以测出两个光电门之间的距离为 $ L $ ,遮光条固定在滑块上,用数字计时器测得遮光条通过两个光电门的遮光时间分别为 $ {t}_{1} $ 和 $ {t}_{2} $ ,已知遮光条的宽度为 $ d $ ,则滑块运动的加速度 $ a= $ (用 $ L $ 、 $ {t}_{1} $ 、 $ {t}_{2} $ 、 $ d $ 表示).
答案:(1) BC
(2) AC
(3) $ \dfrac{({x}_{4}+{x}_{3}-{x}_{2}-{x}_{1}){f}^{2}}{100} $
(4) $ \dfrac{{d}^{2}}{2L}(\dfrac{1}{{t}_{2}^{2}}-\dfrac{1}{{t}_{1}^{2}}) $
解析:(1) 电磁打点计时器采用交流电源供电,电压为 $ 8\mathrm{V} $ 左右, $ \mathrm{A} $ 错误;打点的周期由交流电的频率决定, $ \mathrm{B} $ 正确;因打点周期一定,则纸带移动速度越大,相邻两点的间距越大, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
(2) 因遮光条遮光时间很短,则平均速度可近似认为等于瞬时速度,即利用光电门测量的速度可以近似认为是瞬时速度, $ \mathrm{A} $ 正确;滑块做加速运动,则题图2中滑块通过光电门1的时间大于通过光电门2的时间, $ \mathrm{B} $ 错误;遮光条宽度适当窄一些,平均速度更接近瞬时速度,即光电门测量的瞬时速度更准确, $ \mathrm{C} $ 正确;利用光电门能测量物体做任何直线运动的瞬时速度, $ \mathrm{D} $ 错误.
(3) 每两个相邻计数点间有4个计时点未画出,可得 $ T=\dfrac{5}{f} $ ,则小车运动的加速度 $ a=\dfrac{{x}_{4}+{x}_{3}-{x}_{2}-{x}_{1}}{4{T}^{2}}=\dfrac{({x}_{4}+{x}_{3}-{x}_{2}-{x}_{1}){f}^{2}}{100} $ .
(4) 遮光条通过两个光电门的速度分别为 $ {v}_{1}=\dfrac{d}{{t}_{1}} $ 、 $ {v}_{2}=\dfrac{d}{{t}_{2}} $ ,加速度 $ a=\dfrac{{v}_{2}^{2}-{v}_{1}^{2}}{2L}=\dfrac{{d}^{2}}{2L}(\dfrac{1}{{t}_{2}^{2}}-\dfrac{1}{{t}_{1}^{2}}) $ .
2.某同学用如图(a)所示的实验装置研究匀变速运动,将木块从倾角为 $ \theta $ 的木板上静止释放,与位移传感器连接的计算机描绘出了木块相对传感器的位置随时间变化的规律,如图(b)中的曲线②所示.图中木块的位置从 $ {x}_{1} $ 到 $ {x}_{2} $ 、从 $ {x}_{2} $ 到 $ {x}_{3} $ 的运动时间均为 $ T $ .

(1) 根据图(b)可得,木块经过位置 $ {x}_{2} $ 时的速度 $ {v}_{2}= $ ,木块运动的加速度 $ a= $ (用已给物理量的字母表示).
(2) 若只增大木板的倾角,则木块相对传感器的位置随时间变化的规律可能是图(b)中的曲线 .
答案:(1) $ \dfrac{{x}_{3}-{x}_{1}}{2T} $ ; $ \dfrac{{x}_{3}-2{x}_{2}+{x}_{1}}{{T}^{2}} $
(2) ①
解析:(1) 木块在木板上做匀加速直线运动,则木块经过位置 $ {x}_{2} $ 时的速度 $ {v}_{2}=\dfrac{{x}_{3}-{x}_{1}}{2T} $ ,相邻相等时间内位移之差 $ \mathrm{\Delta }x=a{T}^{2} $ ,故 $ {x}_{3}-2{x}_{2}+{x}_{1}=a{T}^{2} $ ,解得 $ a=\dfrac{{x}_{3}-2{x}_{2}+{x}_{1}}{{T}^{2}} $ .
(2) 若只增大木板的倾角,则木块的加速度增大,根据 $ x=\dfrac{1}{2}a{t}^{2} $ 可知木块相对传感器的位移随时间变化的规律可能是题图(b)中的①.
3.实验小组利用图1所示的装置探究“物块速度与高度的关系”.主要探究思路如下:
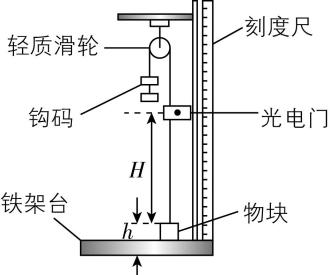
图1
①安装完装置,测量方形小物块的高度 $ ℎ $ 及其上沿距光电门中心的高度 $ H $ ;
②悬挂一定数量的钩码,将物块从铁架台底部由静止释放,记录物块通过光电门的遮光时间 $ t $ ;
③改变光电门的高度,测量物块上沿距光电门中心的高度,重复第②步……由此可得到多组数据 $ (H,t) $ ;
④整理器材,完成数据探究.
(1) 关于该实验,下列说法正确的是 (单选,填正确答案标号).
A.每次静止释放钩码前,应确保细线均处于竖直状态
B.每次操作时,钩码数量可随意增减
(2) 速度计算:若小组中某同学将物块通过光电门时遮光的平均速度当作其上沿到达光电门中心的瞬时速度,则该同学得到的物块上沿到达光电门中心的速度表达式 $ v= $ (用题给物理量符号表示).
(3) 规律探究:该同学描绘出了 $ H-t $ 关系图像,如图2所示.为便于探究,请帮助分析:纵轴仍为 $ H $ 、横轴应改为 (单选,填正确答案标号)才能得到图3所示的线性关系.

A. $ \dfrac{1}{t} $ B. $ \dfrac{1}{{t}^{2}} $ C. $ {t}^{2} $
(4) 误差分析:该同学通过帮助得到如图3所示的线性(正比)关系图像,计算得到该直线的斜率为 $ k $ .考虑到物块上沿到达光电门中心的瞬时速度与遮光的平均速度的差异,则实验得到的图线斜率 $ k $ 比理论上的斜率 (填“偏大”或“偏小”).
答案:(1) A
(2) $ \dfrac{ℎ}{t} $
(3) B
(4) 偏小
解析:(1) 每次静止释放钩码前,应确保细线均处于竖直状态,保证物块在竖直方向做直线运动,故 $ \mathrm{A} $ 正确;每次操作时,钩码数量应保持不变,故 $ \mathrm{B} $ 错误.
(2) 物块上沿到达光电门中心的速度表达式 $ v=\dfrac{ℎ}{t} $ .
(3) 设物块和钩码的加速度大小为 $ a $ ,由 $ {v}^{2}=2aH $ ,得 $ {\left(\dfrac{ℎ}{t}\right) ^ {2}}=2aH $ , $ H=\dfrac{{ℎ}^{2}}{2a}\cdot \dfrac{1}{{t}^{2}} $ ,则纵轴仍为 $ H $ 、横轴应改为 $ \dfrac{1}{{t}^{2}} $ 才能得到题图3所示的线性关系.故选 $ \mathrm{B} $ .
(4) 物块上沿到达光电门中心的瞬时速度小于遮光的平均速度,故实验得到的图线斜率 $ k $ 比理论上的斜率偏小.
4.自由落体运动速度很快,在当时的技术条件下,很难精确测量物体下落的时间等数据,于是伽利略想到通过减小物体下落的加速度来延长运动时间,以便更准确地进行研究,由此设计了斜面实验.
(1) 伽利略将落体实验转化为著名的“斜面实验”,从而创造了一种科学研究的方法.利用斜面实验主要是考虑到 .
A.实验时能更准确地测量小球运动的速度、加速度和路程
B.实验时便于测量小球运动的时间和加速度
C.实验时便于测量小球运动的路程和位移
D.斜面实验可以直接得出落体的运动规律
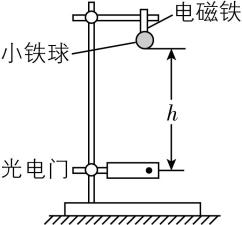
(2) 某校物理学习小组的同学们设计了如图甲所示的实验装置来更精确地测量重力加速度的大小.
甲
该小组采用了以下实验步骤:铁球一开始被通电的电磁铁吸住,电磁铁断电即释放铁球.铁球下落途中会经过一光电门,光电门发射端与接收端在同一高度,且铁球经过光电门时,光电门可以记录它的遮光时间 $ t $ ,光电门的安装位置可以上下调整,从而改变释放时铁球下端到光电门发射端的竖直高度 $ ℎ $ ,另外测得实验时所用铁球的直径为 $ d $ .
① 上述实验中铁球通过光电门的速度 $ v= $ (用题中所测物理量字母表示);
② 保持电磁铁的位置不变,多次改变光电门的位置,重复实验,测得多组 $ ℎ $ 、 $ t $ 的值,作 $ ℎ-\dfrac{1}{{t}^{2}} $ 图像(铁球半径不能忽略),则作出的图像应是图乙中的图线 (填“ $ a $ ”“ $ b $ ”或“ $ c $ ”),其中所选图线的斜率 $ k= $ (用 $ d $ 和 $ g $ 表示);
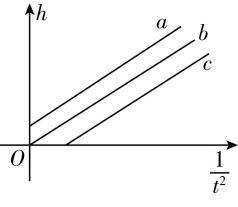
乙
③ 若铁球直径 $ d $ 的测量值比铁球实际直径偏小,则实验中所测得的重力加速度 $ g $ 的大小与真实结果相比 (填“偏大”“相等”或“偏小”).
答案:(1) B
(2) ① $ \dfrac{d}{t} $
② $ c $ ; $ \dfrac{{d}^{2}}{2g} $
③ 偏小
解析:(1) 斜面实验主要考虑到实验时便于测量小球运动的时间和通过研究得出加速度.故选 $ \mathrm{B} $ .
(2) ① 根据极短时间的平均速度等于瞬时速度,可知铁球通过光电门的速度为 $ v=\dfrac{d}{t}. $
② 根据运动学公式有 $ ℎ+\dfrac{d}{2}=\dfrac{{v}^{2}}{2g} $ ,整理得 $ ℎ=\dfrac{{d}^{2}}{2g}\cdot \dfrac{1}{{t}^{2}}-\dfrac{d}{2} $ ,可知 $ ℎ-\dfrac{1}{{t}^{2}} $ 图像的纵截距小于零,故作出的图像应为题图乙中的图线 $ c $ .若图线的斜率为 $ k $ ,则 $ k=\dfrac{{d}^{2}}{2g}. $
③ 根据上述结果可知 $ g=\dfrac{{d}^{2}}{2k} $ ,若直径 $ d $ 测量值偏小,则所测得的 $ g $ 值比真实结果偏小.






