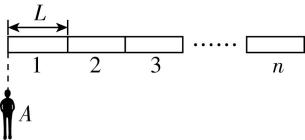
13.(14分)如图所示,在离地面高 $ H $ 处以 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ 的速度竖直向上抛出一个可视为质点的小球,地面上有一长 $ L=6\mathrm{m} $ 的小车,其前端 $ M $ 与抛出点所在竖直线之间距离为 $ s=3\mathrm{m} $ ,小球抛出的同时,小车由静止开始向右做 $ {a}_{1}=2\mathrm{m}/{\mathrm{s}}^{2} $ 的匀加速直线运动.已知小球落地前最后 $ 1\mathrm{s} $ 内下落的高度为 $ 25\mathrm{m} $ ,忽略空气阻力及小车的高度,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .
(2) 当小车末端 $ N $ 到达抛出点正下方时,便立即做加速度大小恒为 $ {a}_{2} $ 、方向与此时速度方向相反的匀变速直线运动,为了让小车接住小球,试确定 $ {a}_{2} $ 的取值范围.
解析:(1) 设小球从最高点下落至地面所用的时间为 $ {t}_{1} $ ,最大高度为 $ ℎ $ ,由运动学公式有
$ ℎ=\dfrac{1}{2}g{t}_{1}^{2} $ , $ ℎ-25\mathrm{m}=\dfrac{1}{2}g({t}_{1}-1\mathrm{s})^{2} $ ,
解得 $ {t}_{1}=3\mathrm{s} $ , $ ℎ=45\mathrm{m} $ ,
小球从抛出到到达最高点的时间为 $ {t}_{0}=\dfrac{{v}_{0}}{g}=1\mathrm{s} $ ,
故小球从抛出到下落到地面所用的时间 $ t={t}_{1}+{t}_{0}=4\mathrm{s} $ ,
选抛出点为初始位置,落地点为末位置,规定向下为正方向,由 $ x={v}_{0}t+\dfrac{1}{2}a{t}^{2} $ 可得,抛出点离地面的高度 $ H=-10×4\mathrm{m}+\dfrac{1}{2}×10×{4}^{2}\mathrm{m}=40\mathrm{m} $ .
(2) 设小车末端 $ N $ 到达抛出点正下方的时间为 $ {t}_{2} $ ,则有
$ L+s=\dfrac{1}{2}{a}_{1}{t}_{2}^{2} $ ,
解得 $ {t}_{2}=3\mathrm{s} $ ,
小车末端 $ N $ 到达抛出点正下方时速度为 $ v={a}_{1}{t}_{2}=6\mathrm{m}/\mathrm{s} $ ,
若小车末端 $ N $ 刚好回到抛出点正下方,则有
$ v (t-{t}_{2} )-\dfrac{1}{2}a{\prime }_{2} (t-{t}_{2})^{2}=0 $ ,
解得 $ a{\prime }_{2}=12\mathrm{m}/{\mathrm{s}}^{2} $ ,
若小车前端 $ M $ 刚好回到抛出点正下方,则有
$ v (t-{t}_{2} )-\dfrac{1}{2}a{″}_{2} (t-{t}_{2})^{2}=-L $ ,
解得 $ a{″}_{2}=24\mathrm{m}/{\mathrm{s}}^{2} $ ,
故 $ {a}_{2} $ 的范围为 $ 12\mathrm{m}/{\mathrm{s}}^{2}⩽ {a}_{2}⩽ 24\mathrm{m}/{\mathrm{s}}^{2} $ .


 (多选)
(多选) (多选)
(多选)