第二章高考强化
一、刷真题
1.如图所示,电动公交车做匀减速直线运动进站,连续经过 $ R $ 、 $ S $ 、 $ T $ 三点,已知 $ ST $ 间的距离是 $ RS $ 的两倍, $ RS $ 段的平均速度是 $ 10\mathrm{m}/\mathrm{s} $ , $ ST $ 段的平均速度是 $ 5\mathrm{m}/\mathrm{s} $ ,则公交车经过 $ T $ 点时的瞬时速度为( )

A. $ 3\mathrm{m}/\mathrm{s} $
B. $ 2\mathrm{m}/\mathrm{s} $
C. $ 1\mathrm{m}/\mathrm{s} $
D. $ 0.5\mathrm{m}/\mathrm{s} $
答案:C
解析:解法一(平均速度法) $ : $
公交车做匀减速直线运动,设在 $ RS $ 段运动的时间 $ {t}_{1} $ ,在 $ ST $ 段运动的时间为 $ {t}_{2} $ ,根据 $ t=\dfrac{x}{\overline{v}} $ ,可得 $ {t}_{1}:{t}_{2}=1:4 $ ,可令 $ {t}_{1}=2t $ , $ {t}_{2}=8t $ ,取公交车经过 $ R $ 点的时刻为零时刻,经过 $ T $ 点的速度为 $ {v}_{T} $ ,根据匀变速直线运动规律,可得 $ {v}_{t}=10\mathrm{m}/\mathrm{s} $ , $ {v}_{6t}=5\mathrm{m}/\mathrm{s} $ ,又 $ {v}_{t}-9at={v}_{T} $ , $ {v}_{6t}-4at={v}_{T} $ ,联立解得 $ {v}_{T}=1\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确.
解法二(公式法) $ : $
设公交车在 $ RS $ 段所用时间为 $ t $ ,则 $ t=\dfrac{x}{{\overline{v}}_{RS}} $ ;公交车在 $ ST $ 段所用时间 $ t\prime =\dfrac{2x}{{\overline{v}}_{ST}}=4t $ .根据 $ x={v}_{0}t+\dfrac{1}{2}a{t}^{2} $ ,变形得 $ \dfrac{x}{t}={v}_{0}+\dfrac{1}{2}at $ ,逆向列式,可得 $ 5\mathrm{m}/\mathrm{s}={v}_{T}+\dfrac{1}{2}a×4t $ , $ 10\mathrm{m}/\mathrm{s}=({v}_{T}+a×4t)+\dfrac{1}{2}at $ ,联立解得 $ {v}_{T}=1\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确.
2.如图所示,固定的光滑斜面上有一木板,其下端与斜面上 $ A $ 点距离为 $ L $ .木板由静止释放,若木板长度为 $ L $ ,通过 $ A $ 点的时间间隔为 $ \mathrm{\Delta }{t}_{1} $ ;若木板长度为 $ 2L $ ,通过 $ A $ 点的时间间隔为 $ \mathrm{\Delta }{t}_{2} $ . $ \mathrm{\Delta }{t}_{2}:\mathrm{\Delta }{t}_{1} $ 为( )
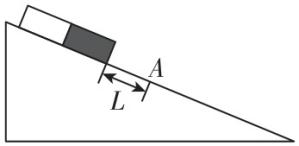
A. $ (\sqrt{3}-1):(\sqrt{2}-1) $
B. $ (\sqrt{3}-\sqrt{2}):(\sqrt{2}-1) $
C. $ (\sqrt{3}+1):(\sqrt{2}+1) $
D. $ (\sqrt{3}+\sqrt{2}):(\sqrt{2}+1) $
答案:A
解析:本题可以逆向考虑,认为木板静止不动,质点 $ A $ 向上做初速度为零的匀加速直线运动(该方法为转换对象法),根据 $ s=\dfrac{1}{2}a{t}^{2} $ 可得质点 $ A $ 通过连续相等的位移 $ L $ 所用时间之比为 $ {t}_{1}:{t}_{2}:{t}_{3}=1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}) $ ,如图所示,由题意可知, $ \mathrm{\Delta }{t}_{1}={t}_{2} $ , $ \mathrm{\Delta }{t}_{2}={t}_{2}+{t}_{3} $ ,则 $ \mathrm{\Delta }{t}_{2}:\mathrm{\Delta }{t}_{1}=(\sqrt{3}-1):(\sqrt{2}-1) $ , $ \mathrm{A} $ 正确.
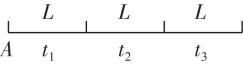
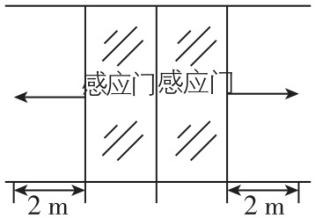
3.商场自动感应门如图所示,人走进时两扇门从静止开始同时向左右平移,经 $ 4\mathrm{s} $ 恰好完全打开,两扇门移动距离均为 $ 2\mathrm{m} $ ,若门从静止开始以相同加速度大小先匀加速运动后匀减速运动,完全打开时速度恰好为0,则加速度的大小为( )
A. $ 1.25\mathrm{m}/{\mathrm{s}}^{2} $
B. $ 1\mathrm{m}/{\mathrm{s}}^{2} $
C. $ 0.5\mathrm{m}/{\mathrm{s}}^{2} $
D. $ 0.25\mathrm{m}/{\mathrm{s}}^{2} $
答案:C
解析:设加速度的大小为 $ a $ ,根据题意可知匀加速运动与匀减速运动过程对称,根据 $ s=\dfrac{1}{2}a{t}^{2} $ 可得 $ 1\mathrm{m}=\dfrac{1}{2}a\cdot (2\mathrm{s})^{2} $ ,解得加速度大小 $ a=0.5\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{C} $ 正确.
4.为抢救病人,一辆救护车紧急出发,鸣着笛沿水平直路从 $ t=0 $ 时由静止开始做匀加速运动,加速度大小 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,在 $ {t}_{1}=10\mathrm{s} $ 时停止加速开始做匀速运动,之后某时刻救护车停止鸣笛, $ {t}_{2}=41\mathrm{s} $ 时在救护车出发处的人听到救护车发出的最后的鸣笛声.已知声速 $ {v}_{0}=340\mathrm{m}/\mathrm{s} $ ,求:
(1) 救护车匀速运动时的速度大小;
(2) 在停止鸣笛时救护车距出发处的距离.
答案:(1) $ 20\mathrm{m}/\mathrm{s} $
(2) $ 680\mathrm{m} $
解析:(1) 救护车在 $ {t}_{1}=10\mathrm{s} $ 时停止加速,则救护车匀速运动时速度为 $ v=a{t}_{1} $ ,解得 $ v=20\mathrm{m}/\mathrm{s} $ .
(2) 设匀速运动时间 $ \mathrm{\Delta }t $ 时停止鸣笛,此时救护车距出发点的距离为 $ x=\dfrac{1}{2}a{t}_{1}^{2}+v\mathrm{\Delta }t $ ,
发出的鸣笛声从停止鸣笛处传播到救护车出发点处,传播距离为 $ x={v}_{0}({t}_{2}-{t}_{1}-\mathrm{\Delta }t) $ ,解得 $ x=680\mathrm{m} $ .
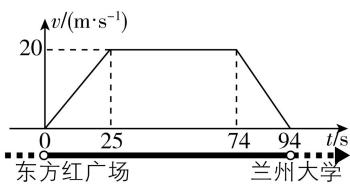
5.小明测得兰州地铁一号线列车从“东方红广场”到“兰州大学”站的 $ v-t $ 图像如图所示,此两站间的距离约为( )
A. $ 980\mathrm{m} $
B. $ 1230\mathrm{m} $
C. $ 1430\mathrm{m} $
D. $ 1880\mathrm{m} $
答案:C
解析:在 $ v-t $ 图像中,图线与时间轴所围图形的面积表示位移,则两站间的距离为 $ x=\dfrac{(74-25)+94}{2}×20\mathrm{m}=1430\mathrm{m} $ , $ \mathrm{C} $ 正确.
6.某公司在封闭公路上对一新型电动汽车进行直线加速和刹车性能测试,某次测试的速度—时间图像如图所示.已知 $ 0\sim 3.0\mathrm{s} $ 和 $ 3.5\sim 6.0\mathrm{s} $ 内图线为直线, $ 3.0\sim 3.5\mathrm{s} $ 内图线为曲线,则该车( )
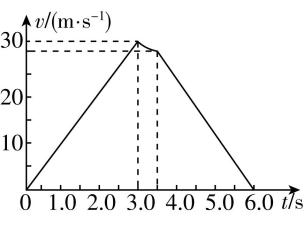
A.在 $ 0\sim 3.0\mathrm{s} $ 内的平均速度大小为 $ 10\mathrm{m}/\mathrm{s} $
B.在 $ 3.0\sim 6.0\mathrm{s} $ 内做匀减速直线运动
C.在 $ 0\sim 3.0\mathrm{s} $ 内的位移大小比在 $ 3.0\sim 6.0\mathrm{s} $ 内的大
D.在 $ 0\sim 3.0\mathrm{s} $ 内的加速度大小比在 $ 3.5\sim 6.0\mathrm{s} $ 内的小
答案:D
解析:根据 $ v-t $ 图像知,在 $ 0\sim 3.0\mathrm{s} $ 内汽车做匀加速直线运动,平均速度大小为 $ \overline{v}=\dfrac{0+30}{2}\mathrm{m}/\mathrm{s}=15\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 错误;根据 $ v-t $ 图像知,在 $ 3.0\sim 3.5\mathrm{s} $ 内速度—时间图像为曲线,汽车做非匀变速运动,在 $ 3.5\sim 6.0\mathrm{s} $ 内图像为倾斜的直线,汽车做匀减速直线运动, $ \mathrm{B} $ 错误;根据 $ v-t $ 图像与横轴围成的面积表示位移大小,在题图中作辅助线,如图所示,在 $ 0\sim 3.0\mathrm{s} $ 内汽车的位移大小为 $ {x}_{1}=\dfrac{1}{2}×30×3\mathrm{m}=45\mathrm{m} $ ,在 $ 3.0\sim 6.0\mathrm{s} $ 内汽车的位移大小 $ {x}_{2} > \dfrac{1}{2}×30×(6-3)\mathrm{m}=45\mathrm{m} $ ,可知汽车在 $ 0\sim 3.0\mathrm{s} $ 内的位移比在 $ 3.0\sim 6.0\mathrm{s} $ 内的小, $ \mathrm{C} $ 错误; $ v-t $ 图像的切线斜率绝对值表示加速度大小,在 $ 0\sim 3.0\mathrm{s} $ 内汽车加速度为 $ {a}_{1}=\dfrac{30}{3}\mathrm{m}/{\mathrm{s}}^{2}=10\mathrm{m}/{\mathrm{s}}^{2} $ ,在 $ 3.5\sim 6\mathrm{s} $ 内汽车加速度约为 $ {a}_{2}=\dfrac{0-29}{6-3.5}\mathrm{m}/{\mathrm{s}}^{2}=-11.6\mathrm{m}/{\mathrm{s}}^{2} $ ,负号表示加速度方向与初速度方向相反,则汽车在 $ 0\sim 3.0\mathrm{s} $ 内的加速度大小比在 $ 3.5\sim 6.0\mathrm{s} $ 内的小, $ \mathrm{D} $ 正确.

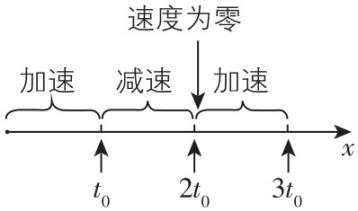
7. $ t=0 $ 时刻,质点 $ P $ 从原点由静止开始做直线运动,其加速度 $ a $ 随时间 $ t $ 按图示的正弦曲线变化,周期为 $ 2{t}_{0} $ .在 $ 0\sim 3{t}_{0} $ 时间内,下列说法正确的是( )
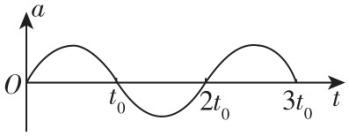 (多选)
(多选)
A. $ t=2{t}_{0} $ 时, $ P $ 回到原点
B. $ t=2{t}_{0} $ 时, $ P $ 的运动速度最小
C. $ t={t}_{0} $ 时, $ P $ 到原点的距离最远
D. $ t=\dfrac{3}{2}{t}_{0} $ 时, $ P $ 的运动速度与 $ t=\dfrac{1}{2}{t}_{0} $ 时相同
答案:BD
解析: $ a-t $ 图像中图线与 $ t $ 轴围成图形的面积表示速度的变化量,质点的运动情况描述如图所示.质点 $ P $ 一直沿 $ x $ 轴向右运动,且在 $ t=2{t}_{0} $ 时刻, $ P $ 的运动速度最小(为零), $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确; $ t=3{t}_{0} $ 时刻, $ P $ 点到原点的距离最远, $ \mathrm{C} $ 错误; $ t=\dfrac{3}{2}{t}_{0} $ 时刻,质点向右减速, $ t=\dfrac{1}{2}{t}_{0} $ 时刻,质点向右加速,运动方向相同,且两时刻到 $ t={t}_{0} $ 时刻间的图线与 $ t $ 轴围成的图像面积大小相等,所以在这两时刻 $ P $ 的运动速度大小也相等, $ \mathrm{D} $ 正确.
8.智能手机内置很多传感器,磁传感器是其中一种.现用智能手机内的磁传感器结合某应用软件,利用长直木条的自由落体运动测量重力加速度.主要步骤如下:
(1)在长直木条内嵌入7片小磁铁,最下端小磁铁与其他小磁铁间的距离如图(a)所示.
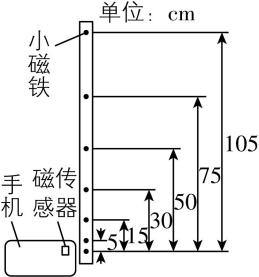
图(a)
(2)开启磁传感器,让木条最下端的小磁铁靠近该磁传感器,然后让木条从静止开始沿竖直
方向自由下落.
(3)以木条释放瞬间为计时起点,记录下各小磁铁经过传感器的时刻,数据如下表所示:
$ ℎ(\mathrm{m}) $ | 0.00 | 0.05 | 0.15 | 0.30 | 0.50 | 0.75 | 1.05 |
$ t(\mathrm{s}) $ | 0.000 | 0.101 | 0.175 | 0.247 | 0.319 | 0.391 | 0.462 |
(4) 根据表中数据,补全图(b)中的数据点,并用平滑曲线绘制下落高度 $ ℎ $ 随时间 $ t $ 变化的 $ ℎ-t $ 图线.
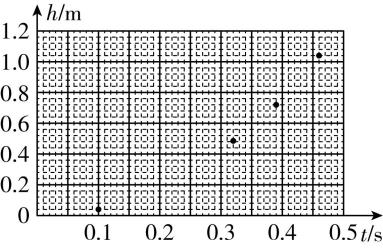
图(b)
(5) 由绘制的 $ ℎ-t $ 图线可知,下落高度随时间的变化是 (填“线性”或“非线性”)关系.
(6) 将表中数据利用计算机拟合出下落高度 $ ℎ $ 与时间的平方 $ {t}^{2} $ 的函数关系式为 $ ℎ=4.916{t}^{2}(\mathrm{S}\mathrm{I}) $ .据此函数可得重力加速度大小为 $ \mathrm{m}/{\mathrm{s}}^{2} $ .(结果保留3位有效数字)
答案:(4) 见解析
(5) 非线性
(6) 9.83
解析:(4) 如图所示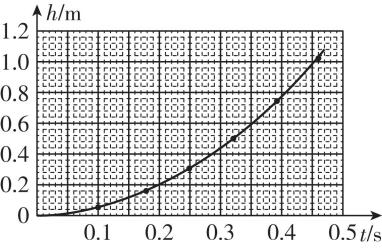
(5) 由绘制的 $ ℎ-t $ 图线可知,下落高度随时间的变化是非线性关系.
(6) 由 $ ℎ=\dfrac{1}{2}g{t}^{2} $ 可知, $ \dfrac{1}{2}g=4.916\mathrm{m}/{\mathrm{s}}^{2} $ ,解得 $ g\approx 9.83\mathrm{m}/{\mathrm{s}}^{2} $ .
二、刷原创
1.甲、乙两物体沿同一直线运动,甲的 $ v-t $ 图像、乙的 $ x-t $ 图像分别如图1、2所示,甲从坐标原点出发.下列说法正确的是( )
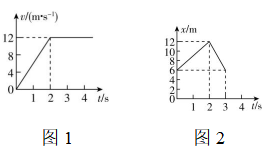 (多选)
(多选)
A. $ 0\sim 2\mathrm{s} $ 内甲、乙均做沿 $ x $ 轴正方向的匀加速直线运动
B.前 $ 2\mathrm{s} $ 内,甲、乙间的最大距离为 $ 6.75\mathrm{m} $
C. $ 2\mathrm{s} $ 时甲、乙的位置坐标均为 $ x=12\mathrm{m} $
D. $ 3\mathrm{s} $ 时甲、乙间的距离为 $ 18\mathrm{m} $
答案:BCD
解析:由题图可知 $ 0\sim 2\mathrm{s} $ 内乙做沿 $ x $ 轴正方向的匀速直线运动,甲做沿 $ x $ 轴正方向的匀加速直线运动, $ \mathrm{A} $ 错误;前 $ 2\mathrm{s} $ 内,甲在后做初速度为0、加速度大小为 $ a=\dfrac{12}{2}\mathrm{m}/{\mathrm{s}}^{2}=6\mathrm{m}/{\mathrm{s}}^{2} $ 的匀加速直线运动,乙在前从 $ x=6\mathrm{m} $ 的位置开始做速度大小为 $ v=\dfrac{12-6}{2}\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ 的匀速直线运动,当甲、乙速度相等时相距最远,有 $ v=at $ ,解得 $ t=0.5\mathrm{s} $ ,此时甲、乙间的最大距离为 $ \mathrm{\Delta }x={x}_{乙}+6\mathrm{m}-{x}_{甲}=vt+6\mathrm{m}-\dfrac{1}{2}a{t}^{2}=6.75\mathrm{m} $ , $ \mathrm{B} $ 正确; $ 2\mathrm{s} $ 内甲的位移 $ {x}_{甲1}=\dfrac{1}{2}a{t}_{1}^{2}=12\mathrm{m} $ ,因此 $ 2\mathrm{s} $ 时甲的位置坐标为 $ 12\mathrm{m} $ ,由题图2可知 $ 2\mathrm{s} $ 时乙的位置坐标也为 $ 12\mathrm{m} $ , $ \mathrm{C} $ 正确; $ 2\mathrm{s} $ 开始,甲沿 $ x $ 轴正方向做匀速直线运动, $ 2\sim 3\mathrm{s} $ 内, $ {x}_{甲2}={v}_{甲}t\prime =12×1\mathrm{m}=12\mathrm{m} $ , $ 3\mathrm{s} $ 时乙回到出发点,因此 $ 3\mathrm{s} $ 时甲、乙间的距离为 $ {x}_{甲1}+{x}_{甲2}-6\mathrm{m}=18\mathrm{m} $ , $ \mathrm{D} $ 正确.
2.如图所示,小球甲从水平地面竖直向上抛出,同一时刻小球乙开始自由下落(两小球不相碰).甲的初速度大小为 $ {v}_{0}=6\mathrm{m}/\mathrm{s} $ ,乙距地面的高度为 $ H=5\mathrm{m} $ ,重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,不计空气阻力.求:
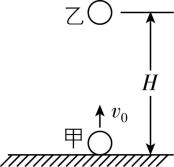
(1) 乙下落 $ 0.6\mathrm{s} $ 时,甲、乙间的竖直距离;
(2) 乙落地时,甲的速度大小及方向;
(3) 甲、乙在空中到达同一高度时,乙距地面的距离.
答案:(1) $ 1.4\mathrm{m} $
(2) $ 4\mathrm{m}/\mathrm{s} $ ,方向竖直向下
(3) $ \dfrac{55}{36}\mathrm{m} $
解析:(1) 由运动学公式有 $ {ℎ}_{乙}=\dfrac{1}{2}g{t}^{2} $ , $ {ℎ}_{甲}={v}_{0}t-\dfrac{1}{2}g{t}^{2} $ , $ \mathrm{\Delta }ℎ=H-{ℎ}_{甲}-{ℎ}_{乙} $ ,
解得 $ \mathrm{\Delta }ℎ=1.4\mathrm{m} $ .
(2) 由运动学公式有 $ H=\dfrac{1}{2}g{t}_{乙}^{2} $ ,解得 $ {t}_{乙}=1\mathrm{s} $ ,
甲上升到最高点的时间 $ {t}_{上}=\dfrac{{v}_{0}}{g}=0.6\mathrm{s} $ ,可知乙落地时,甲向下运动,此时甲的速度大小为 $ {v}_{甲}=g({t}_{乙}-{t}_{上})=4\mathrm{m}/\mathrm{s} $ ,方向竖直向下.
(3) 设经 $ {t}_{0} $ 时间甲、乙在空中达到同一高度,
由运动学公式有 $ {ℎ}_{乙1}=\dfrac{1}{2}g{t}_{0}^{2} $ , $ {ℎ}_{甲1}={v}_{0}{t}_{0}-\dfrac{1}{2}g{t}_{0}^{2} $ , $ {ℎ}_{甲1}+{ℎ}_{乙1}=H $ ,
解得 $ {ℎ}_{乙1}=\dfrac{125}{36}\mathrm{m} $ ,
故甲、乙在空中达到同一高度时,乙距地面的距离为 $ ℎ=H-{ℎ}_{乙1}=\dfrac{55}{36}\mathrm{m} $ .


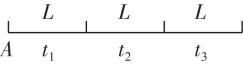




 (多选)
(多选)



 (多选)
(多选)