课时2 弹力
一、刷基础
1.关于弹力,下列说法中正确的是( )
A.物体互相接触,就有相互作用的弹力
B.放在桌面上的木块受到桌面对它向上的弹力,这是由于木块发生微小形变产生的
C.由胡克定律可知弹簧的劲度系数与弹力大小成正比,与形变量成反比
D.压力和支持力的方向都垂直于物体的接触面,绳的拉力沿绳指向绳收缩的方向
答案:D
解析:互相接触的物体只有发生弹性形变时才会产生弹力, $ \mathrm{A} $ 错误;放在桌面上的木块受到桌面对它向上的弹力,这是由于桌面发生微小形变产生的, $ \mathrm{B} $ 错误;弹簧的劲度系数只与弹簧本身有关,与弹力及形变量无关, $ \mathrm{C} $ 错误;压力和支持力的方向都垂直于物体的接触面,绳的拉力沿绳指向绳收缩的方向, $ \mathrm{D} $ 正确.
2.下列关于形变的说法正确的是( )(多选)
A.弓张紧时所发生的形变是弹性形变
B.用力将一根直铁丝弯折成“ ”形发生的形变为弹性形变
”形发生的形变为弹性形变
C.甲、乙两车相撞后甲车的车头凹下去了,甲车头所发生的形变是塑性形变
D.骑自行车时车上的减震弹簧所发生的形变是塑性形变
答案:AC
解析:发生形变的物体在撤去外力后能恢复原状的形变称为弹性形变,不能恢复或不能完全恢复原状的形变称为塑性形变,则弓张紧时所发生的形变和骑自行车时车上的减震弹簧所发生的形变是弹性形变,铁丝弯折成“ ”形发生的形变和相撞后凹下去的车头所发生的形变是塑性形变.故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确.
”形发生的形变和相撞后凹下去的车头所发生的形变是塑性形变.故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确.
3.关于下列四图中的弹力(小球均处于静止状态),下列说法正确的是( )
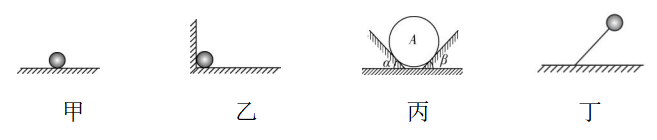 (多选)
(多选)
A.图甲中,球对水平地面的弹力就是球的重力
B.图乙中,当水平地面光滑时,竖直墙壁对球没有弹力
C.图丙中,两斜面与水平地面的夹角分别为 $ \alpha $ 、 $ \beta $ , $ A $ 对两斜面均有压力作用
D.图丁中,轻杆对球的弹力方向竖直向上
答案:BCD
解析:弹力与重力是不同性质的力,题图甲中,只能说球对水平地面的弹力大小等于球的重力大小, $ \mathrm{A} $ 错误;题图乙中,当水平地面光滑时,假设竖直墙壁对球有弹力,则水平方向球受力不平衡,则球不能静止,故假设不成立,即竖直墙壁对球没有弹力, $ \mathrm{B} $ 正确;题图丙中,若除去左侧的斜面, $ A $ 将运动,若除去右侧的斜面, $ A $ 也将运动,所以两斜面对 $ A $ 均有弹力作用,即 $ A $ 对两斜面均有压力作用, $ \mathrm{C} $ 正确;题图丁中,球在竖直方向受力平衡,则轻杆对球的弹力方向竖直向上,大小等于球的重力大小, $ \mathrm{D} $ 正确.
4.下列对图中弹力的判断正确的是( )
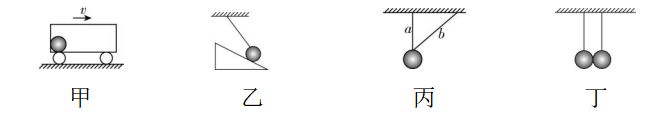
A.图甲中,小球随车厢一起向右做匀速直线运动,车厢左壁对小球有弹力
B.图乙中,小球被轻绳斜拉着静止在光滑的斜面上,斜面对小球有弹力,该弹力是由小球形变引起的
C.图丙中,小球被 $ a $ 、 $ b $ 两轻绳悬挂着处于静止状态,其中 $ a $ 绳竖直,对小球有弹力,该弹力由 $ a $ 绳形变引起; $ b $ 绳对小球无弹力
D.图丁中,两相同球各自被长度一样的竖直轻绳拉住而静止,则两球间有弹力
答案:C
解析:题图甲中,小球随车厢一起向右做匀速直线运动,车厢左壁对小球没有弹力,否则小球不可能处于平衡状态,故 $ \mathrm{A} $ 错误;题图乙中,小球被轻绳斜拉着静止在光滑的斜面上,斜面对小球有弹力,该弹力是由斜面形变引起的,故 $ \mathrm{B} $ 错误;题图丙中,小球被 $ a $ 、 $ b $ 两轻绳悬挂着处于静止状态,其中 $ a $ 绳竖直,对小球有弹力,该弹力由 $ a $ 绳形变引起,那么 $ b $ 绳对小球没有弹力,否则小球会向右运动,故 $ \mathrm{C} $ 正确;题图丁中,两相同球各自被长度一样的竖直轻绳拉住而静止,由于轻绳均竖直,根据弹力产生的条件可知,两球间没有弹力,故 $ \mathrm{D} $ 错误.
5.下列各实例中力的方向描述正确的是( )
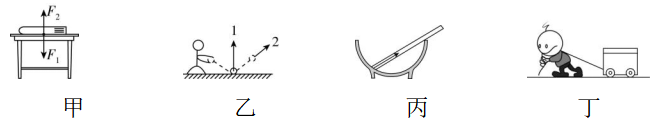 (多选)
(多选)
A.甲图中,由于书的形变,对桌面产生向上的弹力 $ {F}_{2} $
B.乙图中,篮球与光滑地面作用时,地面对篮球的弹力如图中1所示
C.丙图中,碗对筷子的弹力沿筷子斜向上,如图中箭头所示
D.丁图中,绳的拉力沿着绳而指向绳收缩的方向
答案:BD
解析:题图甲中,由于书的形变,对桌面产生向下的弹力 $ {F}_{1} $ , $ \mathrm{A} $ 错误;题图乙中,篮球与光滑地面作用时,地面对篮球的弹力垂直接触面竖直向上,如题图乙中1所示, $ \mathrm{B} $ 正确;题图丙中,碗对筷子的弹力应该垂直于过接触点的切线指向碗所在圆的圆心, $ \mathrm{C} $ 错误;题图丁中,绳的拉力沿着绳而指向绳收缩的方向, $ \mathrm{D} $ 正确.
6.下列各图中物体 $ A $ 均静止,请在图中画出物体 $ A $ 所受弹力的示意图.
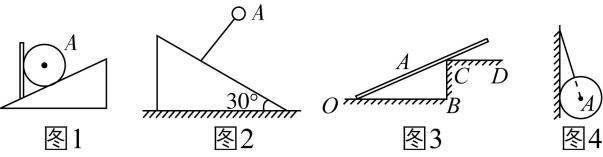
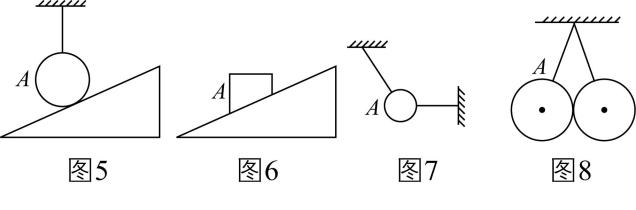
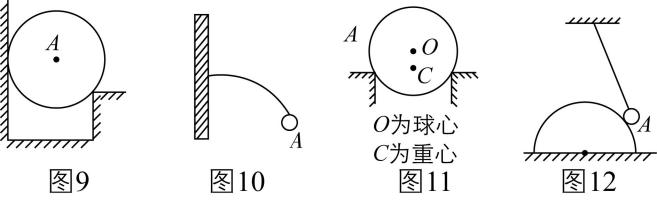
答案:如图所示


解析:
7.如图所示,四根劲度系数都为 $ 50\mathrm{N}/\mathrm{m} $ 的相同轻质弹簧,右端都用 $ 20\mathrm{N} $ 的水平力往右拉.甲左端固定在墙壁上,乙左端用 $ 20\mathrm{N} $ 的水平力往左拉,丙左端拉着物体向右匀速运动,丁左端拉着物体向右加速运动.弹簧均为弹性形变.下列关于弹簧伸长量 $ \mathrm{\Delta }l $ 的说法正确的是( )

A. $ \mathrm{\Delta }{l}_{甲}=0.4\mathrm{m}\mathrm{\Delta }{l}_{乙}=0.8\mathrm{m}\mathrm{\Delta }{l}_{丙} > 0.4\mathrm{m}\mathrm{\Delta }{l}_{丁}=0.4\mathrm{m} $
B. $ \mathrm{\Delta }{l}_{甲}=0.4\mathrm{m}\mathrm{\Delta }{l}_{乙}=0.8\mathrm{m}\mathrm{\Delta }{l}_{丙}=0.4\mathrm{m}\mathrm{\Delta }{l}_{丁} > 0.4\mathrm{m} $
C. $ \mathrm{\Delta }{l}_{甲}=0.4\mathrm{m}\mathrm{\Delta }{l}_{乙}=0.4\mathrm{m}\mathrm{\Delta }{l}_{丙}=0.4\mathrm{m}\mathrm{\Delta }{l}_{丁}=0.4\mathrm{m} $
D. $ \mathrm{\Delta }{l}_{甲}=0.4\mathrm{m}\mathrm{\Delta }{l}_{乙}=0.4\mathrm{m}\mathrm{\Delta }{l}_{丙} > 0.4\mathrm{m}\mathrm{\Delta }{l}_{丁} > 0.4\mathrm{m} $
答案:C
解析:由于施加的拉力均为 $ 20\mathrm{N} $ ,所以弹簧弹力均为 $ 20\mathrm{N} $ ,则弹簧的伸长量相等,均为 $ \mathrm{\Delta }l=\dfrac{F}{k}=\dfrac{20}{50}\mathrm{m}=0.4\mathrm{m} $ ,故选 $ \mathrm{C} $ .
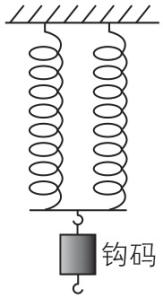
8.将一轻质弹簧上端固定,下端悬挂一钩码,静止时弹簧伸长了 $ l $ .如果将该轻质弹簧从正中间剪断,再将上端连在一起并固定,下端连在一起,在下端悬挂同样的钩码,如图所示.若弹簧始终在弹性限度内,则静止时,每一段弹簧将伸长( )
A. $ \dfrac{1}{4}l $
B. $ \dfrac{1}{2}l $
C. $ l $
D. $ 2l $
答案:A
解析:当轻弹簧从正中间剪断时,弹簧的劲度系数变为原来的两倍,设钩码质量为 $ m $ ,剪断前有 $ mg=kl $ ,剪断后,对每一段弹簧都有 $ \dfrac{1}{2}mg=2k\cdot x $ ,解得 $ x=\dfrac{mg}{4k}=\dfrac{1}{4}l $ ,故 $ \mathrm{A} $ 正确.
9.如图所示,一根弹簧挂上 $ 20\mathrm{N} $ 的重物,重物静止时指针 $ P $ 正对刻度尺的 $ 3\mathrm{c}\mathrm{m} $ 位置;更换 $ 30\mathrm{N} $ 重物后,重物静止时指针 $ P $ 正对刻度尺的 $ 4\mathrm{c}\mathrm{m} $ 位置,弹簧没有超出弹性限度,则( )
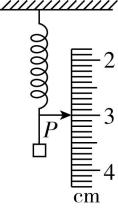
A.挂上 $ 50\mathrm{N} $ 重物,重物静止时指针 $ P $ 正对刻度尺的 $ 5\mathrm{c}\mathrm{m} $ 位置
B.弹簧的劲度系数为 $ 10\mathrm{N}/\mathrm{m} $
C.未悬挂重物时,指针 $ P $ 正对刻度尺的 $ 1\mathrm{c}\mathrm{m} $ 位置
D.未悬挂重物时,指针 $ P $ 正对刻度尺的 $ 0\mathrm{c}\mathrm{m} $ 位置
答案:C
解析:设未悬挂重物时,指针 $ P $ 正对刻度尺的 $ {x}_{0} $ 位置,根据胡克定律有 $ {F}_{1}=k({x}_{1}-{x}_{0})=20\mathrm{N} $ , $ {F}_{2}=k({x}_{2}-{x}_{0})=30\mathrm{N} $ ,其中 $ {x}_{1}=3\mathrm{c}\mathrm{m} $ , $ {x}_{2}=4\mathrm{c}\mathrm{m} $ ,联立解得 $ k=1000\mathrm{N}/\mathrm{m} $ , $ {x}_{0}=1\mathrm{c}\mathrm{m} $ ,故 $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误, $ \mathrm{C} $ 正确;根据胡克定律有 $ {F}_{3}=k({x}_{3}-{x}_{0})=50\mathrm{N} $ ,解得 $ {x}_{3}=6\mathrm{c}\mathrm{m} $ ,故挂上 $ 50\mathrm{N} $ 重物,重物静止时指针 $ P $ 正对刻度尺的 $ 6\mathrm{c}\mathrm{m} $ 位置,故 $ \mathrm{A} $ 错误.
10.如图所示为一轻质弹簧的弹力随长度变化的关系图像(轻质弹簧未超过弹性限度),下列说法不正确的是( )
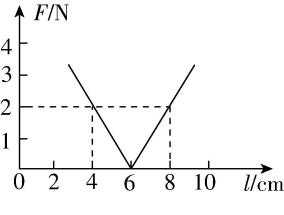
A.弹簧的原长为 $ 6\mathrm{c}\mathrm{m} $
B.弹簧的劲度系数为 $ 50\mathrm{N}/\mathrm{m} $
C.弹簧的长度为 $ 0.16\mathrm{m} $ 时,弹力的大小为 $ 10\mathrm{N} $
D.弹簧两端各加 $ 4\mathrm{N} $ 拉力时,弹簧的长度为 $ 10\mathrm{c}\mathrm{m} $
答案:B
解析:由题图可知,当弹簧的长度为 $ 6\mathrm{c}\mathrm{m} $ 时,弹簧的弹力为零,则弹簧的原长为 $ 6\mathrm{c}\mathrm{m} $ , $ \mathrm{A} $ 正确;弹簧的劲度系数为 $ k=\dfrac{\mathrm{\Delta }F}{\mathrm{\Delta }l}=\dfrac{2-0}{(8-6)×{10}^{-2}}\mathrm{N}/\mathrm{m}=100\mathrm{N}/\mathrm{m} $ , $ \mathrm{B} $ 错误;弹簧的长度为 $ 0.16\mathrm{m} $ 时,弹力的大小为 $ F=100×(0.16-0.06)\mathrm{N}=10\mathrm{N} $ , $ \mathrm{C} $ 正确;弹簧两端各加 $ 4\mathrm{N} $ 拉力时,弹簧的弹力为 $ 4\mathrm{N} $ ,则弹簧的伸长量为 $ \mathrm{\Delta }l\prime =\dfrac{4}{100}\mathrm{m}=0.04\mathrm{m}=4\mathrm{c}\mathrm{m} $ ,则弹簧的长度为 $ l={l}_{0}+\mathrm{\Delta }l\prime =6\mathrm{c}\mathrm{m}+4\mathrm{c}\mathrm{m}=10\mathrm{c}\mathrm{m} $ , $ \mathrm{D} $ 正确.本题选说法不正确的,故选 $ \mathrm{B} $ .
11.如图所示, $ A $ 、 $ B $ 、 $ C $ 三个物体叠放在水平地面上处于静止状态,以下说法正确的是( )
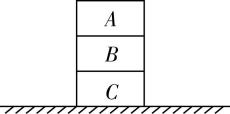
A.物体 $ A $ 对 $ C $ 有向下的压力作用
B.物体 $ A $ 和 $ B $ 对地面都有压力作用
C.地面对 $ C $ 的支持力是由于地面发生形变要恢复原状产生的
D.物体 $ A $ 对 $ B $ 的压力是 $ A $ 的重力
答案:C
解析:根据弹力产生的条件可知,弹力是接触力,因此 $ A $ 对 $ C $ 没有压力作用, $ A $ 和 $ B $ 对地面也没有压力作用,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;物体由于发生了弹性形变,要恢复原状,会对与它接触的物体产生弹力,因此地面对 $ C $ 的支持力是由于地面发生形变要恢复原状产生的,故 $ \mathrm{C} $ 正确; $ A $ 对 $ B $ 的压力与 $ A $ 的重力不是同一性质的力,故 $ \mathrm{D} $ 错误.
12.静止的车厢顶部用细线竖直悬挂一小球,如图所示,小球下方与一光滑斜面接触.关于小球的受力,下列说法正确的是( )
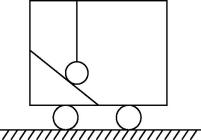
A.细线可能对小球没有拉力作用
B.小球受重力、细线对它的拉力和斜面对它的弹力
C.细线对小球有拉力,这个拉力是细线发生形变产生的
D.斜面对小球可能有弹力
答案:C
解析:假设细线对小球没有拉力,则小球受到重力和斜面的弹力不能平衡,假设不成立,故 $ \mathrm{A} $ 错误;小球和光滑斜面接触,假设斜面对小球有弹力,小球将受到三个力作用,重力和细线的拉力在竖直方向上,斜面的弹力垂直于斜面向上,则小球不能静止,故斜面对小球没有弹力,故 $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误;细线对小球有拉力,这个拉力是细线发生形变产生的,故 $ \mathrm{C} $ 正确.
二、刷提升
1.如图所示,底端置于粗糙水平地面上的直杆,其顶端通过一根水平细线被手拉住,杆处于静止状态.下列说法正确的是( )
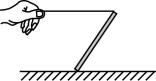 (多选)
(多选)
A.细线对杆的弹力方向水平向右
B.细线对杆的弹力是由细线的形变产生的
C.杆受到地面的弹力是由地面的形变产生的
D.地面对杆的弹力方向沿杆向左下方
答案:BC
解析:细线对杆的弹力方向沿着细线收缩的方向,则细线对杆的弹力方向水平向左,故 $ \mathrm{A} $ 错误;细线对杆的弹力的施力物体是细线,细线对杆的弹力是由细线的形变产生的,故 $ \mathrm{B} $ 正确;杆受到地面弹力的施力物体是地面,杆受到地面的弹力是由地面的形变产生的,故 $ \mathrm{C} $ 正确;杆受到地面的弹力方向垂直于接触面,即垂直地面向上,故 $ \mathrm{D} $ 错误.
2.图中各物体均处于静止状态.图中画出了小球 $ A $ 所受弹力的情况,其中正确的是( )
A.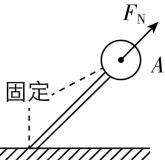
B.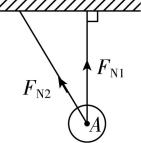
C.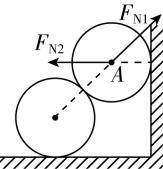
D.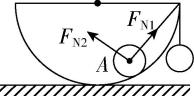
答案:C
解析:选项 $ \mathrm{A} $ 中小球受重力和杆的弹力处于静止状态,由二力平衡可得小球受到杆的弹力应竖直向上, $ \mathrm{A} $ 错误.选项 $ \mathrm{B} $ 中因为右边的绳竖直,如果左边的绳有拉力,小球不能静止,所以左边的绳没有拉力, $ \mathrm{B} $ 错误.球与球接触的弹力方向垂直于过接触点的公切面(即在两球心的连线上)指向受力物体,球与面接触的弹力过接触点垂直于面指向球心, $ \mathrm{C} $ 正确.选项 $ \mathrm{D} $ 中大半圆对小球的支持力 $ {F}_{\mathrm{N}2} $ 应是沿小球的球心与大半圆的圆心连线指向大半圆的圆心, $ \mathrm{D} $ 错误.
3.一根轻质弹性绳(产生的弹力与其伸长量满足胡克定律)的一端固定在水平天花板上,其自然伸直的长度为 $ 72\mathrm{c}\mathrm{m} $ ,若将一钩码(重力为 $ G $ )挂在弹性绳的下端,平衡时弹性绳的总长度为 $ 80\mathrm{c}\mathrm{m} $ ;若将弹性绳的两端固定在天花板上的同一点,将同样的钩码挂在弹性绳的中点,平衡时弹性绳的总长度变为(弹性绳始终处于弹性限度内,不考虑挂钩处的摩擦)( )
A. $ 74\mathrm{c}\mathrm{m} $
B. $ 76\mathrm{c}\mathrm{m} $
C. $ 80\mathrm{c}\mathrm{m} $
D. $ 88\mathrm{c}\mathrm{m} $
答案:B
解析:设弹性绳的原长为 $ {l}_{0} $ ,劲度系数为 $ k $ ,第一次挂钩码时,根据胡克定律有 $ k(l-{l}_{0})=G $ ,将弹性绳的两端固定在天花板上的同一点,将同样的钩码挂在弹性绳的中点,根据平衡条件有 $ 2F=G $ ,根据胡克定律有 $ F=k\mathrm{\Delta }l $ ,解得 $ \mathrm{\Delta }l=\dfrac{l-{l}_{0}}{2}=4\mathrm{c}\mathrm{m} $ ,则平衡时弹性绳总长度为 $ l\prime ={l}_{0}+\mathrm{\Delta }l=76\mathrm{c}\mathrm{m} $ , $ \mathrm{B} $ 正确.
4.两根劲度系数分别为 $ {k}_{1} $ 和 $ {k}_{2} $ 的轻质弹簧 $ a $ 、 $ b $ 串接在一起, $ a $ 弹簧的一端固定在墙上,如图所示.开始时弹簧均处于原长状态,现用水平力作用在 $ b $ 弹簧的右端向右拉动弹簧.已知 $ a $ 弹簧的伸长量为 $ L $ ,则( )
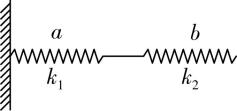
A. $ b $ 弹簧的伸长量为 $ \dfrac{{k}_{2}L}{{k}_{1}} $
B. $ b $ 弹簧所受的弹力为 $ {k}_{2}L $
C. $ b $ 弹簧的右端向右移动的距离为 $ (1+\dfrac{{k}_{2}}{{k}_{1}})L $
D. $ b $ 弹簧的右端向右移动的距离为 $ (1+\dfrac{{k}_{1}}{{k}_{2}})L $
答案:D
解析:两根轻弹簧串联,弹力大小相等,则 $ b $ 弹簧所受的弹力为 $ {F}_{b}={F}_{a}={k}_{1}L $ ,根据胡克定律可得 $ {F}_{b}={k}_{2}{x}_{b} $ ,解得 $ b $ 弹簧的伸长量为 $ {x}_{b}=\dfrac{{k}_{1}L}{{k}_{2}} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;开始时弹簧均处于原长状态,则 $ b $ 弹簧的右端向右移动的距离等于两根弹簧伸长量之和,为 $ s=L+{x}_{b}=(1+\dfrac{{k}_{1}}{{k}_{2}})L $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
5.一根大弹簧内套一根小弹簧,大弹簧比小弹簧长 $ 0.20\mathrm{m} $ ,它们的下端固定在地面上,上端自由,如图甲所示.当加力压缩此组合弹簧时,测得力和弹簧压缩距离之间的关系如图乙所示,则大弹簧和小弹簧的劲度系数分别是( )
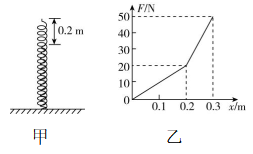
A. $ 100\mathrm{N}/\mathrm{m} $ , $ 200\mathrm{N}/\mathrm{m} $
B. $ 200\mathrm{N}/\mathrm{m} $ , $ 100\mathrm{N}/\mathrm{m} $
C. $ 100\mathrm{N}/\mathrm{m} $ , $ 300\mathrm{N}/\mathrm{m} $
D. $ 300\mathrm{N}/\mathrm{m} $ , $ 200\mathrm{N}/\mathrm{m} $
答案:A
解析:设大弹簧劲度系数为 $ {k}_{1} $ ,小弹簧劲度系数为 $ {k}_{2} $ ,根据胡克定律 $ F=k\mathrm{\Delta }x $ ,可得在 $ x=0.2\mathrm{m} $ 时,有 $ 20\mathrm{N}={k}_{1}×0.2\mathrm{m} $ ,在 $ x=0.3\mathrm{m} $ 时,有 $ 50\mathrm{N}={k}_{1}×0.3\mathrm{m}+{k}_{2}×0.1\mathrm{m} $ ,联立解得 $ {k}_{1}=100\mathrm{N}/\mathrm{m} $ , $ {k}_{2}=200\mathrm{N}/\mathrm{m} $ ,故 $ \mathrm{A} $ 正确.
6.如图甲为一竖直放置的内壁光滑的圆筒,筒下端固定一轻弹簧,2个完全相同的物块静置于弹簧上端,此时最上面的物块上表面刚好与圆筒开口平齐.现将第3个物块(与筒内物块完全相同)放入筒内,如图乙,待物块静止后,第3个物块上表面也刚好与圆筒开口平齐,已知物块的厚度为 $ d $ ,重力为 $ G $ ,弹簧始终处在弹性限度内,由此可知弹簧的劲度系数 $ k $ 为( )

A. $ \dfrac{G}{3d} $
B. $ \dfrac{2G}{3d} $
C. $ \dfrac{G}{d} $
D. $ \dfrac{2G}{d} $
答案:C
解析:设弹簧原长为 $ L $ ,放2个物块时弹簧的长度为 $ {L}_{1} $ ,根据胡克定律可知 $ 2G=k(L-{L}_{1}) $ ,将第3个物块放入筒内后 $ 3G=k(L-{L}_{1}+d) $ ,联立解得 $ k=\dfrac{G}{d} $ ,故选 $ \mathrm{C} $ .
![]() ”形发生的形变为弹性形变
”形发生的形变为弹性形变![]() ”形发生的形变和相撞后凹下去的车头所发生的形变是塑性形变.故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确.
”形发生的形变和相撞后凹下去的车头所发生的形变是塑性形变.故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确. (多选)
(多选)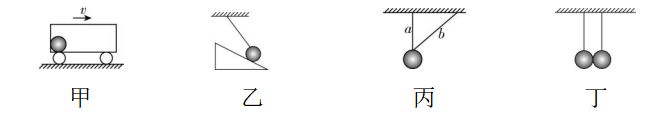
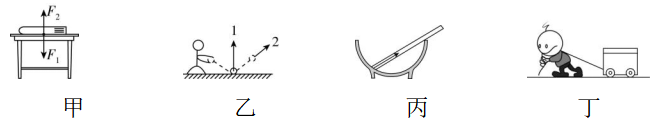 (多选)
(多选)










 (多选)
(多选)





