1．如图所示，一条长 $ 40\mathrm{c}\mathrm{m} $ 的链子对称地挂在光滑圆环上，稍加扰动，链子从右侧滑下至链子刚离开圆环的过程，下列说法正确的是（ ）
（多选）
A．链子重心下移了 $ 20\mathrm{c}\mathrm{m} $
B．链子重心下移了 $ 10\mathrm{c}\mathrm{m} $
C．下滑过程中链子重心先上移再下移
D．下滑过程中链子重心一直下移
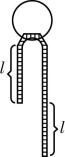
初始时链子的重心距圆环下端 $ 10\mathrm{c}\mathrm{m} $ ,刚离开圆环时,链子重心距圆环下端 $ 20\mathrm{c}\mathrm{m} $ ,则链子重心下移了 $ 10\mathrm{c}\mathrm{m} $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确；下滑过程中,可将链子左侧与链子右侧下端相同长度相互抵消,如图所示,观察右侧剩余部分,可知重心一直下移, $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
2．如图所示，一根竖直的弹簧下端连接一个光滑的小球，小球处于斜面和挡板之间，斜面、挡板均和小球接触，下列说法正确的是（ ）
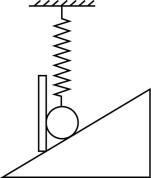（多选）
A．若小球与斜面之间有弹力，则小球与挡板之间一定有弹力
B．若小球与斜面之间有弹力，则小球与挡板之间不一定有弹力
C．若小球与挡板之间有弹力，则小球与弹簧之间一定有弹力
D．若小球与挡板之间有弹力，则小球与弹簧之间不一定有弹力
若小球与斜面之间有弹力,则斜面对小球的弹力斜向左上方,小球能够在水平方向平衡,那么小球一定受到挡板水平向右的弹力,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误；若小球与挡板之间有弹力,由上述分析可知小球也将受到斜面的弹力作用,假设弹簧对小球没有弹力,小球仍可以平衡,故小球与弹簧之间不一定有弹力,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
3．如图甲所示，力 $ F $ （未画出）变化时弹簧长度不断变化，取水平向左为正方向，得到外力 $ F $ 与弹簧长度的关系如图乙所示，则下列说法正确的是（ ）
（多选）
A．弹簧原长为 $ 15\mathrm{c}\mathrm{m} $
B．弹簧的劲度系数为 $ 4\mathrm{N}/\mathrm{m} $
C． $ l=10\mathrm{c}\mathrm{m} $ 时，弹簧对墙壁的弹力方向水平向右
D． $ l=10\mathrm{c}\mathrm{m} $ 时，弹簧对墙壁的弹力大小为 $ 20\mathrm{N} $
当 $ F=0 $ 时,弹簧的长度是原长,由题图乙可知弹簧原长为 $ 15\mathrm{c}\mathrm{m} $ ,故 $ \mathrm{A} $ 正确；由胡克定律有 $ F=kx $ ,可得弹簧的劲度系数为 $ k=\dfrac{\mathrm{\Delta }F}{\mathrm{\Delta }x}=\dfrac{40}{15-5}×{10}^{2}\mathrm{N}/\mathrm{m}=400\mathrm{N}/\mathrm{m} $ ,故 $ \mathrm{B} $ 错误； $ l=10\mathrm{c}\mathrm{m} $ 时,弹簧处于压缩状态,弹簧对墙壁的弹力方向水平向左,大小为 $ F\prime =kx\prime =400×(15-10)×{10}^{-2}\mathrm{N}=20\mathrm{N} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
4．如图所示，某同学将两根完全相同的轻质弹簧按图甲方式悬挂质量为 $ m $ 的物块，测得静止时弹簧总长为 $ {L}_{1} $ ，再将两根弹簧分别以图乙和图丙的方式悬挂两个物块，测得两种方式中的弹簧总长分别为 $ {L}_{2} $ 、 $ {L}_{3} $ ，则下列判断正确的是（ ）
A． $ {L}_{1}={L}_{2}={L}_{3} $
B． $ {L}_{1} > {L}_{2} > {L}_{3} $
C． $ {L}_{1} > {L}_{3} > {L}_{2} $
D． $ {L}_{1} < {L}_{3} < {L}_{2} $
设每根弹簧的原长为 $ L $ ,劲度系数为 $ k $ ,题图甲中弹簧的总长度为 $ {L}_{1}=2L+2\dfrac{mg}{k} $ ,题图乙中弹簧的总长度为 $ {L}_{2}=2L+\dfrac{mg}{k}+\dfrac{\dfrac{2}{3}mg}{k}=2L+\dfrac{5}{3}\cdot \dfrac{mg}{k} $ ,题图丙中弹簧的总长度为 $ {L}_{3}=2L+\dfrac{mg}{k}+\dfrac{\dfrac{1}{3}mg}{k}=2L+\dfrac{4}{3}\cdot \dfrac{mg}{k} $ ,比较可知 $ {L}_{1} > {L}_{2} > {L}_{3} $ ,故选 $ \mathrm{B} $ .
5．如图所示， $ A $ 、 $ B $ 、 $ C $ 三个物体的质量为 $ {m}_{A}=\dfrac{1}{2}{m}_{B}=\dfrac{1}{2}{m}_{C}=m $ ， $ A $ 、 $ B $ 两物体通过绳子绕过定滑轮相连， $ B $ 、 $ C $ 用劲度系数为 $ {k}_{2} $ 的弹簧乙相连，劲度系数为 $ {k}_{1} $ 的弹簧甲一端固定在天花板上，另一端与滑轮相连.开始时， $ A $ 、 $ B $ 两物体在同一水平面上，不计滑轮、绳子、弹簧的重力和一切摩擦.现用竖直向下的力缓慢拉动 $ A $ 物体，在拉动过程中，弹簧和与 $ A $ 、 $ B $ 相连的绳子始终竖直，重力加速度为 $ g $ ,到 $ C $ 物体刚要离开地面 $ (A $ 未落地， $ B $ 未与滑轮相碰 $ ) $ 时， $ A $ 、 $ B $ 两物体的高度差为（ ）
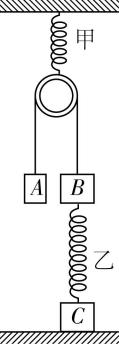
A． $ \dfrac{3mg}{{k}_{2}}+\dfrac{6mg}{{k}_{1}} $
B． $ \dfrac{3mg}{{k}_{2}}+\dfrac{12mg}{{k}_{1}} $
C． $ \dfrac{6mg}{{k}_{2}}+\dfrac{6mg}{{k}_{1}} $
D． $ \dfrac{6mg}{{k}_{2}}+\dfrac{12mg}{{k}_{1}} $
开始时,弹簧甲的弹力是 $ A $ 物体重力的两倍,所以它的伸长量 $ {x}_{1}=\dfrac{2mg}{{k}_{1}} $ ；弹簧乙的弹力是 $ A $ 、 $ B $ 两物体的重力差,所以它的压缩量 $ {x}_{2}=\dfrac{mg}{{k}_{2}} $ .当 $ C $ 物体刚要离开地面时,弹簧甲的弹力等于 $ B $ 、 $ C $ 两物体重力和的两倍,所以它的伸长量 $ x{\prime }_{1}=\dfrac{8mg}{{k}_{1}} $ ；弹簧乙的弹力等于 $ C $ 的重力,所以它的伸长量 $ x{\prime }_{2}=\dfrac{2mg}{{k}_{2}} $ ,所以 $ B $ 物体上升的高度 $ {ℎ}_{B}={x}_{2}+x{\prime }_{2}=\dfrac{3mg}{{k}_{2}} $ ,物体 $ A $ 下降的高度 $ {ℎ}_{A}={ℎ}_{B}+2(x{\prime }_{1}-{x}_{1})=\dfrac{3mg}{{k}_{2}}+\dfrac{12mg}{{k}_{1}} $ ,所以 $ A $ 、 $ B $ 的高度差 $ \mathrm{\Delta }ℎ={ℎ}_{A}+{ℎ}_{B}=\dfrac{6mg}{{k}_{2}}+\dfrac{12mg}{{k}_{1}} $ ,故 $ \mathrm{D} $ 正确.