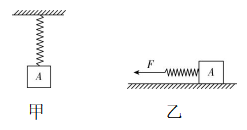课时1 滑动摩擦力
一、刷基础
1.有关滑动摩擦力,下列说法中正确的有( )(多选)
A.滑动摩擦力的方向一定与物体运动方向相反
B.有滑动摩擦力一定有正压力
C.滑动摩擦力总是与接触面上的正压力垂直
D.只有运动的物体才受滑动摩擦力作用
答案:BC
解析:滑动摩擦力的方向一定与物体相对运动的方向相反,故 $ \mathrm{A} $ 错误;当两物体相互接触并相互挤压,接触面粗糙且有相对运动时,两物体间有滑动摩擦力,故 $ \mathrm{B} $ 正确;滑动摩擦力的方向与接触面相切,而正压力垂直于接触面,则滑动摩擦力的方向跟接触面所受正压力垂直,故 $ \mathrm{C} $ 正确;静止的物体也可以受滑动摩擦力,如擦黑板时,黑板是静止的,但相对黑板擦是运动的,则黑板受滑动摩擦力作用,故 $ \mathrm{D} $ 错误.
2.如图所示, $ A $ 为长木板,在水平面上以速度 $ {v}_{1} $ 开始向右运动,同时物块 $ B $ 在 $ A $ 的上表面以速度 $ {v}_{2} $ 开始向右运动,且 $ A $ 、 $ B $ 接触面粗糙,水平面光滑.下列判断正确的是( )
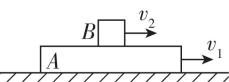
A.若 $ {v}_{1}={v}_{2} $ , $ A $ 、 $ B $ 之间无滑动摩擦力
B.若 $ {v}_{1} > {v}_{2} $ , $ A $ 受到 $ B $ 所施加的向右的滑动摩擦力
C.若 $ {v}_{1} < {v}_{2} $ , $ B $ 受到 $ A $ 所施加的向右的滑动摩擦力
D.若 $ {v}_{1} > {v}_{2} $ , $ A $ 、 $ B $ 之间无滑动摩擦力
答案:A
解析:若 $ {v}_{1}={v}_{2} $ ,则 $ A $ 、 $ B $ 相对静止, $ A $ 、 $ B $ 之间无滑动摩擦力, $ \mathrm{A} $ 正确;若 $ {v}_{1} > {v}_{2} $ ,则 $ A $ 相对 $ B $ 向右运动,故 $ B $ 对 $ A $ 施加向左的滑动摩擦力, $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误;若 $ {v}_{1} < {v}_{2} $ ,则 $ B $ 相对 $ A $ 向右运动,故 $ B $ 受到 $ A $ 施加的向左的滑动摩擦力,故 $ \mathrm{C} $ 错误.
3.如图所示,某同学骑普通自行车沿斜坡向上加速行驶,某时刻链条突然断裂,自行车开始向上减速直至速度为零,不计空气阻力、轮子转轴处的摩擦力.下列说法正确的是( )
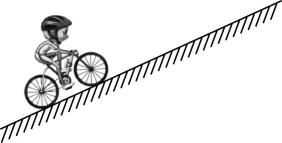
A.链条断裂前,自行车前轮受到斜坡的摩擦力方向沿斜坡向上
B.链条断裂前,自行车后轮受到斜坡的摩擦力方向沿斜坡向下
C.链条断裂后,自行车前轮受到斜坡的摩擦力方向沿斜坡向上
D.链条断裂后,自行车后轮受到斜坡的摩擦力方向沿斜坡向下
答案:D
解析:链条断裂前,自行车后轮为驱动轮,后轮受到的摩擦力方向沿斜坡向上,前轮为从动轮,受到斜坡的摩擦力方向沿斜坡向下, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;链条断裂后,自行车前、后轮都不再是驱动轮,自行车减速运动,自行车前、后轮受到斜坡的摩擦力均沿斜坡向下,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
4.风洞实验室中可产生水平方向、大小可调的风力.如图,一正方体物块静置于风洞内的水平地面上,其一面与风速垂直,风速从零开始逐渐增大,当风速为 $ 3\mathrm{m}/\mathrm{s} $ 时刚好能推动此物块.已知风对物块的推力 $ F\propto S{v}^{2} $ ,其中 $ v $ 为风速、 $ S $ 为物块迎风面积.下列说法正确的是( )
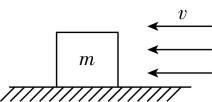 (多选)
(多选)
A.风速由 $ 1\mathrm{m}/\mathrm{s} $ 变为 $ 2\mathrm{m}/\mathrm{s} $ 时,物块受到地面的摩擦力变大
B.风速由 $ 1\mathrm{m}/\mathrm{s} $ 变为 $ 2\mathrm{m}/\mathrm{s} $ 时,物块受到地面的摩擦力不变
C.风速由 $ 4\mathrm{m}/\mathrm{s} $ 变为 $ 6\mathrm{m}/\mathrm{s} $ 时,物块受到地面的摩擦力变大
D.风速由 $ 4\mathrm{m}/\mathrm{s} $ 变为 $ 6\mathrm{m}/\mathrm{s} $ 时,物块受到地面的摩擦力不变
答案:AD
解析:由题可知,当风速小于 $ 3\mathrm{m}/\mathrm{s} $ 时,物块静止,风对物块的推力与摩擦力平衡,所以随着风速增大,风对物块的推力增大,摩擦力增大,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;当风速大于 $ 3\mathrm{m}/\mathrm{s} $ 时,物块处于运动状态,摩擦力为滑动摩擦力,大小不变,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
5.如图所示,一木板 $ B $ 放在水平地面上,木块 $ A $ 放在 $ B $ 的上面, $ A $ 的右端通过水平轻质弹簧 $ ( $ 劲度系数 $ k=500\mathrm{N}/\mathrm{m}) $ 固定在竖直墙壁上,用大小为 $ F=28\mathrm{N} $ 的外力水平向左拉动木板 $ B $ ,使它向左匀速运动,弹簧的伸长量恒为 $ 3\mathrm{c}\mathrm{m} $ ,已知 $ A $ 、 $ B $ 的质量分别为 $ {m}_{A}=4\mathrm{k}\mathrm{g} $ 、 $ {m}_{B}=5\mathrm{k}\mathrm{g} $ , $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,求:
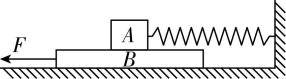
(1) 弹簧弹力 $ {F}_{弹} $ 的大小;
(2) $ B $ 对 $ A $ 的摩擦力 $ {f}_{BA} $ ;
(3) $ B $ 与地面间的动摩擦因数.
答案:(1) $ 15\mathrm{N} $
(2) $ 15\mathrm{N} $ ,方向水平向左
(3) $ \dfrac{13}{90} $
解析:(1) 由胡克定律可得 $ {F}_{弹}=kx=15\mathrm{N} $ .
(2) 由题意可知, $ A $ 相对 $ B $ 向右运动,故 $ B $ 对 $ A $ 的摩擦力方向水平向左,因弹簧的伸长量恒为 $ 3\mathrm{c}\mathrm{m} $ ,说明 $ B $ 向左匀速运动的过程中 $ A $ 对地静止,根据二力平衡,可知 $ B $ 对 $ A $ 的摩擦力大小 $ {f}_{BA}={F}_{弹}=15\mathrm{N} $ .
(3) $ B $ 向左匀速运动时,对 $ B $ 受力分析如图所示,
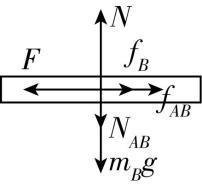
其中 $ {f}_{AB}={f}_{BA} $ , $ {N}_{AB}={m}_{A}g $ , $ {f}_{B}=\mu N=\mu ({m}_{A}g+{m}_{B}g) $ ,根据平衡条件可得 $ F={f}_{AB}+{f}_{B} $ ,解得 $ \mu =\dfrac{13}{90} $ .
6.质量为 $ m=2\mathrm{k}\mathrm{g} $ 的物体静止在水平地板上,用一轻弹簧水平推或拉该物体,已知弹簧原长 $ {l}_{0}=10\mathrm{c}\mathrm{m} $ ,劲度系数 $ k=200\mathrm{N}/\mathrm{m} $ .若拉物体,当拉着物体匀速前进时,弹簧伸长到 $ 12\mathrm{c}\mathrm{m} $ ,设最大静摩擦力等于滑动摩擦力, $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .

(1) 求物体和地板间的动摩擦因数;
(2) 若用轻弹簧水平推该物体,弹簧压缩到 $ 9\mathrm{c}\mathrm{m} $ ,则物体所受的摩擦力大小为多少?
答案:(1) 0.2
(2) $ 2\mathrm{N} $
解析:(1) 物体匀速前进,根据平衡条件可得 $ f=k({l}_{1}-{l}_{0})=200×(12-10)×{10}^{-2}\mathrm{N}=4\mathrm{N} $ ,
又 $ f=\mu mg $ ,
联立解得 $ \mu =0.2 $ .
(2) 弹簧压缩到 $ 9\mathrm{c}\mathrm{m} $ ,假设物体保持静止,物体所受的摩擦力大小为 $ f\prime =k({l}_{0}-{l}_{2})=200×(10-9)×{10}^{-2}\mathrm{N}=2\mathrm{N} < f $ ,
假设成立,故物体所受的摩擦力大小为 $ 2\mathrm{N} $ .
7.如图甲为测定金属块 $ A $ 与长木板 $ B $ 之间的动摩擦因数 $ \mu $ 的实验器材,同学们设计了以下实验步骤:
①将弹簧测力计竖直调零;
②弹簧测力计静止状态测量金属块的重力,读出弹簧测力计的示数;
③将水平调零后的弹簧测力计与金属块水平连接,置于长木板一端,测量 $ A $ 、 $ B $ 间滑动摩擦力的大小;
④运用测量数据计算动摩擦因数 $ \mu $ .

甲
(1) 步骤③中,两位同学设计了如图乙(木板固定,拉动金属块)、图丙(金属块固定,拉动木板)所示的两种方案,下列说法正确的是 .
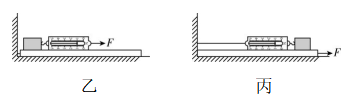
A.乙、丙两种情况都需要匀速拉动
B.乙、丙两种情况都不需要匀速拉动
C.乙需要匀速拉动,丙不需要匀速拉动
D.乙不需要匀速拉动,丙需要匀速拉动
(2) 你认为乙、丙两种方案 (填“乙”或“丙”)更合理,你选择的理由是 .
(3) 若测得金属块重力大小为 $ {F}_{1} $ ,在丙方案中弹簧测力计示数为 $ {F}_{2} $ ,则 $ A $ 、 $ B $ 间的动摩擦因数 $ \mu = $ .
答案:(1) C
(2) 丙;很难做到用弹簧测力计匀速拉动金属块,所以实验测量数值不稳定
(3) $ \dfrac{{F}_{2}}{{F}_{1}} $
解析:(1) 题图乙中金属块水平方向受到拉力与摩擦力,则要使弹簧测力计测量的数值为滑动摩擦力的数值,需要匀速拉动弹簧测力计,题图丙中拉动下面的木板,金属块始终处于静止状态,弹簧测力计测量的数值为滑动摩擦力的数值,则不需要匀速拉动木板, $ \mathrm{C} $ 正确.
(2) 对于两种方案,丙比较合理,因为很难做到用弹簧测力计匀速拉动金属块,且金属块运动中弹簧测力计不方便读数,所以实验测量数值不稳定.
(3) 由滑动摩擦力公式可知 $ f=\mu {F}_{\mathrm{N}} $ ,其中 $ f={F}_{2} $ , $ {F}_{\mathrm{N}}={F}_{1} $ ,解得 $ \mu =\dfrac{{F}_{2}}{{F}_{1}} $ .
8.如图所示的下列几种情形中,研究对象受到的摩擦力方向与运动方向相同的是( )
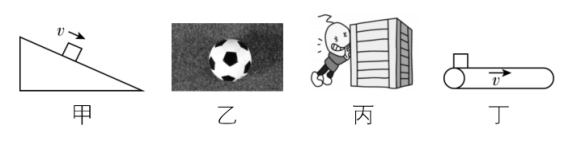
A.图甲:沿斜面匀速下滑的物块
B.图乙:在草地上滚动的足球
C.图丙:水平地面上匀速运动的木箱
D.图丁:轻放在运动的水平传送带上的物块(与传送带共速前)
答案:D
解析:沿斜面匀速下滑的物块,受到沿斜面向上的滑动摩擦力,故 $ \mathrm{A} $ 错误;在草地上滚动的足球,受到的摩擦力与运动方向相反,故 $ \mathrm{B} $ 错误;水平地面上匀速运动的木箱,受到的摩擦力与运动方向相反,故 $ \mathrm{C} $ 错误;物块轻放上运动的传送带后与传送带共速前,受到向右的摩擦力,将向右运动,摩擦力方向与运动方向相同,故 $ \mathrm{D} $ 正确.
9.如图所示,重力为 $ G $ 的物体沿竖直墙壁下滑,物体与墙壁之间的动摩擦因数为 $ \mu $ ,则物体所受摩擦力大小为( )
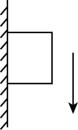
A. $ \mu G $
B.0
C. $ G $
D.无法确定
答案:B
解析:只有两物体的接触面粗糙,物体间存在压力,同时物体间存在相对运动时,物体间才存在滑动摩擦力.物体沿竖直墙壁下滑,虽然物体与墙壁接触面粗糙,但是物体与墙壁之间无挤压,即物体与墙壁之间不存在压力,故物体与墙壁之间无摩擦,故 $ \mathrm{B} $ 正确.
10.质量为 $ 20\mathrm{k}\mathrm{g} $ 的物体,在粗糙水平面上向右运动,物体与水平面间的动摩擦因数 $ \mu =0.1 $ ,同时物体还受到一个大小为 $ 10\mathrm{N} $ 、方向水平向左的拉力 $ F $ 作用,如图所示,则水平面对物体的摩擦力的大小和方向是 $ (g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2}) $ ( )
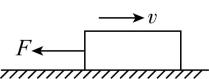
A. $ 10\mathrm{N} $ ,水平向右
B. $ 10\mathrm{N} $ ,水平向左
C. $ 20\mathrm{N} $ ,水平向右
D. $ 20\mathrm{N} $ ,水平向左
答案:D
解析:物体相对于水平面向右运动,水平面对物体的滑动摩擦力方向水平向左.物体对水平面的压力大小 $ {F}_{\mathrm{N}}=mg=200\mathrm{N} $ ,则水平面对物体的摩擦力大小 $ f=\mu {F}_{\mathrm{N}}=0.1×200\mathrm{N}=20\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.
二、刷提升
1.如图所示,物体的质量为 $ m $ ,与材质均匀的水平桌面间的动摩擦因数为 $ \mu $ ,在水平向右的推力 $ F $ 作用下匀速运动.从物体的边缘滑到桌边开始,到物体的三分之一滑离桌边为止,重力加速度为 $ g $ ,在此过程中,下列说法正确的是 ( )
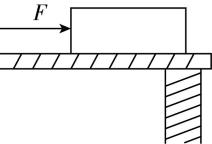
A.推力 $ F $ 因物体悬空部分越来越大而变小
B.物体所受摩擦力逐渐减小
C.推力 $ F $ 的大小始终等于 $ \mu mg $
D.因接触面积变小,动摩擦因数 $ \mu $ 会变大
答案:C
解析:当物体在桌面上匀速滑动时,物体对桌面的压力始终等于物体的重力,桌面与物体表面间的粗糙程度不变,即动摩擦因数不变,只是接触面积在逐渐减小,而接触面积的大小不影响摩擦力的大小,因此,在此过程中摩擦力是不变的, $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误;对物体受力分析,可知推力 $ F $ 的大小始终等于摩擦力 $ \mu mg $ , $ \mathrm{A} $ 错误, $ \mathrm{C} $ 正确.
2.轻弹簧一端系一方木块,竖直悬挂时弹簧伸长了 $ L $ ,将其放在水平桌面上用水平力拉弹簧使木块做匀速运动时,弹簧伸长了 $ 0.2L $ ,则木块与水平桌面间的动摩擦因数为( )
A.0.1
B.0.2
C.0.4
D.0.5
答案:B
解析:根据题意可知,当弹簧竖直悬挂木块时,有 $ mg=kL $ ,放在水平桌面上用水平力拉弹簧使木块做匀速运动时,有 $ f=\mu mg=k\cdot 0.2L $ ,联立可得 $ \mu =0.2 $ ,故选 $ \mathrm{B} $ .
3.把一小木块放在逆时针转动的水平传送带上,其右端通过一根细绳拴在墙上.小木块质量为 $ 1\mathrm{k}\mathrm{g} $ ,小木块与传送带之间的动摩擦因数为 $ 0.3 $ ,则 $ ( $ 重力加速度取 $ g=10\mathrm{m}/{\mathrm{s}}^{2}) $ ( )
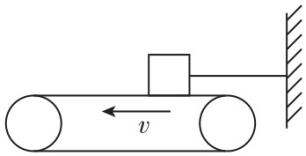
A.小木块受到的滑动摩擦力水平向右
B.小木块受到细绳的拉力大小为 $ 0.3\mathrm{N} $
C.小木块与传送带之间的滑动摩擦力大小为 $ 3\mathrm{N} $
D.剪断细绳后,小木块静止不动
答案:C
解析:传送带向左运动,小木块静止,小木块相对于传送带向右运动,所以小木块受到传送带水平向左的滑动摩擦力,故 $ \mathrm{A} $ 错误;根据滑动摩擦力公式得 $ {F}_{\mathrm{f}}=\mu mg=3\mathrm{N} $ ,故 $ \mathrm{C} $ 正确;小木块处于平衡状态,受到的细绳对它向右的拉力和传送带对它向左的滑动摩擦力大小相等,即 $ T={F}_{\mathrm{f}}=3\mathrm{N} $ ,故 $ \mathrm{B} $ 错误;剪断细绳后,小木块受到水平向左的滑动摩擦力,所以小木块向左运动,故 $ \mathrm{D} $ 错误.
4.物体 $ A $ 的重力为 $ G $ ,如图甲所示,一原长为 $ L $ 的轻弹簧将物体 $ A $ 吊起静止时,弹簧长度为 $ \dfrac{4}{3}L $ ;如图乙所示,若将物体 $ A $ 置于水平地面上,用该弹簧水平向左拉物体 $ A $ ,当物体 $ A $ 匀速运动时弹簧的长度为 $ \dfrac{17}{15}L $ .以上两种情况弹簧都没有超过弹性限度.
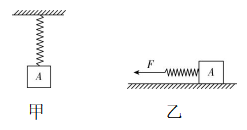
(1) 求该弹簧的劲度系数;
(2) 求物体 $ A $ 与水平地面间的动摩擦因数;
(3) 若图乙中的物体 $ A $ 向左匀速运动时弹簧的长度为 $ \dfrac{4}{3}L $ ,求此时物体 $ A $ 与水平地面间的摩擦力的大小;
(4) 若置于水平地面上的物体 $ A $ 原来静止,图乙中的弹簧长度自原长逐渐增大至 $ \dfrac{16}{15}L $ 时,求物体 $ A $ 与水平地面间的摩擦力的大小.
答案:(1) $ \dfrac{3G}{L} $
(2) 0.4
(3) $ G $
(4) $ \dfrac{1}{5}G $
解析:(1) 题图甲中弹簧将物体 $ A $ 吊起静止时,根据受力平衡可得 $ k(\dfrac{4}{3}L-L)=G $ ,解得该弹簧的劲度系数为 $ k=\dfrac{3G}{L} $ .
(2) 物体 $ A $ 水平向左匀速运动时,根据受力平衡可得 $ k(\dfrac{17}{15}L-L)=f $ ,又 $ f=\mu G $ ,联立解得物体 $ A $ 与水平地面间的动摩擦因数为 $ \mu =0.4 $ .
(3) 物体 $ A $ 向左匀速运动时,受力平衡,有 $ f\prime =k(\dfrac{4}{3}L-L)=G $ .
(4) 题图乙中的弹簧长度自原长逐渐增大至 $ \dfrac{16}{15}L $ 时,弹簧的弹力大小为 $ {F}_{弹}=k(\dfrac{16}{15}L-L)=\dfrac{1}{5}G < f=\dfrac{2}{5}G $ ,可知物体 $ A $ 仍然保持静止,此时和水平地面间的摩擦力为静摩擦力,根据受力平衡可得 $ f″={F}_{弹}=\dfrac{1}{5}G $ .
5.试卷读卡器的原理可简化成如图所示的模型,搓纸轮与答题卡之间的动摩擦因数为 $ {\mu }_{1} $ ,答题卡与答题卡之间的动摩擦因数为 $ {\mu }_{2} $ ,答题卡与底部摩擦片之间的动摩擦因数为 $ {\mu }_{3} $ ,工作时搓纸轮给第1张答题卡的压力大小为 $ F $ ,每张答题卡的质量为 $ m $ ,重力加速度为 $ g $ ,正常情况下,读卡器能做到“每次只进一张答题卡”.搓纸轮沿逆时针方向转动,带动第1张答题卡向右运动,则( )
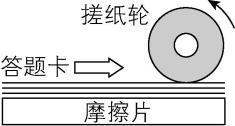
A.后一张答题卡受到前一张答题卡的摩擦力向左
B.第5张与第6张答题卡之间的摩擦力大小为 $ {\mu }_{2}(F+mg) $
C.最后一张答题卡受到摩擦片的摩擦力为零
D. $ {\mu }_{1} < {\mu }_{2} < {\mu }_{3} $
答案:B
解析:后一张答题卡相对前一张答题卡向左运动,滑动摩擦力的方向与相对运动方向相反,则后一张答题卡受到前一张答题卡的摩擦力向右,故 $ \mathrm{A} $ 错误;当第1张答题卡向右运动时,第1张答题卡对第2张答题卡的压力为 $ F+mg $ ,则第1、2张答题卡间滑动摩擦力大小为 $ f={\mu }_{2}(F+mg) $ ,此时第3张及以下的答题卡均处于静止状态,对第 $ 2\sim 5 $ 张答题卡整体进行受力分析,由平衡条件可得第6张答题卡对第5张答题卡的静摩擦力与第1张答题卡对第2张答题卡的滑动摩擦力平衡,大小为 $ {\mu }_{2}(F+mg) $ ,故 $ \mathrm{B} $ 正确;搓纸轮沿逆时针方向转动,带动答题卡向右运动的过程中,最后一张答题卡相对摩擦片有向右运动的趋势,则其受到摩擦片的摩擦力向左,故 $ \mathrm{C} $ 错误;为了保证“每次只进一张答题卡”,当最后还剩余两张答题卡时,倒数第二张答题卡向右运动,最后一张答题卡不能动,对最后一张答题卡受力分析,则有 $ {\mu }_{2}(F+mg)⩽ {\mu }_{3}(F+2mg) $ ,正常情况下 $ F\gg mg $ ,则 $ {\mu }_{2}⩽ {\mu }_{3} $ ,当剩最后一张答题卡时,需满足 $ {\mu }_{1}F > {\mu }_{3}(F+mg) $ ,则 $ {\mu }_{1} > {\mu }_{3} $ ,故 $ {\mu }_{1} > {\mu }_{3}⩾ {\mu }_{2} $ ,故 $ \mathrm{D} $ 错误.


 (多选)
(多选)