课时2 力的分解
一、刷基础
1.将力 $ F $ 进行分解,下列说法正确的是( )
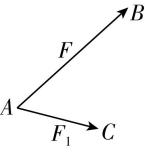
A.如图所示, $ {F}_{1} $ 是 $ F $ 的一个分力,则另一个分力 $ {F}_{2} $ 应该由 $ B $ 指向 $ C $
B.无论怎么改变分力与 $ F $ 的夹角, $ F $ 一定是最大的
C.若受力分析中对 $ F $ 进行了分解,则之后的分析中就不应再将 $ F $ 计算在内
D.若 $ F $ 与 $ {F}_{1} $ 的大小一定,另一分力 $ {F}_{2} $ 的方向一定,则 $ {F}_{2} $ 的大小有两种可能
答案:C
解析:若 $ {F}_{1} $ 是 $ F $ 的一个分力,由三角形定则可知 $ F $ 为 $ {F}_{1} $ 和 $ {F}_{2} $ 首尾相连得到的,则另一个分力 $ {F}_{2} $ 应该由 $ C $ 指向 $ B $ ,故 $ \mathrm{A} $ 错误;随着夹角的变化,合力 $ F $ 与分力的关系为 $ |{F}_{1}-{F}_{2}|⩽ F⩽ {F}_{1}+{F}_{2} $ ,则改变分力与 $ F $ 的夹角, $ F $ 不一定是最大的,故 $ \mathrm{B} $ 错误;若受力分析时对 $ F $ 进行了分解,则之后的分析中就只考虑两分力,而不应再将 $ F $ 计算在内,故 $ \mathrm{C} $ 正确;若 $ F $ 与 $ {F}_{1} $ 的大小一定,另一分力 $ {F}_{2} $ 的方向一定,则 $ {F}_{2} $ 的大小有两种可能或一种可能或无解,故 $ \mathrm{D} $ 错误.
2.家里的书桌离墙太近,某同学想将书桌向外移动一点,但她力气太小,推不动.于是,她找来两块相同的木块,搭成一个人字形架,然后往中央一站,书桌真的移动了.下列说法中正确的是( )
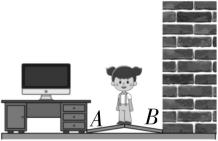 (多选)
(多选)
A.这是因为在人字形架的夹角很大的情况下,该同学的重力沿木块方向的分力很大
B.这是因为在人字形架的夹角很大的情况下,该同学的重力沿木块方向的分力很小
C.人字形架的夹角越大,越容易推动书桌
D.人字形架的夹角越大,越难推动书桌
答案:AC
解析:重力的大小和方向始终不变,分解到两木块方向时,设人字形架的夹角为 $ \theta $ ,由平衡条件有 $ 2F \cos \dfrac{\theta }{2}=G $ ,可得该同学的重力沿木块方向的分力大小为 $ F=\dfrac{G}{2 \cos \dfrac{\theta }{2}} $ ,可知人字形架的夹角越大,该同学的重力沿两木块方向的作用力越大,越容易推动书桌.故选 $ \mathrm{A} $ 、 $ \mathrm{C} $ .
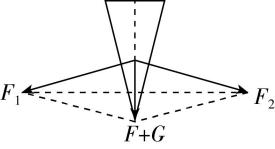
3.如图所示,斧头的纵截面是一个等腰三角形,侧面长为 $ l $ ,背宽为 $ d $ ,自身重力为 $ G $ .现用竖直向下的力 $ F $ 将斧头敲入木柴中,忽略斧头侧面与木柴间的摩擦,则斧头的侧面推压木柴的力的大小为( )

A. $ \dfrac{l}{d}(F+G) $
B. $ \dfrac{l}{d}F $
C. $ \dfrac{l}{2d}(F+G) $
D. $ \dfrac{l}{2d}F $
答案:A
解析:将力 $ (F+G) $ 分解为 $ {F}_{1} $ 、 $ {F}_{2} $ 两个分力,这两个分力分别与斧头的两个侧面垂直,如图所示,根据对称性可知,两分力 $ {F}_{1} $ 、 $ {F}_{2} $ 大小相等,则以 $ {F}_{1} $ 、 $ {F}_{2} $ 为邻边的平行四边形是一个菱形,因为菱形的对角线互相垂直且平分,根据相似三角形有 $ \dfrac{\dfrac{d}{2}}{l}=\dfrac{\dfrac{F+G}{2}}{{F}_{1}} $ ,解得 $ {F}_{1}=\dfrac{l}{d}(F+G) $ ,故选 $ \mathrm{A} $ .
4.风对帆面的作用力垂直于帆面,它能分解成两个分力:垂直于航向的分力,会被很大的水的横向阻力平衡;沿着航向的分力,提供船向前的动力.下列船帆与风的方向组合能使船沿航向方向行驶的是( )
A.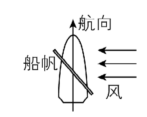
B.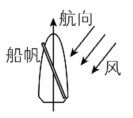
C.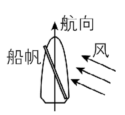
D.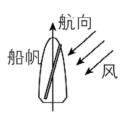
答案:D
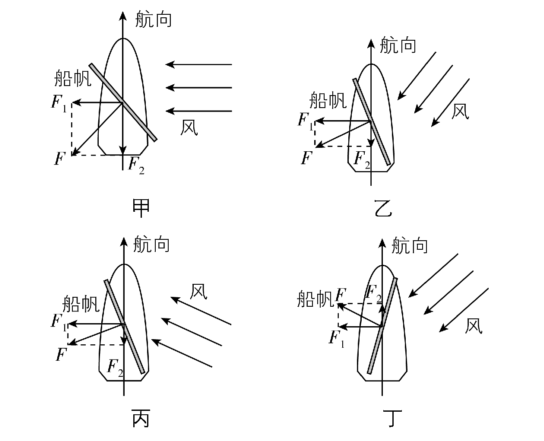
解析:图A中船帆受到风的作用力,如图甲所示,由于 $ {F}_{2} $ 方向与航向相反,故 $ \mathrm{A} $ 错误;图B中船帆受到风的作用力,如图乙所示,由于 $ {F}_{2} $ 方向与航向相反,故 $ \mathrm{B} $ 错误;图C中船帆受到风的作用力,如图丙所示,由于 $ {F}_{2} $ 方向与航向相反,故 $ \mathrm{C} $ 错误;图D中船帆受到风的作用力,如图丁所示,由于 $ {F}_{2} $ 方向与航向相同,故 $ \mathrm{D} $ 正确.
5.如图所示,固定在水平地面上的光滑斜面的倾角为 $ \theta $ ,有两个完全相同的小球分别用光滑挡板 $ A $ 、 $ B $ 挡住.挡板 $ A $ 沿竖直方向放置,斜面对球1的支持力大小为 $ {N}_{1} $ ,挡板 $ B $ 垂直于斜面放置,斜面对球2的支持力大小为 $ {N}_{2} $ ,求 $ {N}_{1}:{N}_{2} $ .
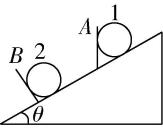
答案: $ 1:{ \cos }^{2}\theta $
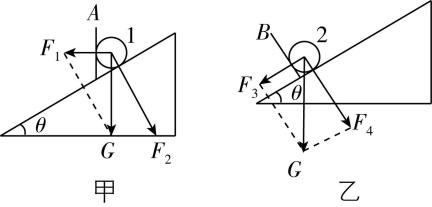
解析:把球1、2所受重力按力的作用效果分解,如图甲、乙所示.斜面对球1的支持力大小 $ {N}_{1}={F}_{2}=\dfrac{G}{ \cos \theta } $ ,斜面对球2的支持力大小 $ {N}_{2}={F}_{4}=G \cos \theta $ ,所以 $ {N}_{1}:{N}_{2}=1:{ \cos }^{2}\theta $ .
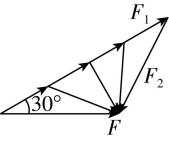
6.小明同学用两个力将一重力大小为 $ 100\mathrm{N} $ 的物体悬挂起来,力 $ {F}_{1} $ 的方向与竖直方向成 $ {30}^{\circ } $ 角,力 $ {F}_{2} $ 的大小为 $ 60\mathrm{N} $ ,则( )
A. $ {F}_{1} $ 的大小是唯一的
B. $ {F}_{2} $ 的方向是唯一的
C. $ {F}_{2} $ 有两个可能的方向
D. $ {F}_{2} $ 可取任意方向
答案:C
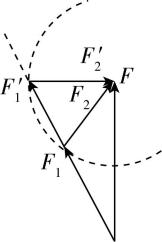
解析:如图所示,以 $ F=G=100\mathrm{N} $ 的力的“箭头”为圆心,以 $ {F}_{2} $ 的大小 $ 60\mathrm{N} $ 为半径画一个圆弧,圆弧与 $ {F}_{1} $ 所在直线有两个交点,因此 $ {F}_{2} $ 有两个可能的方向, $ {F}_{1} $ 的大小有两个可能的值.故选 $ \mathrm{C} $ .
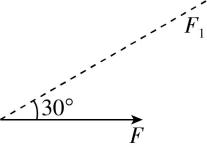
7.如图所示,将一个大小 $ F=10\mathrm{N} $ 的力分解为两个力,已知其中一个分力 $ {F}_{1} $ 的方向与 $ F $ 的夹角为 $ {30}^{\circ } $ ,另一个分力为 $ {F}_{2} $ ,下列说法正确的是( )
 (多选)
(多选)
A. $ {F}_{2} $ 的大小不可能小于 $ 5\mathrm{N} $
B. $ {F}_{1} $ 的大小存在最大值
C. $ {F}_{2} $ 的方向与 $ {F}_{1} $ 垂直时, $ {F}_{2} $ 最小
D. $ {F}_{1} $ 的大小不可能小于 $ 5\mathrm{N} $
答案:AC
解析: $ {F}_{1} $ 、 $ {F}_{2} $ 如图所示,根据三角形定则,当 $ {F}_{2} $ 与 $ {F}_{1} $ 垂直时, $ {F}_{2} $ 最小, $ {F}_{2} $ 的最小值为 $ {F}_{ \min }=F \sin {30}^{\circ }=5\mathrm{N} $ ,故 $ {F}_{2} $ 的大小不可能小于 $ 5\mathrm{N} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确;只确定 $ {F}_{1} $ 的方向时, $ {F}_{2} $ 的长度不存在最大值,所以 $ {F}_{1} $ 的大小也不存在最大值, $ {F}_{1} $ 的大小范围为 $ 0\mathrm{~}\mathrm{\infty } $ ,故 $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误.
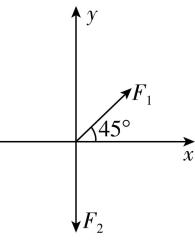
8.如图所示,一物体受到两个力作用,其中 $ {F}_{1}=10\sqrt{2}\mathrm{N} $ , $ {F}_{2}=20\mathrm{N} $ , $ {F}_{1} $ 与 $ x $ 轴正方向夹角为 $ {45}^{\circ } $ , $ {F}_{2} $ 沿 $ y $ 轴负方向,则这两个力的合力大小与方向分别为( )
A. $ 20\mathrm{N} $ ,方向沿 $ x $ 轴正方向
B. $ 20\mathrm{N} $ ,方向沿 $ y $ 轴正方向
C. $ 10\sqrt{2}\mathrm{N} $ ,方向与 $ x $ 轴正方向夹角为 $ {45}^{\circ } $
D. $ 10\sqrt{2}\mathrm{N} $ ,方向与 $ x $ 轴负方向夹角为 $ {45}^{\circ } $
答案:C
解析:正交分解 $ {F}_{1} $ , $ x $ 轴方向的合力为 $ {F}_{x}={F}_{1} \cos {45}^{\circ }=10\mathrm{N} $ ,沿 $ x $ 轴正方向, $ y $ 轴方向的合力为 $ {F}_{y}={F}_{2}-{F}_{1} \sin {45}^{\circ }=10\mathrm{N} $ ,沿 $ y $ 轴负方向.故这两个力的合力大小 $ F=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}=10\sqrt{2}\mathrm{N} $ ,方向与 $ x $ 轴正方向夹角为 $ {45}^{\circ } $ .故选 $ \mathrm{C} $ .
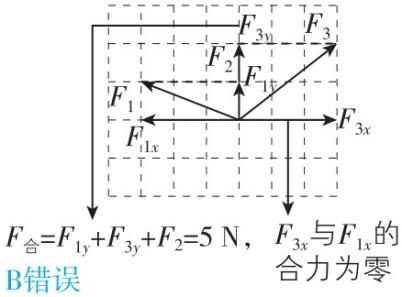
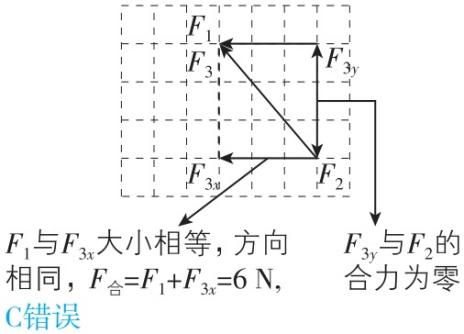
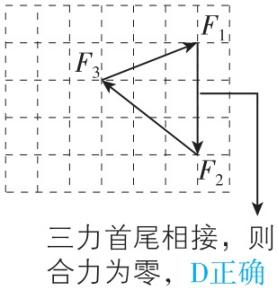
9.某物体同时受到同一个平面内的三个力的作用,在如图所示的四种情况中(坐标纸中每格边长表示 $ 1\mathrm{N} $ 大小的力),关于物体受到的合力大小的说法正确的是( )
 (多选)
(多选)
A.甲图中物体所受的合力大小等于 $ 5\mathrm{N} $
B.乙图中物体所受的合力大小等于 $ 2\mathrm{N} $
C.丙图中物体所受的合力大小等于0
D.丁图中物体所受的合力大小等于0
答案:AD
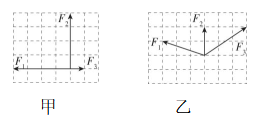
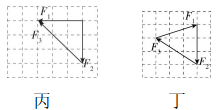
10.几种矢量运算过程如图所示,线段的长短代表矢量的大小,箭头的指向代表矢量的方向,下列说法正确的是( )

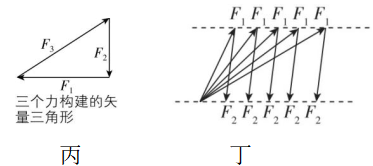
A.甲图说明物体做减速运动,速度的变化量由初速度的箭头端指向末速度的箭头端
B.乙图说明两个力的合力由一个力的箭头端指向另一个力的箭尾端
C.丙图的三个力的合力一定为零
D.丁图说明两个力 $ {F}_{1} $ 、 $ {F}_{2} $ 的合力的大小、方向都改变
答案:C
解析:题图甲说明物体做加速运动,速度的变化量由初速度的箭头端指向末速度的箭头端, $ \mathrm{A} $ 错误;题图乙说明两分力的合力由一个分力的箭尾端指向另一个分力的箭头端, $ \mathrm{B} $ 错误;题图丙的三个力的矢量线段首尾相连,组成封闭的三角形,三个力的合力一定为零, $ \mathrm{C} $ 正确;题图丁的两个力矢量线段首尾相连,其合力由 $ {F}_{1} $ 的箭尾端指向 $ {F}_{2} $ 的箭头端,合力的方向向右,都在同一条直线上,即合力的大小改变,方向不变, $ \mathrm{D} $ 错误.
11.如图所示,把光滑斜面上物体的重力 $ mg $ 分解为 $ {F}_{1} $ 、 $ {F}_{2} $ 两个力,下列说法正确的是( )
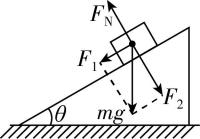
A. $ {F}_{1} $ 是斜面作用在物体上使物体下滑的力, $ {F}_{2} $ 是物体对斜面的压力
B.物体受到 $ mg $ 、 $ {F}_{\mathrm{N}} $ 、 $ {F}_{1} $ 、 $ {F}_{2} $ 四个力作用
C. $ {F}_{\mathrm{N}} $ 和 $ {F}_{2} $ 是作用力和反作用力
D.力 $ {F}_{\mathrm{N}} $ 、 $ {F}_{1} $ 、 $ {F}_{2} $ 三个力的作用效果和 $ mg $ 与 $ {F}_{\mathrm{N}} $ 两个力的作用效果相同
答案:D
解析: $ {F}_{1} $ 、 $ {F}_{2} $ 两个力是重力的分力,不是物体实际受到的力, $ {F}_{2} $ 的作用点在物体上,不在斜面上,所以不是物体对斜面的压力,故 $ \mathrm{A} $ 错误;物体受到 $ mg $ 、 $ {F}_{\mathrm{N}} $ 两个力的作用, $ {F}_{1} $ 、 $ {F}_{2} $ 两个力是重力的分力,不能与重力同时作用在物体上,故 $ \mathrm{B} $ 错误; $ {F}_{\mathrm{N}} $ 和 $ {F}_{2} $ 大小相等、方向相反,都作用在物体上,是一对平衡力,不是作用力和反作用力,故 $ \mathrm{C} $ 错误;由于 $ {F}_{1} $ 、 $ {F}_{2} $ 共同作用的效果与重力作用的效果相同,所以 $ {F}_{\mathrm{N}} $ 、 $ {F}_{1} $ 、 $ {F}_{2} $ 三个力的作用效果和 $ mg $ 、 $ {F}_{\mathrm{N}} $ 两个力的作用效果相同,故 $ \mathrm{D} $ 正确.
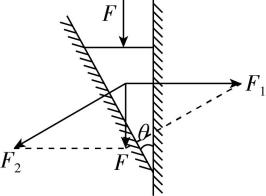
12.榫卯结构是中国传统建筑、家具和其他木制器具的主要结构方式.如图所示为榫眼的凿削操作的截面图,凿子尖端夹角为 $ \theta $ ,在凿子顶部施加竖直向下的力 $ F $ 时,其竖直面和侧面对两侧木头的压力分别为 $ {F}_{1} $ 和 $ {F}_{2} $ ,不计凿子的重力及摩擦力,下列说法正确的是( )
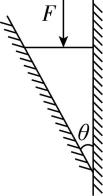
A. $ {F}_{1}={F}_{2} \cos \theta $
B. $ {F}_{2}={F}_{1} \cos \theta $
C.夹角 $ \theta $ 越小, $ {F}_{1} $ 越大, $ {F}_{2} $ 越小
D.夹角 $ \theta $ 越大,凿子越容易凿入木头
答案:A
解析:将力 $ F $ 按照作用效果分解为 $ {F}_{1} $ 、 $ {F}_{2} $ ,如图所示,由图可知 $ {F}_{1}={F}_{2} \cos \theta $ , $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误.由几何关系有 $ {F}_{2}=\dfrac{F}{ \sin \theta } $ , $ {F}_{1}=\dfrac{F}{ \tan \theta } $ ,可知力 $ F $ 一定时,夹角 $ \theta $ 越小, $ {F}_{1} $ 、 $ {F}_{2} $ 均越大;夹角 $ \theta $ 越大, $ {F}_{1} $ 、 $ {F}_{2} $ 均越小,越不容易凿入木头, $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
二、刷提升
1.力的合成和分解在生产和生活中有着重要的作用,下列说法中正确的是( )
A.高大的桥要建很长的引桥,减小斜面倾角,是为了减小汽车行驶过程中重力沿斜面的分力和摩擦力
B.刀刃前部和后部厚薄不匀,仅是为了外形美观,跟使用功能无关
C.运动员做引体向上(缓慢上升)动作时,双臂张开很大的角度时要比双臂平行时费力(即需要更大的力)
D.将车与树用水平张紧的钢索相连,在钢索中点垂直汽车与树连线方向,必须施加一个大于钢索拉力的力才可能把陷入泥沼的车拉出
答案:C
解析:高大的桥要建很长的引桥,减小斜面倾角,是为了减小汽车行驶过程中重力沿斜面的分力,增大重力垂直于斜面的分力,从而增大摩擦力,故 $ \mathrm{A} $ 错误;对刀施加力时,有 $ F=2{F}_{1} \cos \theta $ ,刀刃越薄,则 $ \theta $ 越大, $ \cos \theta $ 越小, $ {F}_{1} $ 越大,更容易切开食物,所以刀刃前部和后部厚薄不匀,跟使用功能有关,故 $ \mathrm{B} $ 错误;运动员做引体向上(缓慢上升)动作时,有 $ mg=2F \cos \theta $ ,双臂张开很大的角度时,即 $ \theta $ 变大, $ \cos \theta $ 变小, $ F $ 变大,即比双臂平行时费力(即需要更大的力),故 $ \mathrm{C} $ 正确;将车与树用水平张紧的钢索相连,在钢索中点垂直汽车与树连线方向施加一个力,此时有 $ F=2{F}_{1} \cos \theta $ ,当 $ \theta $ 较大时, $ \cos \theta $ 较小, $ F $ 小于 $ {F}_{1} $ ,即施加的作用力小于钢索的拉力,故 $ \mathrm{D} $ 错误.
2.如图所示,两细杆间距离相同、与水平地面所成的角度均为 $ \alpha $ ,一质量为 $ m $ 的小球从装置顶端由静止释放,离开细杆前的运动可视为匀加速直线运动,重力加速度为 $ g $ .当两杆对小球的支持力的夹角为 $ 2\theta $ 时,此时每根杆的支持力大小为( )
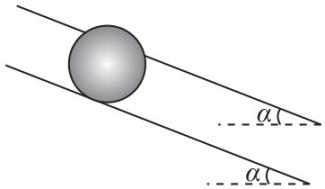
A. $ \dfrac{mg \sin \alpha }{2 \cos \theta } $
B. $ \dfrac{mg \cos \alpha }{2 \sin \theta } $
C. $ \dfrac{mg \cos \alpha }{2 \cos \theta } $
D. $ \dfrac{mg \sin \alpha }{2 \sin \theta } $
答案:C
解析:设两细杆对小球支持力的合力为 $ {F}_{\mathrm{N}} $ ,可知 $ {F}_{\mathrm{N}}=mg \cos \alpha $ ,设每根杆的支持力大小为 $ F $ ,由平行四边形定则可得 $ 2F \cos \theta ={F}_{\mathrm{N}} $ ,解得 $ F=\dfrac{mg \cos \alpha }{2 \cos \theta } $ ,故选 $ \mathrm{C} $ .
3.如图所示,倾角为 $ \theta $ 的光滑斜面长和宽均为 $ l $ ,一质量为 $ m $ 的物体由斜面左上方顶点 $ P $ 静止释放,若要求物体沿 $ PQ $ 连线滑到 $ Q $ 点,已知重力加速度为 $ g $ .则在斜面上,可以对物体施加的作用力大小不可能为( )
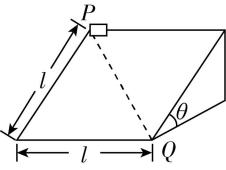
A. $ mg \sin \theta $
B. $ mg $
C. $ \dfrac{\sqrt{3}}{2}mg \sin \theta $
D. $ \dfrac{\sqrt{3}}{3}mg \sin \theta $
答案:D
解析:物体在斜面上受到重力、支持力和外力,在三力作用下沿对角线做直线运动.将重力沿斜面向下和垂直于斜面方向正交分解,沿斜面方向的合力与 $ PQ $ 共线,根据矢量三角形可知,当外力垂直于 $ PQ $ 时,外力最小,所施加的外力的最小值为 $ {F}_{ \min }=mg \sin \theta \sin {45}^{\circ }=\dfrac{\sqrt{2}}{2}mg \sin \theta $ ,所以对物体施加的作用力大小应满足 $ F⩾ \dfrac{\sqrt{2}}{2}mg \sin \theta $ ,故选 $ \mathrm{D} $ .
4.汽车发生爆胎后,需要用千斤顶抬起汽车后更换轮胎.当摇动把手时,水平面上的千斤顶的两臂(长度相等)靠拢,顶起汽车.图(a)、 $ (\mathrm{b}) $ 为汽车内常备的两种类型的千斤顶,一种是“ $ \mathrm{Y} $ ”形,另一种是“菱形”,摇动手柄,使螺旋杆转动, $ A $ 、 $ B $ 间距离发生改变,从而实现重物的升降.若重物的重力为 $ G $ , $ AB $ 与 $ AC $ 间的夹角为 $ \theta $ ,螺旋杆保持水平,不计杆自身重力,求图(a)、 $ (\mathrm{b}) $ 两种千斤顶螺旋杆的拉力大小之比.
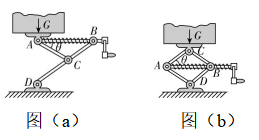
解析:“ $ \mathrm{Y} $ ”形千斤顶的 $ A $ 点受力分析如图甲所示,将压力 $ T $ 分解为拉螺旋杆的力 $ {F}_{1} $ 和压斜杆的力 $ F $ ,作出平行四边形,可知 $ T=G $ , $ {F}_{1}=\dfrac{G}{ \tan \theta } $ ,对“菱形”千斤顶的 $ A $ 点和 $ C $ 点受力分析如图乙所示,根据力的实际作用效果,首先将压力 $ T $ 分解为两个等大的力 $ F\prime $ ,有 $ F\prime =\dfrac{G}{2 \sin \theta } $ , $ F\prime $ 作用在 $ A $ 点,又可以分解为拉螺旋杆的力 $ F{\prime }_{1} $ 和压斜杆的力 $ {F}_{2} $ ,由于四边形 $ ACBD $ 是一个菱形,根据力的三角形与几何三角形相似可得 $ {F}_{2}=F\prime $ ,在 $ A $ 处可得 $ F{\prime }_{1}=2F\prime \cos \theta $ ,所以 $ F{\prime }_{1}=\dfrac{G}{2 \sin \theta }\cdot 2 \cos \theta =\dfrac{G}{ \tan \theta } $ ,则题图(a)、 $ (\mathrm{b}) $ 两种千斤顶螺旋杆的拉力大小之比为 $ 1:1 $ .
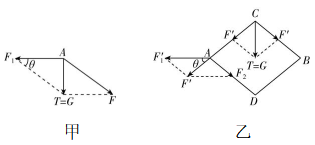
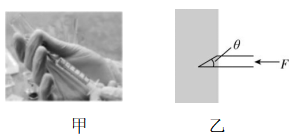
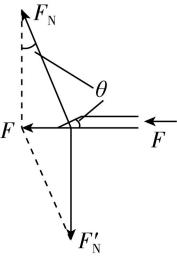
5.在药物使用时应用到很多物理知识.如图甲、乙分别是用注射器取药的情景和针尖刺入瓶塞的示意图.针尖的顶角 $ \theta $ 很小,医生沿着注射器施加一个较小的力 $ F $ ,针尖会对瓶塞产生很大的推力,现只分析图乙的针尖倾斜侧面与直侧面对瓶塞产生的两个推力,则( )
 (多选)
(多选)
A.针尖在两个侧面上对瓶塞的两个推力是等大的
B.针尖在倾斜侧面上对瓶塞的推力比直侧面的推力大
C.若 $ F $ 一定,增大 $ \theta $ ,直侧面推力减小
D.若 $ \theta $ 一定,增大 $ F $ ,直侧面与倾斜侧面推力之比增大
答案:BC
解析:将力 $ F $ 沿垂直于两个侧面的方向分解,如图所示,则 $ \dfrac{F{\prime }_{\mathrm{N}}}{{F}_{\mathrm{N}}}= \cos \theta $ ,若 $ \theta $ 一定,增大 $ F $ ,直侧面与倾斜侧面推力之比不变,则 $ F{\prime }_{\mathrm{N}} < {F}_{\mathrm{N}} $ ,即针尖在倾斜侧面上对瓶塞的推力比直侧面的推力大,故 $ \mathrm{A} $ 、 $ \mathrm{D} $ 错误, $ \mathrm{B} $ 正确;分析可知 $ \dfrac{F}{F{\prime }_{\mathrm{N}}}= \tan \theta $ ,解得 $ F{\prime }_{\mathrm{N}}=\dfrac{F}{ \tan \theta } $ ,若 $ F $ 一定,增大 $ \theta $ ,则直侧面推力 $ F{\prime }_{\mathrm{N}} $ 减小,故 $ \mathrm{C} $ 正确.

 (多选)
(多选)








 (多选)
(多选)


 (多选)
(多选)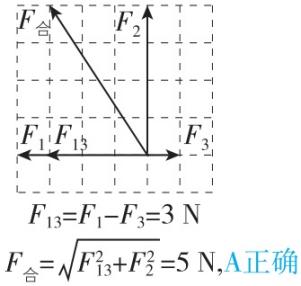








 (多选)
(多选)