实验3 探究两个互成角度的力的合成规律
一、刷题型
1.在“探究两个互成角度的力的合成规律”实验中,如图所示,用 $ A $ 、 $ B $ 两只弹簧测力计把橡皮条上的结点拉到某一位置 $ O $ ,这时两绳套 $ AO $ 、 $ BO $ 的夹角小于 $ {90}^{\circ } $ ,现在保持弹簧测力计 $ A $ 的示数不变而改变其拉力方向使 $ \alpha $ 角变小,那么要使结点仍在位置 $ O $ ,就应该调整弹簧测力计 $ B $ 的拉力大小及 $ \beta $ 角,下列调整方法中可行的是( )

A.增大 $ B $ 的拉力,增大 $ \beta $ 角
B.增大 $ B $ 的拉力, $ \beta $ 角不变
C.减小 $ B $ 的拉力,减小 $ \beta $ 角
D. $ B $ 的拉力大小不变,增大 $ \beta $ 角
答案:AB
解析: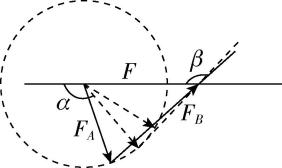
由题意可知,保持 $ O $ 点位置不动,即合力大小、方向均不变,弹簧测力计 $ A $ 的示数不变,只要符合该条件而且能够作出力的平行四边形即可;保持长度不变将 $ {F}_{A} $ 绕橡皮条上的力 $ F $ 端点转动形成一个圆弧, $ {F}_{B} $ 的一个端点不动,另一个端点在圆弧上滑动即可看出结果,如图所示.由于两绳套 $ AO $ 、 $ BO $ 的夹角小于 $ {90}^{\circ } $ ,在力的三角形中, $ {F}_{A} $ 、 $ {F}_{B} $ 的顶角为钝角,当 $ {F}_{A} $ 顺时针转动时, $ {F}_{A} $ 、 $ {F}_{B} $ 的顶角先逐渐减小为直角后减小为锐角,由图可知,这个过程中 $ {F}_{B} $ 一直增大,但 $ \beta $ 角先减小后增大,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
2.某实验小组探究两个互成角度的力的合成规律.如图甲所示,橡皮条的一端固定,另一端挂有轻质小圆环,橡皮条的长度为 $ GE $ .在图乙中,用两个弹簧测力计共同拉动拴在小圆环上的两条细绳,小圆环受到拉力 $ {F}_{1} $ 、 $ {F}_{2} $ 的共同作用,静止于 $ O $ 点,记录 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小和方向.撤去 $ {F}_{1} $ 、 $ {F}_{2} $ ,改用一个力 $ F $ 单独拉住小圆环,保证与 $ {F}_{1} $ 、 $ {F}_{2} $ 共同作用的效果是相同的,记录力 $ F $ 的大小和方向,利用图示法画出力 $ F $ 、 $ {F}_{1} $ 、 $ {F}_{2} $ ,探究三者的关系.
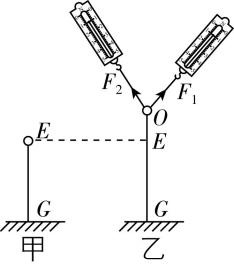
(1) 本实验采用的实验方法主要是 (填“控制变量法”或“等效替代法”).
(2) 请简述实验中如何保证“力 $ F $ 单独作用时,与 $ {F}_{1} $ 、 $ {F}_{2} $ 共同作用的效果是相同的”: .
(3) 下列操作有利于减小实验误差的是 (填字母代号).
A.拴在小圆环上的两条细绳必须等长
B.在记录力的方向时,标记同一细绳方向的两点要远些
C.用两弹簧测力计同时拉小圆环时,两条细绳之间的夹角必须取 $ {90}^{\circ } $
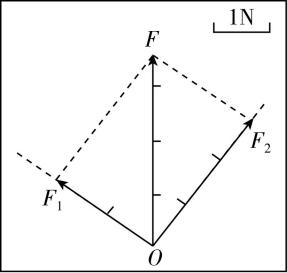
(4) 某次实验记录了 $ {F}_{1} $ 和 $ {F}_{2} $ 的方向如图丙中虚线所示, $ {F}_{1} $ 和 $ {F}_{2} $ 的大小分别为 $ 2.0\mathrm{N} $ 和 $ 3.0\mathrm{N} $ ,图中已经画出了 $ F $ 的大小和方向.请根据图中给出的力的标度,完成力 $ {F}_{1} $ 、 $ {F}_{2} $ 的图示.

丙
答案:(1) 等效替代法
(2) 实验中力 $ F $ 单独作用时,与 $ {F}_{1} $ 、 $ {F}_{2} $ 共同作用时都使小圆环静止于 $ O $ 点
(3) B
(4) 见解析
解析:(1) 合力与分力作用效果相同,所以本实验采用的实验方法主要是等效替代法.
(2) 实验中力 $ F $ 单独作用时,与 $ {F}_{1} $ 、 $ {F}_{2} $ 共同作用时都使小圆环静止于 $ O $ 点,以此保证力 $ F $ 单独作用时,与 $ {F}_{1} $ 、 $ {F}_{2} $ 共同作用的效果是相同的.
(3) 拴在小圆环上的两条细绳不一定必须等长,但是适当长一些有利于减小在确定力的方向时的误差,故 $ \mathrm{A} $ 错误;在记录力的方向时,标记同一细绳方向的两点要远些,有利于减小在确定力的方向时的误差,故 $ \mathrm{B} $ 正确;用两弹簧测力计同时拉小圆环时,两条细绳之间的夹角不一定必须取 $ {90}^{\circ } $ ,故 $ \mathrm{C} $ 错误.
(4) 根据力的标度,作出力的图示如图.
3.小明在家中用一根轻弹簧、水瓶(含水)、细绳、图钉和贴在墙上的白纸等物品,验证力的平行四边形定则.实验步骤如下:
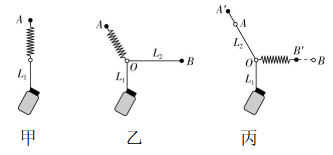
$ (\mathrm{i}) $ 先用图钉 $ A $ 将弹簧一端固定在白纸上,弹簧另一端通过细绳 $ {L}_{1} $ 悬挂水瓶(与墙、纸无摩擦),如图甲所示;
$ (\mathrm{i}\mathrm{i}) $ 将另一细绳 $ {L}_{2} $ 拴于细绳 $ {L}_{1} $ 上 $ O $ 点,并将细绳 $ {L}_{2} $ 水平拉直后用图钉 $ B $ 固定,在白纸上记下 $ A $ 、 $ B $ 、 $ O $ 的位置,如图乙所示;
$ (\mathrm{i}\mathrm{i}\mathrm{i}) $ 在保证 $ O $ 点位置不变的情况下,交换弹簧与细绳 $ {L}_{2} $ 的位置,使其方向与 $ (\mathrm{i}\mathrm{i}) $ 中对应方向平行,如图丙所示;
$ (\mathrm{i}\mathrm{v}) $ 按照上述方法改变弹簧与细绳 $ {L}_{2} $ 的夹角,重复测量多次.
(1) 对于本实验,下列说法或操作正确的是 ;(填选项前的字母)
A.还需要用天平测出水瓶(含水)的质量
B.还需要测量弹簧的原长以及图甲、乙、丙中弹簧的长度
C.为了保证实验结果尽可能准确,弹簧与细绳 $ {L}_{2} $ 的夹角应该越大越好
D.步骤 $ (\mathrm{i}\mathrm{v}) $ 中每次重复实验时,都应保证 $ O $ 点位置与第一次实验记录的位置一致
(2) 小明在进行步骤 $ (\mathrm{i}\mathrm{i}\mathrm{i}) $ 时由于粗心将水瓶中的水洒落了少许,但弹簧和细绳 $ {L}_{2} $ 的方向都与 $ (\mathrm{i}\mathrm{i}) $ 中平行, $ O $ 点位置也与 $ (\mathrm{i}\mathrm{i}) $ 中重合,这一操作 (填“会”或“不会”)造成误差.
解析:(1) 根据实验原理可知,题图甲可测量合力,题图乙、丙测量分力,结合胡克定律可知,还需要测量弹簧的原长以及题图甲、乙、丙中弹簧的长度,以便测量三个力的大小,不需要用天平测量水瓶(含水)的质量,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;为了保证实验结果尽可能准确,弹簧与细绳 $ {L}_{2} $ 的夹角适当即可,故 $ \mathrm{C} $ 错误;步骤 $ (\mathrm{i}\mathrm{v}) $ 中每次重复实验时,不需要保证 $ O $ 点位置与第一次实验记录的位置一致,从而使实验更具有普遍性,故 $ \mathrm{D} $ 错误.
(2) 水瓶中的水洒落了少许,虽然弹簧和细绳 $ {L}_{2} $ 的方向都与 $ (\mathrm{i}\mathrm{i}) $ 中平行, $ O $ 点位置也与 $ (\mathrm{i}\mathrm{i}) $ 中重合,但水瓶的重力减小,会导致弹簧弹力变小,从而造成实验误差.
4.某同学尝试做验证力的平行四边形定则的实验.他找来了定滑轮、细线和3个质量不同的苹果,3个苹果的质量分别为 $ {m}_{1} $ 、 $ {m}_{2} $ 、 $ {m}_{3} $ ,且 $ {m}_{1} < {m}_{2} < {m}_{3} $ ,按如下的步骤进行实验:
A.在墙上贴一张白纸用来记录细线的方向;
B.将定滑轮固定,用细线 $ a $ 、 $ b $ 、 $ c $ 把苹果系好,并绕过定滑轮竖直悬挂;
C.苹果保持静止状态时,记下结点位置以及3根细线的方向;
D.根据苹果的重力在白纸上按一定的标度作出力的图示.
若某次实验时,细线的方向如图所示,回答以下问题.
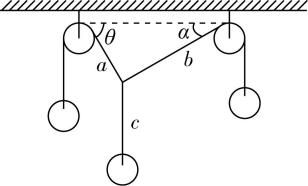
(1) 若 $ \theta ={60}^{\circ } $ , $ \alpha ={30}^{\circ } $ ,则最右侧的苹果质量为 (填“ $ {m}_{1} $ ”“ $ {m}_{2} $ ”或“ $ {m}_{3} $ ”).
(2) 要使三个苹果能够保持静止,细线 $ c $ 悬挂苹果的质量 $ {m}_{3} $ 的取值范围是 (用 $ {m}_{1} $ 、 $ {m}_{2} $ 表示).
(3) 在白纸上按一定标度作出力的图示,若细线 $ a $ 、 $ b $ 、 $ c $ 的拉力分别用 $ {F}_{a} $ 、 $ {F}_{b} $ 、 $ {F}_{c} $ 表示,根据力的平行四边形定则作出 $ {F}_{a} $ 和 $ {F}_{b} $ 的合力 $ F $ ,则一定在竖直方向的是 .
A. $ {F}_{a} $ B. $ {F}_{b} $ C. $ F $ D. $ {F}_{c} $
答案:(1) $ {m}_{1} $
(2) $ {m}_{2}-{m}_{1}⩽ {m}_{3}⩽ {m}_{1}+{m}_{2} $
(3) D
解析:(1)对结点受力分析,如图所示.三个苹果均处于静止状态,根据平衡条件可得 $ {F}_{1}={F}_{2} \sin \theta $ , $ {F}_{3}={F}_{2} \sin \alpha $ ,所以 $ {F}_{3} $ 最小,则最右侧的苹果质量最小,最右侧的苹果质量为 $ {m}_{1} $ ,中间的苹果质量最大,为 $ {m}_{3} $ ,最左侧的苹果质量为 $ {m}_{2} $ .

(2) 根据第(1)问的分析,结合合力与分力的大小关系可知, $ {m}_{2}-{m}_{1}⩽ {m}_{3}⩽ {m}_{1}+{m}_{2} $ .
(3) $ F $ 是用平行四边形定则得到的理论值,根据平衡条件可知 $ {F}_{a} $ 和 $ {F}_{b} $ 的合力 $ F $ 与 $ {F}_{c} $ 是一对平衡力,而 $ {F}_{c} $ 是实际值,方向一定是竖直向下的,由于存在误差, $ F $ 的方向可能不是竖直向上.故选 $ \mathrm{D} $ .
5.某同学设计了实验来验证力的平行四边形定则,实验步骤如下:①用天平测得物块 $ A $ 的质量为 $ m $ .②如图甲,两根竖直杆相距为 $ D $ ,用长为 $ L $ 的不可伸长的轻绳,穿过光滑的轻质动滑轮,动滑轮下端连接物体 $ A $ ,轻绳两端分别固定在杆上 $ P $ 、 $ Q $ 两点,在轻绳的左端连接力传感器,力传感器的重力忽略不计.改变物块 $ A $ 的质量 $ m $ ,记录力传感器的示数 $ F $ ,重力加速度为 $ g $ .

(1) 要验证力的平行四边形定则,力传感器的示数 $ F $ 与物块 $ A $ 的质量 $ m $ 应满足关系式 (用题中给出的物理量表示).
(2) 轻绳的 $ Q $ 端沿杆向上移动到 $ Q\prime $ ,力传感器的示数 (填“变大”“变小”或“不变”).
(3) 某同学改变物块 $ A $ 的质量,作 $ F-m $ 的图像,如图乙,图像的斜率为 $ k $ ,但是他忘记了记录间距 $ D $ 的大小, (填“可以”或“不可以”)利用图乙和已知物理量求出 $ D(L $ , $ k $ , $ g $ 已知 $ ) $ .
答案:(1) $ F=\dfrac{mgL}{2\sqrt{{L}^{2}-{D}^{2}}} $
(2) 不变
(3) 可以
解析:(1)如图所示,设滑轮处为 $ O $ 点, $ PO $ 段绳长为 $ {l}_{1} $ ,设 $ QO $ 段绳长为 $ {l}_{2} $ , $ PO $ 和 $ QO $ 与竖直方向的夹角为 $ \theta $ .
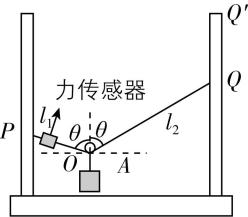
由几何关系可知 $ {l}_{1} \sin \theta +{l}_{2} \sin \theta =D $ ,又 $ {l}_{1}+{l}_{2}=L $ ,可得 $ \sin \theta =\dfrac{D}{L} $ ,由平衡条件可得 $ 2F \cos \theta =mg $ ,又 $ { \sin }^{2}\theta +{ \cos }^{2}\theta =1 $ ,联立解得 $ F=\dfrac{mgL}{2\sqrt{{L}^{2}-{D}^{2}}} $ .
(2) 由(1)分析可知,轻绳的 $ Q $ 端沿杆向上移动到 $ Q\prime $ , $ L $ 不变, $ D $ 不变,则力传感器的示数不变.
(3) 由(1)可知 $ F=\dfrac{mgL}{2\sqrt{{L}^{2}-{D}^{2}}} $ , $ F-m $ 的图像斜率为 $ k $ ,则 $ k=\dfrac{gL}{2\sqrt{{L}^{2}-{D}^{2}}} $ ,解得 $ D=\dfrac{\sqrt{4{k}^{2}-{g}^{2}}}{2k}L $ ,可利用题图乙和已知物理量求出 $ D $ .









