1．用轻质细线把两个质量未知的小球悬挂起来，如图所示.现对小球 $ a $ 持续施加一个水平向左的恒力，并对小球 $ b $ 持续施加一个水平向右同样大小的恒力，最后达到平衡状态.下列选项中表示平衡状态的图可能是（ ）
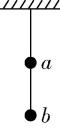
A．
B．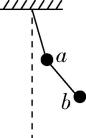
C．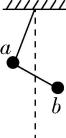
D．
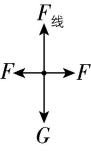
将两球和两球之间的细线看成一个整体,对整体进行受力分析如图所示,整体达到平衡状态,根据平衡条件可知整体受到小球 $ a $ 上方的细线的拉力 $ {F}_{线} $ 的大小等于小球 $ a $ 、 $ b $ 的重力大小之和,方向沿竖直方向,故小球 $ a $ 上方的细线必定沿竖直方向, $ \mathrm{A} $ 正确.
2．某体育场看台的风雨棚是钢架结构的，两侧倾斜钢柱用固定在其顶端的钢索拉住，下端用铰链与水平地面连接，钢索上有许多竖直短钢棒支撑棚顶，整个系统左右对称，结构简化图如图所示.假设钢柱与水平地面所夹锐角为 $ {60}^{\circ } $ ，钢索上端与钢柱的夹角为 $ {30}^{\circ } $ ，钢索、短钢棒及棚顶的总质量为 $ 2m $ ，重力加速度为 $ g $ ，则钢柱对钢索拉力的大小为（ ）
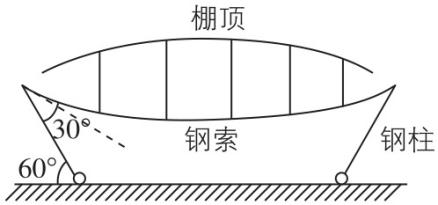
A． $ \dfrac{1}{2}mg $
B． $ 2mg $
C． $ \sqrt{3}mg $
D． $ mg $
钢索、短钢棒及棚顶作为一个整体受到三个力作用,整体重力为 $ 2mg $ ,两侧钢柱对钢索拉力大小均为 $ F $ ,根据受力平衡可得 $ 2F \sin ({60}^{\circ }-{30}^{\circ })=2mg $ ,解得 $ F=2mg $ ,故 $ \mathrm{B} $ 正确.
3．春节期间人们都喜欢在阳台上挂一些灯笼来作为喜庆的象征.如图所示，由四根等长的轻质细绳悬挂起三个质量相等的灯笼1、2、3，中间的两根细绳 $ BC $ 和 $ CD $ 之间的夹角 $ \theta ={120}^{\circ } $ ，则下列选项中正确的是（ ）
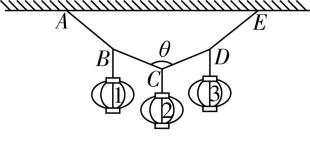
A． $ AB $ 与竖直方向的夹角为 $ {60}^{\circ } $
B． $ AB $ 的拉力为单个灯笼重力的2倍
C．绳 $ AB $ 与绳 $ BC $ 的弹力大小之比为 $ 2:1 $
D．绳 $ AB $ 与绳 $ BC $ 的弹力大小之比为 $ \sqrt{3}:1 $
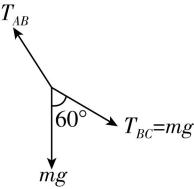
对灯笼2受力分析可知 $ {T}_{BC}={T}_{CD}=\dfrac{mg}{2 \cos {60}^{\circ }}=mg $ ,对灯笼1受力分析如图所示,根据平行四边形定则得 $ \dfrac{{T}_{AB}}{2 \cos {30}^{\circ }}=mg $ ,解得 $ {T}_{AB}=\sqrt{3}mg $ ,且 $ {T}_{AB} $ 的反向延长线过 $ {T}_{BC} $ 和灯笼1重力夹角的角平分线,故 $ AB $ 与竖直方向夹角为 $ {30}^{\circ } $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误；绳 $ AB $ 与绳 $ BC $ 的弹力大小之比为 $ \dfrac{{T}_{AB}}{{T}_{BC}}=\dfrac{\sqrt{3}mg}{mg}=\dfrac{\sqrt{3}}{1} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
4．如图甲所示，两薄木板 $ A $ 、 $ B $ 质量相同，其中木板 $ A $ 与墙面间的动摩擦因数为 $ {\mu }_{1} $ ，木板 $ B $ 与木板 $ A $ 间的动摩擦因数为 $ {\mu }_{2} $ ，光滑重球被轻质细绳跨过定滑轮拉住，整个系统处于静止状态.现缓缓释放细绳使重球缓慢下降，对可能出现的情况，下列说法正确的是（ ）
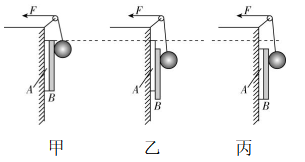
A．若出现图乙所示情况，只要 $ {\mu }_{1} > {\mu }_{2} $
B．若 $ {\mu }_{1} < 2{\mu }_{2} $ ，会出现图乙所示情况
C．要出现图丙所示情况，必有 $ {\mu }_{1}=2{\mu }_{2} $
D．若 $ {\mu }_{1} < 2{\mu }_{2} $ ，会出现图丙所示情况
设重球对木板 $ B $ 的压力为 $ F $ ,则对题图乙所示情况,对 $ A $ 分析可知 $ {\mu }_{1}F > {\mu }_{2}F+mg $ ,对 $ B $ 分析可知 $ {\mu }_{2}F < mg $ ,联立解得 $ {\mu }_{1} > 2{\mu }_{2} $ , $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误；对题图丙所示情况,对 $ A $ 、 $ B $ 整体分析可知 $ {\mu }_{1}F < 2mg $ ,对 $ B $ 分析可知 $ {\mu }_{2}F⩾ mg $ ,联立解得 $ {\mu }_{1} < 2{\mu }_{2} $ , $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
5．用三根细线 $ a $ 、 $ b $ 、 $ c $ 将质量均为 $ m $ 的小球1和2连接并悬挂，如图所示.两个小球处于静止状态，细线 $ a $ 与竖直方向的夹角为 $ {30}^{\circ } $ ，细线 $ c $ 水平，重力加速度为 $ g $ ，下列说法正确的是（ ）
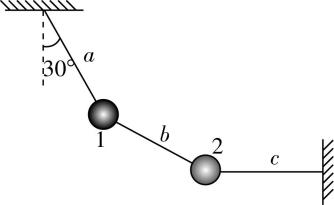
A．细线 $ a $ 上的张力大小为 $ 4mg $
B．细线 $ c $ 上的张力大小为 $ 2mg $
C．细线 $ b $ 上的张力大小为 $ \dfrac{\sqrt{21}}{3}mg $
D．细线 $ b $ 与竖直方向夹角的正切值 $ \tan \theta =\dfrac{\sqrt{3}}{2} $
对1、2两小球整体受力分析可知 $ {T}_{a} \cos {30}^{\circ }=2mg $ , $ {T}_{c}={T}_{a} \sin {30}^{\circ } $ ,可得细线 $ a $ 和细线 $ c $ 的张力大小分别为 $ {T}_{a}=\dfrac{4\sqrt{3}mg}{3} $ , $ {T}_{c}=\dfrac{2\sqrt{3}mg}{3} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误；对球2受力分析可知 $ {T}_{b}=\sqrt{{\left(mg\right) ^ {2}}+{T}_{c}^{2}} $ , $ \tan \theta =\dfrac{{T}_{c}}{mg} $ ,可得细线 $ b $ 的张力大小和细线 $ b $ 与竖直方向夹角的正切值分别为 $ {T}_{b}=\dfrac{\sqrt{21}}{3}mg $ , $ \tan \theta =\dfrac{2\sqrt{3}}{3} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
1．如图所示，将6个完全相同且质量分布均匀的“ $ \mathrm{\frown} $ ”形物体叠放在水平地面上，每个物体的接触点均在底端和顶端，整个系统处于静止状态.将最下面一排每个物体左侧底端（即 $ A $ 、 $ B $ 、 $ C $ 点）对地面的压力大小记为 $ {F}_{A} $ 、 $ {F}_{B} $ 、 $ {F}_{C} $ ，则（ ）
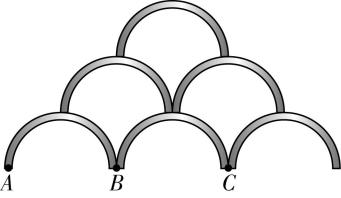
A． $ {F}_{A}:{F}_{B}:{F}_{C}=1:1:1 $
B． $ {F}_{A}:{F}_{B}:{F}_{C}=7:10:7 $
C． $ {F}_{A}:{F}_{B}:{F}_{C}=4:3:4 $
D． $ {F}_{A}:{F}_{B}:{F}_{C}=11:12:11 $
以上面两排物体为整体,则最下面一排物体对上面4个接触点的支持力大小为 $ 4F\prime =3mg $ ,可得 $ F\prime =\dfrac{3}{4}mg $ ,对最下面一排最左侧物体分析,由平衡条件及牛顿第三定律有 $ 2{F}_{A}=mg+F\prime $ ,可得 $ {F}_{A}=\dfrac{7}{8}mg $ ,同理,对最下面一排最右侧物体有 $ {F}_{C}=\dfrac{7}{8}mg $ ,对最下面一排中间物体有 $ 2{F}_{B}=mg+2F\prime $ ,解得 $ {F}_{B}=\dfrac{5}{4}mg $ ,则 $ {F}_{A}:{F}_{B}:{F}_{C}=7:10:7 $ , $ \mathrm{B} $ 正确.
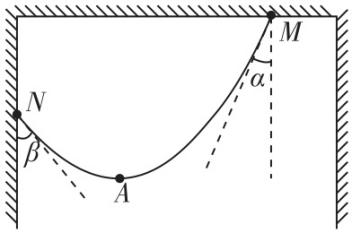
2．如图所示，支架上竖直悬挂着质量为 $ m=5\mathrm{k}\mathrm{g} $ 粗细均匀的金属细绳，悬点 $ M $ 、 $ N $ 处切线与竖直方向夹角分别为 $ \alpha ={37}^{\circ } $ 和 $ \beta ={53}^{\circ } $ ， $ A $ 点为最低点，已知 $ \cos {53}^{\circ }=0.6 $ ， $ \sin {53}^{\circ }=0.8 $ ，重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ，则（ ）
（多选）
A．悬点 $ M $ 对金属细绳的拉力大小为 $ 40\mathrm{N} $
B．悬点 $ N $ 对金属细绳的拉力大小为 $ 20\mathrm{N} $
C．最低点 $ A $ 处张力大小为 $ 15\mathrm{N} $
D． $ AN $ 段金属细绳的质量为 $ 1.8\mathrm{k}\mathrm{g} $
对金属细绳受力分析,受重力 $ mg $ 、悬点 $ M $ 对金属细绳拉力 $ {F}_{1} $ 、悬点 $ N $ 对金属细绳拉力 $ {F}_{2} $ ,则由平衡条件有 $ {F}_{1} \sin {37}^{\circ }={F}_{2} \sin {53}^{\circ } $ , $ {F}_{1} \cos {37}^{\circ }+{F}_{2} \cos {53}^{\circ }=mg $ ,联立解得 $ {F}_{1}=0.8mg=40\mathrm{N} $ , $ {F}_{2}=0.6mg=30\mathrm{N} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误；对 $ AN $ 段金属细绳受力分析,受重力 $ {m}_{1}g $ 、最低点 $ A $ 处张力 $ F $ 和悬点 $ N $ 对金属细绳拉力 $ {F}_{2} $ ,则 $ F={F}_{2} \sin {53}^{\circ }=0.48mg=24\mathrm{N} $ , $ {m}_{1}g={F}_{2} \cos {53}^{\circ }=0.36mg=18\mathrm{N} $ ,所以 $ AN $ 段金属细绳质量为 $ {m}_{1}=0.36m=1.8\mathrm{k}\mathrm{g} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
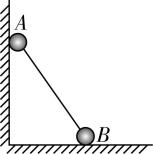
3．如图所示，两个质量都是 $ m $ 的小球 $ A $ 、 $ B $ 用轻杆连接后靠在墙上处于静止状态，已知墙面光滑，水平地面粗糙，重力加速度为 $ g $ .则下列说法正确的是（ ）
（多选）
A．小球 $ B $ 受到地面给它的支持力大小为 $ mg $
B．小球 $ A $ 和小球 $ B $ 受力个数之比为 $ 3:4 $
C．小球 $ A $ 受到竖直墙面给它的弹力大小与小球 $ B $ 受到的静摩擦力大小相等
D．当小球 $ A $ 的质量增加为 $ 2m $ 时，小球 $ B $ 对地面的压力大小不变
对 $ A $ 、 $ B $ 两个小球以及轻杆组成的整体进行受力分析,受到重力 $ 2mg $ 、地面的支持力 $ N $ 、竖直墙面水平向右的弹力 $ {F}_{\mathrm{N}} $ 以及地面水平向左的静摩擦力, $ A $ 、 $ B $ 两个小球以及轻杆整体静止靠在墙上,受力平衡,合外力为0,则小球 $ B $ 受到地面给它的支持力大小为 $ 2mg $ , $ \mathrm{A} $ 错误；由上述分析可知,整体处于平衡状态,则小球 $ A $ 受到墙面给它的弹力大小与小球 $ B $ 受到的静摩擦力大小相等,当小球 $ A $ 的质量增大为 $ 2m $ 时,系统对地面的压力增大,即小球 $ B $ 对地面的压力增大, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误；小球 $ A $ 受到重力、轻杆对小球 $ A $ 的弹力、竖直墙面对小球 $ A $ 水平向右的弹力,共三个力,小球 $ B $ 受到重力、水平地面对小球 $ B $ 的支持力、轻杆对小球 $ B $ 的弹力以及地面对小球 $ B $ 水平向左的静摩擦力,共四个力,故小球 $ A $ 和小球 $ B $ 受力个数之比为 $ 3:4 $ , $ \mathrm{B} $ 正确.
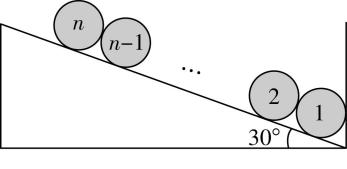
4．如图所示，一辆卡车卸货前，已经将车斗倾斜（倾角为 $ {30}^{\circ } $ ），有一挡板未撤下且处于竖直状态.车斗里装了 $ n $ 根钢管 $ (n > 3) $ ，钢管质量均为 $ m $ ，重力加速度为 $ g $ ，忽略钢管与车斗底面、挡板之间的摩擦，各钢管均处于静止状态.则下列说法中正确的是（ ）
（多选）
A．钢管1对挡板的弹力大小为 $ \dfrac{\sqrt{3}}{3}nmg $
B．钢管1对钢管2的弹力大小为 $ \dfrac{n-1}{2}mg $
C．钢管1对车斗底面的压力大小为 $ \dfrac{\sqrt{3}(n+3)}{3}mg $
D．若将挡板绕下端点缓慢顺时针转 $ {30}^{\circ } $ ，则转动过程中车斗底面对所有钢管的支持力均减小
以 $ n $ 根钢管为整体,由平衡条件可得,挡板对钢管1的弹力大小为 $ {F}_{挡}=nmg \tan {30}^{\circ }=\dfrac{\sqrt{3}}{3}nmg $ ,由牛顿第三定律可知钢管1对挡板的弹力大小为 $ \dfrac{\sqrt{3}}{3}nmg $ ,故 $ \mathrm{A} $ 正确；以除了钢管1外的所有钢管为整体,由平衡条件可得,钢管1对钢管2的弹力大小为 $ {N}_{12}=(n-1)mg \sin {30}^{\circ }=\dfrac{n-1}{2}mg $ ,故 $ \mathrm{B} $ 正确；对钢管1受力分析,在垂直车斗底面的方向上,由平衡条件可得 $ {N}_{斜}=mg \cos {30}^{\circ }+{F}_{挡} \sin {30}^{\circ }=\dfrac{\sqrt{3}(n+3)}{6}mg $ ,由牛顿第三定律可知钢管1对车斗底面的压力大小为 $ \dfrac{\sqrt{3}(n+3)}{6}mg $ ,故 $ \mathrm{C} $ 错误；若将挡板绕下端点缓慢顺时针转动 $ {30}^{\circ } $ ,则转动过程中车斗底面对除了钢管1外的其他钢管的支持力总是不变的,故 $ \mathrm{D} $ 错误.
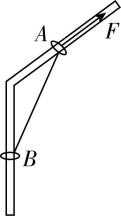
5．如图所示，一根弯折的光滑杆上套着两个小环 $ A $ 、 $ B $ ，小环 $ A $ 位于倾斜部分，小环 $ B $ 位于竖直部分，小环直径略大于杆，两小环用轻绳相连.小环 $ A $ 在沿杆向上的力 $ F $ 的作用下缓慢沿杆向上运动的过程中，下列说法正确的是（ ）
（多选）
A．杆对 $ B $ 环的弹力增大
B．轻绳上的张力会变大
C．力 $ F $ 变小
D．杆对 $ A $ 环的弹力变小
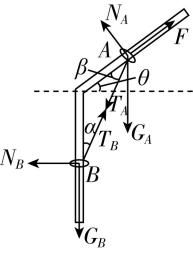
设绳与竖直杆的夹角为 $ \alpha $ ,与倾斜杆的夹角为 $ \beta $ ,倾斜杆与水平方向的夹角为 $ \theta $ .分别对 $ A $ 、 $ B $ 受力分析,如图所示.将绳对 $ B $ 的拉力正交分解,由平衡条件可得竖直杆的支持力和绳的拉力大小分别为 $ {N}_{B}={T}_{B} \sin \alpha $ , $ {T}_{B}=\dfrac{{G}_{B}}{ \cos \alpha } $ ,小环 $ A $ 在沿杆向上的力 $ F $ 的作用下缓慢沿杆向上运动的过程中, $ \alpha $ 增大,则 $ {T}_{B} $ 、 $ {N}_{B} $ 都变大,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 正确；对小环 $ A $ 受力分析,受到绳的拉力 $ {T}_{A}={T}_{B} $ ,倾斜杆的支持力 $ {N}_{A} $ ,重力 $ {G}_{A} $ 和 $ F $ ,由平衡条件可得 $ {T}_{A} \cos \beta +{G}_{A} \sin \theta =F $ ,随着小环 $ A $ 上移,夹角 $ \beta $ 逐渐减小,可知力 $ F $ 变大,故 $ \mathrm{C} $ 错误；对两个小环和轻绳整体受力分析,可得 $ {N}_{A}+{N}_{B} \sin \theta =({G}_{A}+{G}_{B}) \cos \theta $ , $ {N}_{B} $ 增大,因此 $ {N}_{A} $ 减小,故 $ \mathrm{D} $ 正确.
